Aufgabe Q3
Gegeben ist der Graph, der die kumulierten
Wahrscheinlichkeiten für eine
normalverteilte Zufallsgröße darstellt.
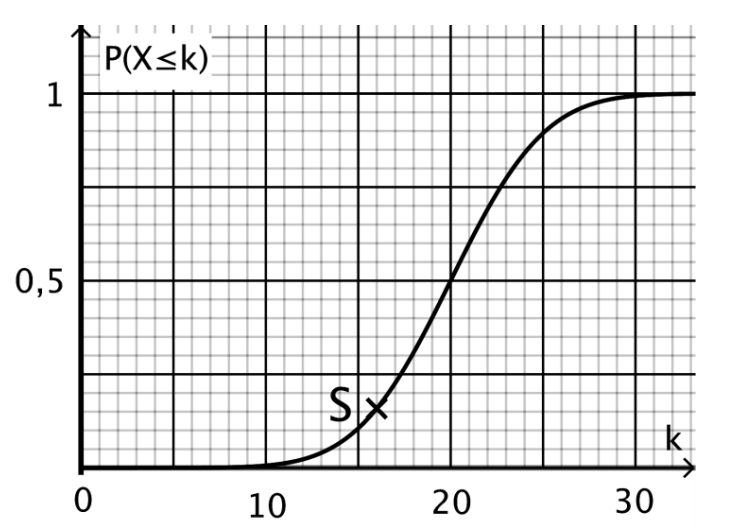
Begründen Sie, dass gilt: . [1 BE]
Der Punkt liegt auf dem Graphen und hat die Koordinaten .
Bestimmen Sie einen Näherungswert für . [4 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
serlo.orgDieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
→ Was bedeutet das?