Wahlteil - GTR - lernen mit Serlo!

Aufgabe 1A

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_{a}$ mit

$f_a(x) =\frac{1}{a^3}x^3 −\frac1ax^2 + x$ und $a\in\mathbb{R}^+$ .

Skizzieren Sie den Graphen von $f_{4}$ in Abbildung 1.
Geben Sie die Extrempunkte von $f_{4}$ an. [5BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Skizziere den Graphen von $f_{4}$ in Abbildung 1
$f_4(x)=\dfrac{1}{64}x^3-\dfrac{1}{4}x^2+x$
Gib die Extrempunkte von $f_{4}$ an
Lasse Dir den Graphen von $f_{4} (x)$ anzeigen und bestimme den Tiefpunkt.
$\Rightarrow\;TP(8|0)$
Der Tiefpunkt hat die Koordinaten $(8 ∣ 0)$ .
Für den Hochpunkt folgt: $x\approx2{,}66666...$ und $y\approx1{,}1851...$
$\Rightarrow\;HP\left(2{,}7|1{,}2\right)$
Der Hochpunkt hat etwa die Koordinaten $(2,7 ∣ 1,2)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Skizziere den Graphen von $f_{4} (x)$ .
Teil 2
Lasse Dir den Graphen von $f_{4} (x)$ anzeigen und bestimme den Tiefpunkt und den Hochpunkt.
Ermitteln Sie die Koordinaten der beiden gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{4}$ .
Die Graphen von $f_{1}$ und $f_{3}$ haben die beiden gemeinsamen Punkte $S_{1} (0 ∣ 0)$ und $S_{2} (s_{x} ∣ s_{y})$ mit $s_x \approx 0{,}69$ und $s_y \approx 0{,}54$ . Weisen Sie nach, dass es nur einen Punkt gibt, der auf allen Graphen der Schar liegt. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Ermittle die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{4}$
$f_{1}(x)=x^3-x^2+x$
Lasse Dir die Graphen von $f_{1} (x)$ und $f_{4} (x)$ anzeigen und bestimme ihre Schnittpunkte:
Man erhält die beiden Lösungen $x_{1} = 0$ und $f_{1} (0) = f_{4} (0) = 0$ , sowie
$x_2\approx0{,}761904...$ . und $f_1\left(0{,}761904...\right)=f_4\left(0{,}761904...\right)\approx0{,}623690...$
$\Rightarrow\;P_1(0|0)$ und $P_2(0{,}76|0{,}62)$
Die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{4}$ sind $(0 ∣ 0)$ und etwa $(0,76 ∣ 0,62)$ .
Die Graphen von $f_{1}$ und $f_{3}$ haben die beiden gemeinsamen Punkte $S_{1} (0 ∣ 0)$ und $S_{2} (s_{x} ∣ s_{y})$ mit $s_x \approx 0{,}69$ und $s_y \approx 0{,}54$ . Weise nach, dass es nur einen Punkt gibt, der auf allen Graphen der Schar liegt
Es gilt unabhängig von $a$ :
$f_{a} (0) = 0$
Wegen $s_x \neq x_2$ gibt es nur den Punkt $(0 ∣ 0)$ der auf allen Graphen der Funktionenschar liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Lasse Dir die Graphen von $f_{1} (x)$ und $f_{4} (x)$ anzeigen und bestimme ihre Schnittpunkte.
Teil 2
Welcher Funktionswert ist unabhängig von $a$ ?
Vergleiche $s_{x}$ mit $x_{2}$ .
Die Gleichung $f_{a} (x) = 0$ hat in Abhängigkeit von $a$ die Lösungen $\frac{a^2−\sqrt{a^3⋅(a−4)}}{2}$ und $0$ und $\frac{a^2+\sqrt{a^3⋅(a−4)}}{2}$ .
Geben Sie die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $𝑎$ an und begründen Sie Ihre Angabe anhand der obigen Terme. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Diskriminante
Gib die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $𝑎$ an und begründe Deine Angabe anhand der gegebenen Terme
Es gilt: $a\in\mathbb{R}^+$
Entscheidend für die Anzahl der Nullstellen ist der Wert der Diskriminante $D=a^3\cdot(a-4)$ in den beiden Termen $\frac{a^2\pm\sqrt{a^3⋅(a−4)}}{2}$ .
Für $a > 4$ ist $D>0\;\Rightarrow\; G_{f_a}$ hat $3$ Nullstellen.
Für $a = 4$ ist $D=0\;\Rightarrow\; G_{f_a}$ hat $2$ Nullstellen.
Für $a < 4$ ist $D<0\;\Rightarrow\; G_{f_a}$ hat $1$ Nullstelle.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Entscheidend für die Anzahl der Nullstellen ist der Wert der Diskriminante $D=a^3\cdot(a-4)$

Der Graph jeder Funktion $f_{a}$ hat genau einen Wendepunkt $(\frac {a^2}{3}|y_a)$ .

Bestimmen Sie den Wert von $𝑎$ zu dem Wendepunkt mit der größten y-Koordinate. [5 BE]

Für ein Umweltschutzprojekt nehmen zwei Unterwasserdrohnen $U 1$ und $U 2$ in einem See Messungen in unterschiedlichen Tiefen vor. Sie bewegen sich nur in vertikaler Richtung, d.h. senkrecht zur Wasseroberfläche des Sees. Ihre Geschwindigkeiten werden für $0 \le t \le 30$ durch die in $\mathbb{R}$ definierten Funktionen $v$ bzw. $w$ beschrieben, wobei gilt:
$v(t) = −\frac{6}{25}t \cdot (4t − 25) ⋅ e^{−\frac15\cdot t}$ und $w(t) =\frac{1}{216}t^3 −\dfrac{1}{6}t^2 + t$
Dabei ist $t$ die seit Beobachtungsbeginn vergangene Zeit in Minuten. $v (t)$ ist die
Geschwindigkeit von $U 1$ in Meter pro Minute und $w (t)$ ist die Geschwindigkeit von $U 2$ in Meter pro Minute. Wenn die Geschwindigkeit positiv ist, steigt die Unterwasserdrohne.
Bestimmen Sie die Koordinaten des Tiefpunktes des Graphen von $v$ und
interpretieren Sie die Werte im Sachkontext. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Bestimme die Koordinaten des Tiefpunktes des Graphen von $v$
Betrachte den Graphen von $v (t)$ und lasse Dir das Minimum anzeigen.
Der Tiefpunkt ist $T P (14 ∣ - 6,3)$ .
Die Koordinaten des Tiefpunktes des Graphen von $v$ sind etwa $(14 ∣ - 6,3)$ .
Interpretiere die Werte im Sachkontext
Etwa $14$ Minuten nach Beobachtungsbeginn beträgt die größte Sinkgeschwindigkeit von $U 1$ etwa $6{,}3 \;\dfrac{\text{m}}{\text{min}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte den Graphen von $v (t)$ und lasse Dir das Minimum anzeigen.
Zu der angegebenen Zeit nach Beobachtungsbeginn hat $U 1$ die größte Sinkgeschwindigkeit.
Mit $v^{'}$ wird die erste Ableitungsfunktion von $v$ bezeichnet. Innerhalb eines bestimmten
Zeitraums gilt für jeden Zeitpunkt $t$ die folgende Aussage: $v (t) < 0$ und $v^{'} (t) > 0$
Interpretieren Sie dies in Bezug auf die Bewegung von $U 1$ in diesem Zeitraum. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Die momentane Änderungsrate - Ganz mathematisch!
Interpretiere die Aussage: $v (t) < 0$ und $v^{'} (t) > 0$ in Bezug auf die Bewegung von $U 1$ in diesem Zeitraum
Wegen $v (t) < 0$ sinkt $U 1$ . Wegen $v^{'} (t) > 0$ ist die momentane Änderungsrate
der Geschwindigkeit von $U 1$ positiv. Also sinkt $U 1$ in diesem Zeitraum immer
langsamer.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Was bedeutet $v (t) < 0$ und was bedeutet $v^{'} (t) > 0$ in Bezug auf die Bewegung von $U 1$ ?
Im Beobachtungszeitraum beträgt der geringste Abstand von $U 1$ zur Wasseroberfläche
des Sees $10$ Meter.
Ermitteln Sie den Abstand von $U 1$ zur Wasseroberfläche zu Beobachtungsbeginn. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Integral
Ermittle den Abstand von $U 1$ zur Wasseroberfläche zu Beobachtungsbeginn
$v(t) = −\frac{6}{25}t \cdot (4t − 25) ⋅ e^{−\frac15\cdot t}$
Betrachte den Term $4 t - 25$ .
Für $t>\dfrac{25}{4}=6{,}25$ ist der Term größer null und wegen des Minuszeichens am Anfang ist dann $v (t) < 0$ .
Für $t < 6,25$ ist der Term kleiner null und wegen des Minuszeichens am Anfang ist dann $v (t) > 0$ .
Somit gilt: $v (t) > 0$ für $0 < t < 6,25$ und $v (t) < 0$ für $6,25 < t < 30$ .
$U 1$ hat somit $6,25$ Minuten nach Beobachtungsbeginn den kleinsten Abstand
zur Wasseroberfläche.
Im Beobachtungszeitraum beträgt der geringste Abstand von $U 1$ zur Wasseroberfläche des Sees $10$ Meter. Dann berechnet sich der Abstand von $U 1$ zur Wasseroberfläche zu Beobachtungsbeginn in Metern:
Der Abstand von $U 1$ zur Wasseroberfläche zu Beobachtungsbeginn beträgt rund $31{,}7\;\text{m}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche, in welchem Zeitraum $v (t)$ größer bzw. kleiner $0$ ist. Zur Zeit $t_{x}$ , bei der sich das Vorzeichen von $v (t)$ ändert, hat $U 1$ den kleinsten Abstand zur Wasseroberfläche.
Der geringste Abstand von $U 1$ zur Wasseroberfläche des Sees beträgt $10$ Meter.
Zu Beobachtungsbeginn: $10+\displaystyle\int_0^{t_x}v(t)\;\mathrm{d}t$
$U_{2}$ ist zu Beobachtungsbeginn $5$ Meter tiefer als $U_{1}$ und steigt langsamer als $U_{1}$ .
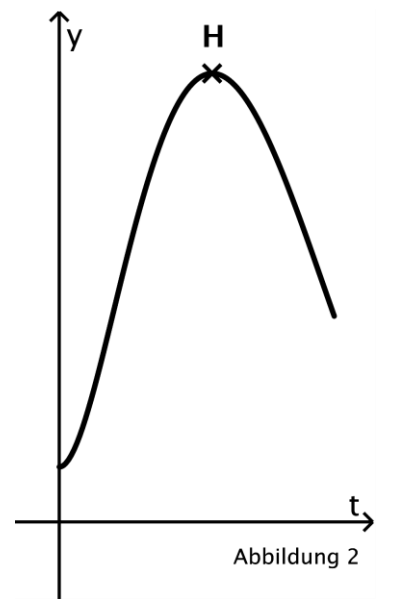
Der Graph in Abbildung 2 zeigt für die ersten Minuten des Beobachtungszeitraums die zeitliche Entwicklung des vertikalen Abstands der beiden Unterwasserdrohnen zueinander.
Im dargestellten Bereich hat der Graph nur einen Hochpunkt $H (t_{H} ∣ y_{H})$ .
Erläutern Sie, wie man $t_{H}$ anhand der Graphen von $v$ und $w$ ermitteln
kann, und geben Sie einen Term zur Berechnung von $y_{H}$ an. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Erläutere, wie man $t_{H}$ anhand der Graphen von $v$ und $w$ ermitteln kann
Bei der t-Koordinate $t_{s}$ des einzigen Schnittpunkts der Graphen von $v$ und $w$ innerhalb der ersten Minuten wechselt $w (t) < v (t)$ zu $v (t) < w (t)$ . Somit
nimmt der vertikale Abstand von $U 1$ und $U 2$ bis zum Zeitpunkt $t_{s}$ zu und danach
wieder ab. Folglich ist $t_{H} = t_{s}$ .
Gib einen Term zur Berechnung von $y_{H}$ an
$U_{2}$ ist zu Beobachtungsbeginn $5$ Meter tiefer als $U_{1}$ .
$\Rightarrow\;y_H = 5 + \displaystyle\int_0^{t_s}(v(t)-w(t))\;\mathrm{d}t$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Innerhalb der ersten Minuten gibt es einen Schnittpunkt der Graphen von $v$ und $w$ .
Was passiert zu diesem Zeitpunkt?
Beachte: $U_{2}$ ist zu Beobachtungsbeginn $5$ Meter tiefer als $U_{1}$ .

$\displaystyle f_a(x)$	$=$	$\displaystyle \frac{1}{a^3}x^3 −\frac1ax^2 + x$
	↓	Setze $x=\dfrac{a^2}{3}$ ein.
	$=$	$\displaystyle \dfrac{1}{a^3}\left(\dfrac{a^2}{3}\right)^3 −\dfrac1a\left(\dfrac{a^2}{3}\right)^2 + \dfrac{a^2}{3}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{1}{a^3}\cdot\dfrac{a^6}{27}−\dfrac1a\cdot\dfrac{a^4}{9} + \dfrac{a^2}{3}$
	↓	Kürze.
	$=$	$\displaystyle \dfrac{a^3}{27}-\dfrac{a^3}{9}+\dfrac{a^2}{3}$
	↓	Fasse zusammen.
	$=$	$\displaystyle -\dfrac{2}{27} a^3+\dfrac{1}{3}\cdot a^2$

Aufgabe 1A

Skizziere den Graphen von f4f_4f4​ in Abbildung 1

Gib die Extrempunkte von f4f_4f4​ an

Hast du eine Frage oder Feedback?

Ermittle die Koordinaten der gemeinsamen Punkte der Graphen von f1f_1f1​ und f4f_4f4​

Hast du eine Frage oder Feedback?

Gib die Anzahl der Nullstellen von faf_afa​ in Abhängigkeit von 𝑎𝑎a an und begründe Deine Angabe anhand der gegebenen Terme

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten des Tiefpunktes des Graphen von vvv

Interpretiere die Werte im Sachkontext

Hast du eine Frage oder Feedback?

Interpretiere die Aussage: v(t)<0v(t) < 0v(t)<0 und v′(t)>0v'(t) > 0v′(t)>0 in Bezug auf die Bewegung von U1U1U1 in diesem Zeitraum

Hast du eine Frage oder Feedback?

Ermittle den Abstand von U1U1U1 zur Wasseroberfläche zu Beobachtungsbeginn

Hast du eine Frage oder Feedback?

Erläutere, wie man tHt_HtH​ anhand der Graphen von vvv und www ermitteln kann

Gib einen Term zur Berechnung von yHy_HyH​ an

Hast du eine Frage oder Feedback?

Skizziere den Graphen von $f_{4}$ in Abbildung 1

Gib die Extrempunkte von $f_{4}$ an

Ermittle die Koordinaten der gemeinsamen Punkte der Graphen von $f_{1}$ und $f_{4}$

Gib die Anzahl der Nullstellen von $f_{a}$ in Abhängigkeit von $𝑎$ an und begründe Deine Angabe anhand der gegebenen Terme

Bestimme die Koordinaten des Tiefpunktes des Graphen von $v$

Interpretiere die Aussage: $v (t) < 0$ und $v^{'} (t) > 0$ in Bezug auf die Bewegung von $U 1$ in diesem Zeitraum

Ermittle den Abstand von $U 1$ zur Wasseroberfläche zu Beobachtungsbeginn

Erläutere, wie man $t_{H}$ anhand der Graphen von $v$ und $w$ ermitteln kann

Gib einen Term zur Berechnung von $y_{H}$ an