Teil 2, Analysis II - lernen mit Serlo!

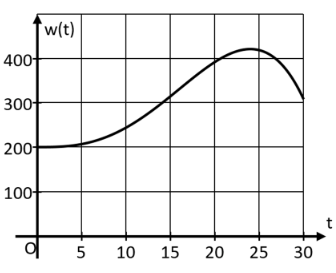
Das Landesamt für Umwelt ist unter anderem dafür zuständig, vor Überflutungen durch Flüsse zu warnen und lässt dazu täglich kontinuierlich die Wasserstände diverser Flüsse überprüfen. Der Wasserstand eines bestimmten Flusses im März des Jahres 2010 kann vereinfacht durch die Funktion $w$ mit der Funktionsgleichun $w (t) = a t^{4} + b t^{3} + c$ mit geeigneten Werten $a,b,c\in\mathbb{R}$ und der Definitionsmenge $D_{w} = [0; 30]$ beschrieben werden. Dabei bedeutet die Variable $t$ die Zeit in Tagen ab Monatsbeginn zum Zeitpunkt $t_{0} = 0$ . Der Funktionswert $w (t)$ gibt den Wasserstand des Flusses in $cm$ an. Zu Monatsbeginn lag der Wasserstand bei $200 \cm$ und am Monatsende bei $308 \cm$ . Der höchste Wasserstand wurde am 25. März – also zum Zeitpunkt $t_{max}=24$ – gemessen. Der abgebildete Graph zeigt den Wasserstand $w (t)$ in Abhängigkeit von der Zeit $t$ .

Auf das Mitführen von Einheiten während der Rechnungen kann verzichtet werden. Runden Sie Ihre Ergebnisse – falls nicht anders gefordert – sinnvoll.

Bestimmen Sie die Werte der Parameter $a, b$ und $c$ und damit die zugehörige Funktionsgleichung von $w$ .
[Mögliches Ergebnis: $w(t)=-\dfrac{1}{500}(t^4-32t^3-100000)$ ]
Berechnen Sie den höchsten Pegel im Beobachtungszeitraum zentimetergenau.
Ermitteln Sie rechnerisch das Datum im Beobachtungszeitraum, an dem die Änderungsgeschwindigkeit des Pegelstandes am größten war.
Berechnen Sie $\displaystyle\dfrac{1}{30}\int_0^{30} w(t)\operatorname{d}\!t$ und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik.