Ein Designstudio hat eine Nachttischleuchte entworfen. Diese besteht aus einem halbkugelförmigen Schirm mit Radius und einem Leuchtenfuß in der Form eines geraden Kreiskegels mit der Höhe und dem Durchmesser in der Grundfläche (siehe Skizze). Bei Berechnungen kann auf die Verwendung von Einheiten verzichtet werden.
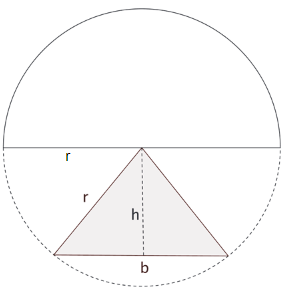
Bestimmen Sie die Maßzahl des Volumens des Fußes der Leuchte in Abhängigkeit von .
[Mögliches Ergebnis: ]
Aus technischen Gründen wird für die Funktion als Definitionsbereich gewählt. Bestimmen Sie die Höhe des Leuchtenfußes so, dass die Maßzahl seines Volumens den absolut größten Wert annimmt. Nach Auffassung der Designer würde dann die Leuchte die ansprechendsten Proportionen besitzen.
