A II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Der Graph $G_{f}$ einer ganzrationalen Funktion $f$ vierten Grades mit $D_f=\mathbb{R}$ ist symmetrisch zur $y -$ Achse und hat einen Wendepunkt $W_{1} (1 ∣ 2, 5)$ . Die Tangente $G_{t}$ im Punkt $W_{1}$ besitzt die Gleichung $t : y = 4 x - 1, 5$ mit $x\in \mathbb{R}.$
1. Bestimmen Sie den Funktionsterm $f (x)$ . [Mögliches Ergebnis: $f(x)=\dfrac{1}{2}(x^4-6x^2)$ ]
2. Ermitteln Sie sämtliche Nullstellen der Funktion $f$ und deren Vielfachheit. Erklären Sie die Bedeutung der Vielfachheit dieser Nullstellen für den Graphen $G_{f}$ .
3. Bestimmen Sie die maximalen Monotonieintervalle der Funktion $f$ sowie Art und Koordinaten der relativen Extrempunkte des Graphen $G_{f}$ .
4. Begründen Sie ohne weitere Rechnung, dass der Graph $G_{f}$ genau zwei Wendepunkte besitzt und geben Sie die Koordinaten des zweiten Wendepunkts an. Berechnen Sie auch die $x$ -Koordinaten sämtlicher Punkte von $G_{f}$ , welche die gleichen $y$ -Koordinaten wie die Wendepunkte haben.
5. Zeichnen Sie unter Mitverwendung vorliegender Ergebnisse den Graphen $G_{f}$ im Bereich $-2{,}5\le x\le 2{,}5$ in ein kartesisches Koordinatensystem. Für weitere Teilaufgaben wird auf der $y$ -Achse der Bereich $-5\le y\le 5$ benötigt.
  Maßstab: 1 LE = $1 \cm$ .
6. Zeigen Sie, dass an der Stelle $x = - 2$ die Gleichung $f (x) - f^{'} (x) = 0$ gilt und bestimmen Sie alle weiteren Stellen mit dieser Eigenschaft. Erklären Sie, was das Ergebnis für den Graphen $G_{f}$ bedeutet.
7. Geben Sie exakt die Nullstellen und die Extremstellen der ersten Ableitungsfunktion $f^{'}$ an und zeichnen Sie den Graphen $G_{f^{'}}$ im Bereich $-2\le x\le 2$ in das vorhandene Koordinatensystem mit Farbe ein.
8. Die Graphen $G_{f}$ und $G_{f^{'}}$ schließen ein endliches Flächenstück ein, das im II. und III. Quadranten des Koordinatensystems liegt. Markieren Sie dieses Flächenstück und berechnen Sie die Maßzahl seines Inhalts.
2
Begründen oder widerlegen Sie folgende Aussage: Ist der Graph $G_{h}$ einer ganzrationalen Funktion $h$ symmetrisch zur $y$ -Achse, dann ist der Graph $G_{h}$ der ersten Ableitungsfunktion punktsymmetrisch zum Ursprung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Zur Erinnerung: Eine ganzrationale Funktion (auch: Polynomfunktion) ist von der Form:
$f(x) = \color{#cc0000}{a_n} \cdot x^{\color{#009999}{n}}+ \color{#cc0000}{a_{n-1}}\cdot x^{\color{#009999}{{n-1}}}+…+\color{#cc0000}{a_2} \cdot x^{\color{#009999}{2}}+\color{#cc0000}{{a_1}} \cdot x+\color{#cc0000}{a_0}$
Begründung der Aussage
Die Aussage ist wahr. Eine mögliche Begründung hierfür funktioniert wie folgt:
Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch zur
$y$ -Achse, wenn alle vorkommenden Exponenten gerade sind. Wenn du das noch nicht wusstest, dann hilft dir der Artikel zur Symmetrie von Graphen. Es gilt also:
Ist $\mathbf{G_h}$ achsensymmetrisch zur y-Achse, dann sind alle Exponenten von h gerade.
Beim Ableiten einer ganzrationalen Funktion verringert sich jeder Exponent um $1$ und der Term $a_{0}$ fällt weg. Wenn du das noch nicht wusstest, hilft dir der Artikel zum Ableiten von Potenzfunktionen. Daraus folgt:
Sind alle Exponenten von $\mathbf{h}$ gerade, so sind alle Exponenten von $\mathbf{h'}$ ungerade.
(Denn eine gerade Zahl minus eine ungerade Zahl ist wieder eine ungerade Zahl. Und die $1$ ist ungerade).
Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch zum Ursprung, wenn alle vorkommenden Exponenten ungerade sind. Wenn du das noch nicht wusstest, hilft dir ebenfalls der Artikel zur Symmetrie von Graphen. Also gilt folgendes:
Sind alle Exponenten von $\mathbf{h'}$ ungerade, so ist $\mathbf{G_{h'}}$ punktsymmetrisch zum Ursprung
Also gilt: Ist $G_{h}$ achsensymmetrisch zur $y$ -Achse, so ist $G_{h^{'}}$ punktsymmetrisch zum Ursprung. Das war zu zeigen.
3
Ein Designstudio hat eine Nachttischleuchte entworfen. Diese besteht aus einem halbkugelförmigen Schirm mit Radius $r=12\cm$ und einem Leuchtenfuß in der Form eines geraden Kreiskegels mit der Höhe $h$ und dem Durchmesser $b$ in der Grundfläche (siehe Skizze). Bei Berechnungen kann auf die Verwendung von Einheiten verzichtet werden.
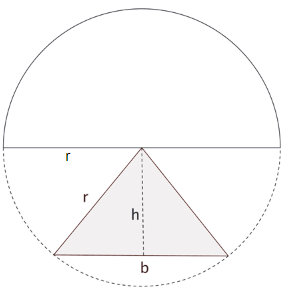
1. Bestimmen Sie die Maßzahl $V (h)$ des Volumens des Fußes der Leuchte in Abhängigkeit von $h$ .
  [Mögliches Ergebnis: $V(h=\dfrac{\pi}{3}(-h^3+144h)$ ]
2. Aus technischen Gründen wird für die Funktion $V:h\mapsto V(h)$ als Definitionsbereich $D_{V} = [2; 8]$ gewählt. Bestimmen Sie die Höhe $h$ des Leuchtenfußes so, dass die Maßzahl seines Volumens den absolut größten Wert annimmt. Nach Auffassung der Designer würde dann die Leuchte die ansprechendsten Proportionen besitzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?