Ein symmetrischer Trinkjoghurtbecher in der Form eines Fasses besitzt das Volumen . Hierbei ist jeweils der Durchmesser des Deckels und des Bodens und der maximale Durchmesser des Bechers auf halber Höhe (alle Längen in cm gemessen). Weiterhin soll % größer sein als . Der Becher soll so konstruiert sein, dass ein langer Strohhalm genau um aus dem Becher herausragt, wenn er diagonal im Becher liegt (siehe Abbildung).
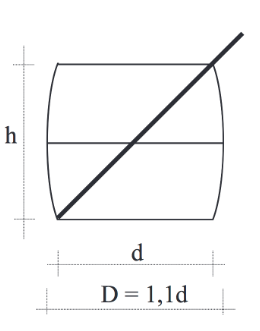
Stellen Sie eine Gleichung der Funktion auf, die die Maßzahl des Bechervolumens in Abhängigkeit von der Höhe beschreibt.
[Mögliches Ergebnis: ]
Mit der Vorgabe soll der Becher für eine kostenlose Probe das geringste Volu-men aufweisen. Berechnen Sie für diesen Fall die Höhe in und das zugehörige Volu-men in auf eine Nachkommastelle gerundet.
