A II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Gegeben ist die Funktion $f : x \mapsto \frac{3}{16} (x + 3) (x + \frac{4}{3}) (4 - x)$ mit $D_{f} = ℝ$ .
1. Bestimmen Sie die Nullstellen von $f$ und geben Sie das Verhalten der Funktionswerte $f (x)$ für $x \to - \infty$ und $x \to + \infty$ an.
2. Zeigen Sie, dass sich $f (x)$ auch in der Form $f (x) = - \frac{1}{16} (3 x^{3} + x^{2} - 40 x - 48)$ darstellen lässt.
3. Ermitteln Sie Art und Koordinaten der Extrempunkte des Graphen $G_{f}$ .
4. Zeichnen Sie den Graphen von $f$ im Bereich $- 4 \leq x \leq 4$ , auch unter Verwendung vorliegender Ergebnisse, in ein kartesisches Koordinatensystem. Maßstab: $1$ LE = $1 cm .$
5. Berechnen Sie die Steigung der Tangente an den Graphen $G_{f}$ im Schnittpunkt mit der $y$ -Achse. Bestimmen Sie dann den Bereich, in dem die Steigung des Graphen $G_{f}$ größer ist als die berechnete Tangentensteigung.
6. Die Parabel $P$ ist der Graph der quadratischen Funktion $p$ . $S (- 4 | 4)$ ist der Hochpunkt von $P$ und zugleich Schnittpunkt von $P$ mit $G_{f}$ . Ein weiterer Schnittpunkt der beiden Graphen liegt auf der $y$ -Achse. Ermitteln Sie den Funktionsterm von $p$ und zeichnen Sie die Parabel $P$ im Bereich $- 4 \leq x \leq 4$ in das Koordinatensystem ein.
  [Mögliches Teilergebnis: $p (x) = - \frac{1}{16} x^{2} - \frac{1}{2} x + 3$ ]
7. Die Graphen $G_{f}$ und $P$ schließen zwei Flächenstücke ein. Berechnen Sie die Maßzahl des Flächenstücks, das im II. und III. Quadranten des Koordinatensystems liegt.
2
Gegeben ist die Funktionenschar $g_{a} : x \mapsto 0,25 (x^{3} - 2 a x^{2})$ mit $x, a \in ℝ$ .
Der Graph von $g_{a}$ wird mit $G a$ bezeichnet.
1. Ermitteln Sie die Nullstellen von $g_{a}$ und geben Sie deren Vielfachheit in Abhängigkeit von $a$ an.
2. Nun wird $a = 3$ gesetzt und es gilt: $g_{3} (x) = 0,25 (x^{3} - 6 x^{2})$ . Des Weiteren ist die lineare Funktion $f : x \mapsto - 3 x + 2$ mit $x \in ℝ$ gegeben.
  1. Berechnen Sie die Koordinaten des Wendepunktes von $G_{3}$ .
  2. Untersuchen Sie rechnerisch, ob die abschnittsweise definierte
  Funktion
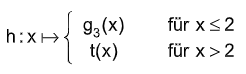
  an der Nahtstelle differenzierbar ist.
3. Beschreiben Sie mithilfe der Ergebnisse der letzten beiden Teilaufgaben die besondere Lage des Graphen der linearen Funktion $t$ in Bezug auf $G_{3}$ .
3
Ein symmetrischer Trinkjoghurtbecher in der Form eines Fasses besitzt das Volumen $V = \frac{1}{12} π \cdot h \cdot (2 D^{2} + d^{2})$ . Hierbei ist $d$ jeweils der Durchmesser des Deckels und des Bodens und $D$ der maximale Durchmesser des Bechers auf halber Höhe (alle Längen in cm gemessen). Weiterhin soll $D$ $10$ % größer sein als $d$ . Der Becher soll so konstruiert sein, dass ein $13 cm$ langer Strohhalm genau um $3 cm$ aus dem Becher herausragt, wenn er diagonal im Becher liegt (siehe Abbildung).
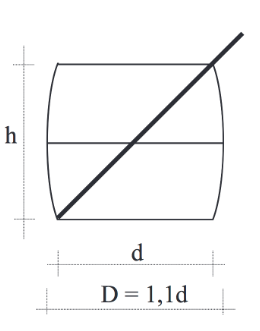
1. Stellen Sie eine Gleichung der Funktion $V$ auf, die die Maßzahl des Bechervolumens in Abhängigkeit von der Höhe $h$ beschreibt.
  [Mögliches Ergebnis: $V (h) = \frac{57}{200} π \cdot (- h^{3} + 100 h)$ ]
2. Mit der Vorgabe $5 \leq h \leq 9$ soll der Becher für eine kostenlose Probe das geringste Volu-men aufweisen. Berechnen Sie für diesen Fall die Höhe $h$ in $cm$ und das zugehörige Volu-men in ${cm}^{3}$ auf eine Nachkommastelle gerundet.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?