Das Volumen des Zylinders

Um das Volumen des Zylinders zu berechnen, braucht man den Flächeninhalt seiner Grundfläche und seine Höhe.

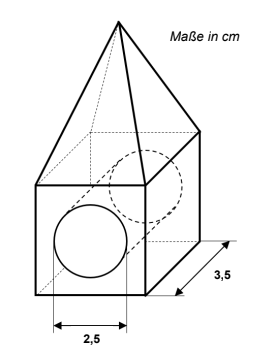
Der Zylinder ist so hoch wie der Würfel breit ist, also ist $h=\mathrm{3,5}\text{ cm}h\; =\; 3\{,\}5\; \backslash cm$.

Der Durchmesser des Zylinders ist ebenfalls gegeben, womit man den Radius berechnen kann:

$r=\mathrm{0,5}\cdot d=\mathrm{0,5}\cdot \mathrm{2,5}=\mathrm{1,25}r\; =\; 0\{,\}5\; \backslash cdot\; d\; =\; 0\{,\}5\; \backslash cdot\; 2\{,\}5\; =\; 1\{,\}25$

Mithilfe des Radius kann man jetzt den Flächeninhalt der Grundfläche berechnen:

$A_{\text{Grundfl}\ddot{\text{a}}\text{che}}=r^2\cdot \pi ={\mathrm{1,25}}^2\cdot \pi =\mathrm{1,5625}\cdot \pi A\_\{\backslash text\{Grundfläche\}\}\; =\; r^2\; \backslash cdot\; \backslash pi\; =\; 1\{,\}25^2\; \backslash cdot\; \backslash pi\; =\; 1\{,\}5625\; \backslash cdot\; \backslash pi$

Die Grundfläche hat also einen Flächeninhalt von $\mathrm{1,5625}\cdot \pi {\text{ cm}}^{2}1\{,\}5625\; \backslash cdot\; \backslash pi\; \backslash cm^2$.

Diesen Wert multipliziert man nun mit der Höhe des Zylinders:

$\mathrm{1,5625}\cdot \pi \cdot \mathrm{3,5}\approx \mathrm{17,18}1\{,\}5625\; \backslash cdot\; \backslash pi\; \backslash cdot\; 3\{,\}5\; \backslash approx\; 17\{,\}18$

Der Zylinder hat ein Volumen von ca. $\mathrm{17,18}{\text{ cm}}^{3}17\{,\}18\; \backslash cm^3$.

Das Volumen des Würfels

Um das Volumen des Würfels zu berechnen, multipliziert man einfach seine Länge, Höhe und Breite miteinander.

Da es sich um einen Würfel handelt, sind alle drei Werte gleich, nämlich $\mathrm{3,5}\text{ cm}3\{,\}5\; \backslash cm$.

$\mathrm{3,5}\cdot \mathrm{3,5}\cdot \mathrm{3,5}=\mathrm{42,875}3\{,\}5\; \backslash cdot\; 3\{,\}5\; \backslash cdot\; 3\{,\}5\; =\; 42\{,\}875$

Der Würfel hat ein Volumen von $\mathrm{42,875}{\text{ cm}}^{3}42\{,\}875\; \backslash cm^3$.

Das Volumen der Pyramide

6Um das Volumen der Pyramide zu berechnen, braucht man den Flächeninhalt der Grundfläche der Pyramide und ihre Höhe.

Um die Höhe der Pyramide zu ermitteln, subtrahiert man die Höhe des Würfels von der Gesamthöhe der Figur:

$\mathrm{7,5}-\mathrm{3,5}=47\{,\}5\; -\; 3\{,\}5\; =\; 4$

Die Pyramide ist also $4\text{ cm}4\; \backslash cm$ hoch.

Die Grundfläche ist so groß wie eine der Seiten des Würfels.

$\mathrm{3,5}\cdot \mathrm{3,5}=\mathrm{12,25}3\{,\}5\; \backslash cdot\; 3\{,\}5\; =\; 12\{,\}25$

Die Grundfläche der Pyramide hat einen Flächeninhalt von $\mathrm{12,25}{\text{ cm}}^{2}12\{,\}25\; \backslash cm^2$.

Jetzt setzt man die errechneten Werte in die Formel für das Volumen einer Pyramide ein:

$V_{\text{Pyramide}}=\frac{1}{3}\cdot G\cdot h=\frac{1}{3}\cdot \mathrm{12,25}\cdot 4=16,\bar{3}\approx \mathrm{16,33}V\_\{\backslash text\{Pyramide\}\}\; =\; \backslash frac\{1\}\{3\}\; \backslash cdot\; G\; \backslash cdot\; h\; =\; \backslash frac\{1\}\{3\}\; \backslash cdot\; 12\{,\}25\; \backslash cdot\; 4\; =\; 16,\backslash overline\{3\}\; \backslash approx\; 16\{,\}33$

Die Pyramide hat also ein Volumen von ca. $\mathrm{16,33}{\text{ cm}}^{3}16\{,\}33\; \backslash cm^3$.

Das Volumen der Figur

Das Volumen der Figur setzt sich zusammen aus dem Volumen des Würfels und der Pyramide, minus dem Volumen des Zylinders.

$V_{\text{Figur}}=V_{\text{W}\ddot{\text{u}}\text{rfel}}+V_{\text{Pyramide}}-V_{\text{Zylinder}}=\mathrm{42,875}+\mathrm{16,33}-\mathrm{17,18}=\mathrm{42,025}V\_\{\backslash text\{Figur\}\}\; =\; V\_\backslash text\{Würfel\}\; +\; V\_\backslash text\{Pyramide\}\; -\; V\_\backslash text\{Zylinder\}\; =\; 42\{,\}875\; +\; 16\{,\}33\; -\; 17\{,\}18\; =\; 42\{,\}025$

Die Figur hat ein Volumen von $\mathrm{42,025}{\text{ cm}}^{3}42\{,\}025\; \backslash cm^3$.