B3 Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Der Körper ist Teil eines mathematischen Modells eines Architekturbüros zur Planung eines neuen Hotels, das aus drei Gebäuden bestehen soll, die jeweils die gleiche Form besitzen (siehe Abbildung 2). Durch den Körper wird Gebäude I modelliert, die Gebäude II und III sind gegenüber Gebäude I jeweils um gedreht. Alle drei Gebäude stehen so aneinander, dass sie einen dreieckigen Innenhof bilden. In der Modellierung liegt dieser Innenhof in der -Ebene.
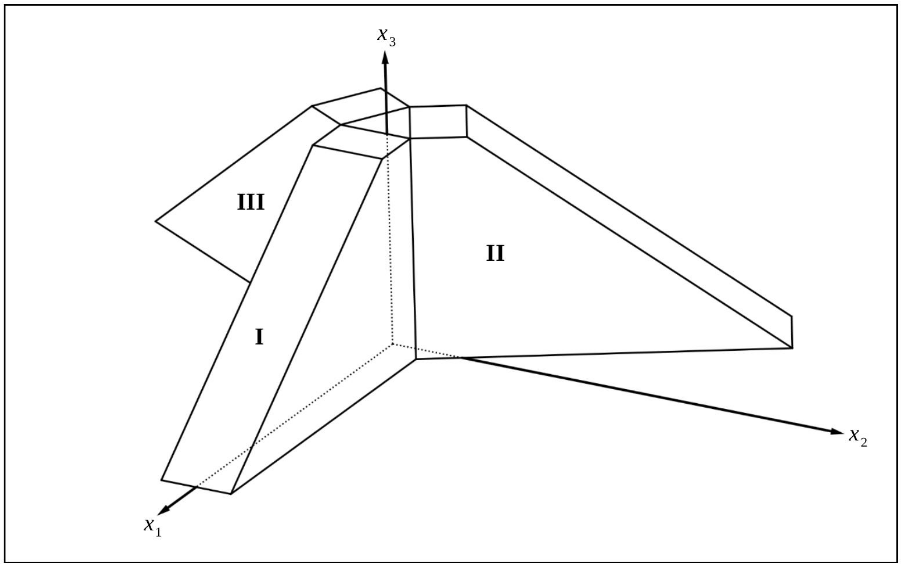
Abbildung 2
Die nebenstehende Abbildung 3 zeigt das Modell des Hotels von oben.
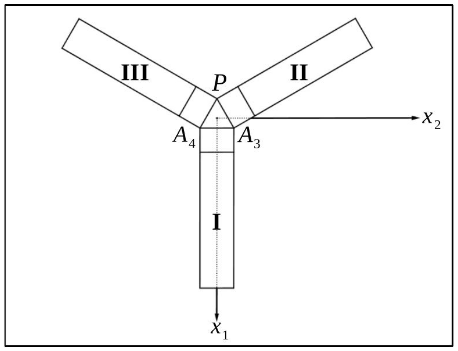
Abbildung 3
Der Innenhof hat die Form eines gleichseitigen Dreiecks.
Ermitteln Sie rechnerisch die Koordinaten des Punktes .
[Zur Kontrolle: (4 P)
Berechnen Sie den Abstand von zum Koordinatenursprung . (2 P)
