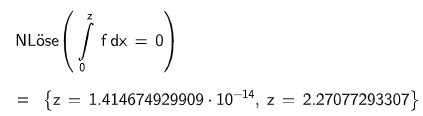B1 - lernen mit Serlo!

Aufgabe 2

Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.

Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = (x^{3} - 5) \cdot e^{x}, x \in ℝ$ .

Zwischen dem Graphen der Funktion $f$ und der $x$ -Achse liegt im 3. und 4. Quadranten eine Fläche mit endlichem Flächeninhalt, die nach links unendlich ausgedehnt ist.

Diese Fläche ist in Abbildung 2 schraffiert dargestellt.

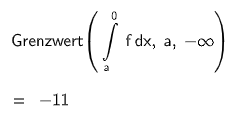
(i) Bestimmen Sie den Inhalt dieser Fläche gerundet auf drei Nachkommastellen.
(1 P + 2 P)
(ii) Die $y$ -Achse teilt diese Fläche in zwei Teilflächen.
Ermitteln Sie das Verhältnis der zugehörigen Flächeninhalte. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
(i) Bestimme den Inhalt dieser Fläche, gerundet auf drei Nachkommastellen
Berechne zunächst die Nullstelle der Funktion $f$ :
$f (x = 0 \Rightarrow 0 = (x^{3} - 5) \cdot e^{x} \Rightarrow$ wegen $e^{x} > 0$ folgt $x_{N} = \sqrt[3]{5}$ .
Berechne nun das Integral von $- \infty$ bis $x_{N}$ :
Es ist also $\lim_{a \to - \infty} \int_{a}^{\sqrt[3]{5}} f (x) d x \approx - 24,947$ .
Der Flächeninhalt beträgt ungefähr $24,947 FE$ .
(ii) Ermittele das Verhältnis der zugehörigen Flächeninhalte
Die $y$ -Achse teilt diese Fläche in zwei Teilflächen.
Berechne für die linke Fläche das Integral von $- \infty$ bis $0$ :
Der Flächeninhalt der linken Fläche ist gleich $11 FE$ .
Der Flächeninhalt der rechten Fläche ist gleich der Differenz der Gesamtfläche minus dem Flächeninhalt der linken Fläche $\Rightarrow 24,947 - 11 = 13,947$ .
Das Verhältnis der Flächeninhalte ist dann ungefähr $11 : 13,947 \approx 1 : 1,268$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
(i)
Berechne die Nullstelle der Funktion $f$ $\Rightarrow x_{N}$ .
Berechne das Integral von $- \infty$ bis $x_{N}$ (benutze dafür den $\lim$ ).
(ii)
Berechne für die linke Fläche das Integral von $- \infty$ bis $0$ (benutze dafür den $\lim$ ).
Der Flächeninhalt der rechten Fläche ist gleich der Differenz der Gesamtfläche minus dem Flächeninhalt der linken Fläche.
Berechne das Verhältnis der beiden Flächeninhalte.
Für $z \neq 0$ hat die Gleichung $\int_{0}^{z} f (x) d x = 0$ genau eine Lösung.
Bestimmen Sie diese Lösung und interpretieren Sie die Lösung geometrisch.
(2 P + 3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Bestimme diese Lösung
Löse die Gleichung $\int_{0}^{z} f (x) d x = 0$ .
Der Taschenrechner liefert: $z \approx 2,271$ .
(Der zweite angegebene Wert ist $z = 0$ , entfällt hier.)
Interpretiere die Lösung geometrisch
Das Flächenstück, das der Graph von $f$ mit den Koordinatenachsen unterhalb der x-Achse im 4. Quadranten einschließt, ist genauso groß wie das Flächenstück oberhalb der $x$ -Achse, das im Bereich von $x = \sqrt[3]{5}$ bis $x \approx 2,271$ zwischen dem Graphen von $f$ und der $x$ -Achse liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Löse die Gleichung $\int_{0}^{z} f (x) d x = 0$ .
Teil 2
Wenn die Flächenbilanz den Wert null hat, dann gibt es ein Flächenstück unterhalb der x-Achse, das genauso groß ist wie das Flächenstück oberhalb der $x$ -Achse.
Welche beiden Flächenstücke sind das?
Die Punkte $O (0 | 0), N (- 5 | 0), Y (0 | - 5)$ bilden ein Dreieck $O N Y$ . Der Graph der Funktion $f$ verläuft teilweise innerhalb des Dreiecks und schließt mit der Seite $N Y$ eine Fläche $A$ ein.
(i) Zeichnen Sie die Fläche $A$ in Abbildung 3 ein. (2 P)
[Hinweis: Abbildung 3 ist identisch mit Abbildung 1.]
(ii) Bestimmen Sie den Flächeninhalt der Fläche $A$ . (4 P)
(iii) Ermitteln Sie die beiden Punkte auf dem Graphen von $f$ , in denen die Tangente parallel zur Seite $N Y$ verläuft. (3 P)
Abbildung 3
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
(i) Zeichne die Fläche $A$ in Abbildung 3 ein
Abbildung 3
(ii) Bestimme den Flächeninhalt der Fläche $A$
Die Seite $N Y$ ist Teil der Geraden mit der Gleichung $y = - x - 5$ .
Für die Schnittstelle mit dem Graphen von $f$ liefert der Taschenrechner für $x < 0$ nur $x \approx - 3,582$ .
Für den Flächeninhalt folgt daraus: $\int_{- 3,582}^{0} (f (x) - (- x - 5)) d x \approx 3,748$ .
Der Flächeninhalt der Fläche $A$ beträgt rund $3,748 FE$ .
(iii) Ermittele die beiden Punkte auf dem Graphen von $f$ , in denen die Tangente parallel zur Seite $N Y$ verläuft
In den Berührpunkten muss die Steigung des Graphen mit der Steigung der Geraden übereinstimmen.
Die Seite $N Y$ ist Teil der Geraden mit der Gleichung $y = - x - 5$ , d.h. die Geradensteigung ist gleich $- 1$ .
Löse die Gleichung $f^{'} (x) = - 1$ .
Der Taschenrechner liefert für die Gleichung $f^{'} (x) = - 1$ die Lösungen $x_{B 1}$ und $x_{B 2}$ mit $x_{B 1} \approx - 1,049$ und $x_{B 2} \approx 1,070$ .
Berechne $f (x_{B 1})$ und $f (x_{B 2})$ :
Mit $f (x_{B 1}) \approx - 2,156$ und $f (x_{B 2}) \approx - 11,005$ ergeben sich die beiden gesuchten Punkte ungefähr zu $B_{1} (- 1,049 | - 2,156)$ und $B_{2} (1,070 | - 11,005)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
(i)
Zeichne die Punkte $N$ und $Y$ in die Abbildung ein. Verbinde die Punkte $N$ und $Y$ mit einer Strecke.
Diese Strecke schneidet den Graphen von $f$ .
Kennzeichne die entstandene Fläche.
(ii)
Die Seite $N Y$ ist Teil einer Geraden $g$ .
Bestimme die Geradengleichung $g (x)$ .
Für die Schnittstelle mit dem Graphen von $f$ liefert der Taschenrechner für $x < 0$ nur den Wert $x_{1}$ .
Berechne den Flächeninhalt: $\int_{x_{1}}^{0} (f (x) - g (x)) d x$ .
(iii)
In den Berührpunkten muss die Steigung des Graphen mit der Steigung der Geraden übereinstimmen $\Rightarrow m_{g}$ .
Löse die Gleichung $f^{'} (x) = m_{g} \Rightarrow x_{B 1}$ und $x_{B 2}$
Berechne $f (x_{B 1})$ und $f (x_{B 2})$ $\Rightarrow B_{1} (x_{B 1} | f (x_{B 1}))$ und $B_{2} (x_{B 2} | f (x_{B 2}))$ .