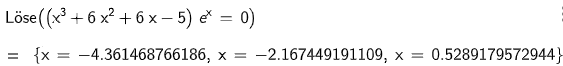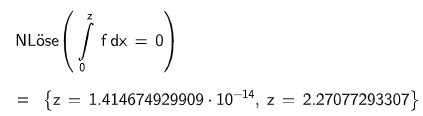B1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Die Funktion $f$ ist gegeben durch die Gleichung
$f (x) = (x^{3} - 5) e^{x}, x \in ℝ$ .
Der Graph von $f$ ist in Abbildung 1 dargestellt.
Abbildung 1
1. Berechnen Sie die Gleichung der Tangente an den Graphen von $f$ im Punkt $P (- 1 | f (- 1))$ , ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Berechne die Gleichung der Tangente an den Graphen von $f$ im Punkt $P (- 1 | f (- 1))$
  Gegeben ist $f (x) = (x^{3} - 5) e^{x}$ .
  Berechne $f^{'} (x)$ mit der Produktregel: $f^{'} (x) = 3 x^{2} \cdot e^{x} + (x^{3} - 5) \cdot e^{x} = (x^{3} + 3 x^{2} - 5) \cdot e^{x}$
  Für die Steigung der Tangente muss gelten: $m = f^{'} (- 1) = - 3 \cdot e^{- 1}$ .
  Berechne $f (- 1) = (- 1 - 5) \cdot e^{- 1} = - 6 \cdot e^{- 1}$ .
  Mit der Punktsteigungsform erhält man die Tangentengleichung:
  $y = - 3 \cdot e^{- 1} \cdot (x + 1) - 6 \cdot e^{- 1}$ oder $(y = - 3 \cdot e^{- 1} \cdot x - 9 \cdot e^{- 1})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{'} (x)$ .
  Für die Steigung der Tangente muss gelten: $m = f^{'} (- 1)$ .
  Berechne $f (- 1)$ .
  Mit der Punktsteigungsform erhält man die Tangentengleichung.
2. Der Graph von $f$ besitzt genau eine Extremstelle und drei Wendestellen.
  Berechnen Sie die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet
  Berechne $f^{''} (x)$ und löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
  $f^{'} (x) = (x^{3} + 3 x^{2} - 5) \cdot e^{x}$
  $\Rightarrow f^{''} (x) = (3 x^{2} + 6 x) \cdot e^{x} + (x^{3} + 3 x^{2} - 5) \cdot e^{x} = (x^{3} + 6 x^{2} + 6 x - 5) \cdot e^{x}$
  Löse die Gleichung $f^{''} (x) = 0$ :
  Die Gleichung hat die Lösungen $x_{W 1}, x_{W 2}$ und $x_{W 3}$ mit $x_{W 1} \approx - 4,361, x_{W 2} \approx - 2,167$ und $x_{W 3} \approx 0,529$ .
  Anmerkung: Da die Existenz von drei Wendestellen durch die Aufgabenstellung gesichert ist, ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
  Die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet sind
  $x_{W 1} \approx - 4,361, x_{W 2} \approx - 2,167$ und $x_{W 3} \approx 0,529$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{''} (x)$ und löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
  Hinweis: Es ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
3. Für $z > 0$ ist $P_{z} (z | f (z))$ ein Punkt auf dem Graphen von $f$ . Er bildet zusammen mit dem Koordinatenursprung $O (0 | 0)$ und dem Punkt $Q_{z} (z | 0)$ ein Dreieck $O P_{z} Q_{z}$ .
  Bestimmen Sie den Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
  Bestimme den Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird
  Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $T P (1,1 | - 11)$ .
  Dann erhält man für den Flächeninhalt des Dreiecks:
  $A_{Dreieck} = \frac{1}{2} \cdot g \cdot h \approx \frac{1}{2} \cdot 1,1 \cdot 11 = 6,05$ .
  Der Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird, beträgt rund $6,05 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $T P (x_{1} | y_{1})$ .
  Dann ist $A_{Dreieck} \approx \frac{1}{2} \cdot x_{1} \cdot y_{1}$ $[FE]$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = (x^{3} - 5) \cdot e^{x}, x \in ℝ$ .
Zwischen dem Graphen der Funktion $f$ und der $x$ -Achse liegt im 3. und 4. Quadranten eine Fläche mit endlichem Flächeninhalt, die nach links unendlich ausgedehnt ist.
Diese Fläche ist in Abbildung 2 schraffiert dargestellt.
Abbildung 2
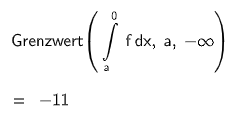
1. (i) Bestimmen Sie den Inhalt dieser Fläche gerundet auf drei Nachkommastellen.
  (1 P + 2 P)
  (ii) Die $y$ -Achse teilt diese Fläche in zwei Teilflächen.
  Ermitteln Sie das Verhältnis der zugehörigen Flächeninhalte. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  (i) Bestimme den Inhalt dieser Fläche, gerundet auf drei Nachkommastellen
  Berechne zunächst die Nullstelle der Funktion $f$ :
  $f (x = 0 \Rightarrow 0 = (x^{3} - 5) \cdot e^{x} \Rightarrow$ wegen $e^{x} > 0$ folgt $x_{N} = \sqrt[3]{5}$ .
  Berechne nun das Integral von $- \infty$ bis $x_{N}$ :
  Es ist also $\lim_{a \to - \infty} \int_{a}^{\sqrt[3]{5}} f (x) d x \approx - 24,947$ .
  Der Flächeninhalt beträgt ungefähr $24,947 FE$ .
  (ii) Ermittele das Verhältnis der zugehörigen Flächeninhalte
  Die $y$ -Achse teilt diese Fläche in zwei Teilflächen.
  Berechne für die linke Fläche das Integral von $- \infty$ bis $0$ :
  Der Flächeninhalt der linken Fläche ist gleich $11 FE$ .
  Der Flächeninhalt der rechten Fläche ist gleich der Differenz der Gesamtfläche minus dem Flächeninhalt der linken Fläche $\Rightarrow 24,947 - 11 = 13,947$ .
  Das Verhältnis der Flächeninhalte ist dann ungefähr $11 : 13,947 \approx 1 : 1,268$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Berechne die Nullstelle der Funktion $f$ $\Rightarrow x_{N}$ .
  Berechne das Integral von $- \infty$ bis $x_{N}$ (benutze dafür den $\lim$ ).
  (ii)
  Berechne für die linke Fläche das Integral von $- \infty$ bis $0$ (benutze dafür den $\lim$ ).
  Der Flächeninhalt der rechten Fläche ist gleich der Differenz der Gesamtfläche minus dem Flächeninhalt der linken Fläche.
  Berechne das Verhältnis der beiden Flächeninhalte.
2. Für $z \neq 0$ hat die Gleichung $\int_{0}^{z} f (x) d x = 0$ genau eine Lösung.
  Bestimmen Sie diese Lösung und interpretieren Sie die Lösung geometrisch.
  (2 P + 3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme diese Lösung
  Löse die Gleichung $\int_{0}^{z} f (x) d x = 0$ .
  Der Taschenrechner liefert: $z \approx 2,271$ .
  (Der zweite angegebene Wert ist $z = 0$ , entfällt hier.)
  Interpretiere die Lösung geometrisch
  Das Flächenstück, das der Graph von $f$ mit den Koordinatenachsen unterhalb der x-Achse im 4. Quadranten einschließt, ist genauso groß wie das Flächenstück oberhalb der $x$ -Achse, das im Bereich von $x = \sqrt[3]{5}$ bis $x \approx 2,271$ zwischen dem Graphen von $f$ und der $x$ -Achse liegt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Löse die Gleichung $\int_{0}^{z} f (x) d x = 0$ .
  Teil 2
  Wenn die Flächenbilanz den Wert null hat, dann gibt es ein Flächenstück unterhalb der x-Achse, das genauso groß ist wie das Flächenstück oberhalb der $x$ -Achse.
  Welche beiden Flächenstücke sind das?
3. Die Punkte $O (0 | 0), N (- 5 | 0), Y (0 | - 5)$ bilden ein Dreieck $O N Y$ . Der Graph der Funktion $f$ verläuft teilweise innerhalb des Dreiecks und schließt mit der Seite $N Y$ eine Fläche $A$ ein.
  (i) Zeichnen Sie die Fläche $A$ in Abbildung 3 ein. (2 P)
  [Hinweis: Abbildung 3 ist identisch mit Abbildung 1.]
  (ii) Bestimmen Sie den Flächeninhalt der Fläche $A$ . (4 P)
  (iii) Ermitteln Sie die beiden Punkte auf dem Graphen von $f$ , in denen die Tangente parallel zur Seite $N Y$ verläuft. (3 P)
  Abbildung 3
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  (i) Zeichne die Fläche $A$ in Abbildung 3 ein
  Abbildung 3
  (ii) Bestimme den Flächeninhalt der Fläche $A$
  Die Seite $N Y$ ist Teil der Geraden mit der Gleichung $y = - x - 5$ .
  Für die Schnittstelle mit dem Graphen von $f$ liefert der Taschenrechner für $x < 0$ nur $x \approx - 3,582$ .
  Für den Flächeninhalt folgt daraus: $\int_{- 3,582}^{0} (f (x) - (- x - 5)) d x \approx 3,748$ .
  Der Flächeninhalt der Fläche $A$ beträgt rund $3,748 FE$ .
  (iii) Ermittele die beiden Punkte auf dem Graphen von $f$ , in denen die Tangente parallel zur Seite $N Y$ verläuft
  In den Berührpunkten muss die Steigung des Graphen mit der Steigung der Geraden übereinstimmen.
  Die Seite $N Y$ ist Teil der Geraden mit der Gleichung $y = - x - 5$ , d.h. die Geradensteigung ist gleich $- 1$ .
  Löse die Gleichung $f^{'} (x) = - 1$ .
  Der Taschenrechner liefert für die Gleichung $f^{'} (x) = - 1$ die Lösungen $x_{B 1}$ und $x_{B 2}$ mit $x_{B 1} \approx - 1,049$ und $x_{B 2} \approx 1,070$ .
  Berechne $f (x_{B 1})$ und $f (x_{B 2})$ :
  Mit $f (x_{B 1}) \approx - 2,156$ und $f (x_{B 2}) \approx - 11,005$ ergeben sich die beiden gesuchten Punkte ungefähr zu $B_{1} (- 1,049 | - 2,156)$ und $B_{2} (1,070 | - 11,005)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Zeichne die Punkte $N$ und $Y$ in die Abbildung ein. Verbinde die Punkte $N$ und $Y$ mit einer Strecke.
  Diese Strecke schneidet den Graphen von $f$ .
  Kennzeichne die entstandene Fläche.
  (ii)
  Die Seite $N Y$ ist Teil einer Geraden $g$ .
  Bestimme die Geradengleichung $g (x)$ .
  Für die Schnittstelle mit dem Graphen von $f$ liefert der Taschenrechner für $x < 0$ nur den Wert $x_{1}$ .
  Berechne den Flächeninhalt: $\int_{x_{1}}^{0} (f (x) - g (x)) d x$ .
  (iii)
  In den Berührpunkten muss die Steigung des Graphen mit der Steigung der Geraden übereinstimmen $\Rightarrow m_{g}$ .
  Löse die Gleichung $f^{'} (x) = m_{g} \Rightarrow x_{B 1}$ und $x_{B 2}$
  Berechne $f (x_{B 1})$ und $f (x_{B 2})$ $\Rightarrow B_{1} (x_{B 1} | f (x_{B 1}))$ und $B_{2} (x_{B 2} | f (x_{B 2}))$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = (x^{3} - 5) \cdot e^{x}, x \in ℝ$ .
Gegeben ist die Schar der in $ℝ$ definierten Funktionen $f_{k}$ durch die Funktionsgleichung
$f_{k} (x) = (x^{3} + k) \cdot e^{x} mit k \in ℝ$ .
Die Funktion $f_{- 5}$ stimmt mit der Funktion $f$ überein.
Die folgende Abbildung 4 zeigt drei Graphen der Schar $G_{I}, G_{I I}, G_{I I I}$ für drei verschiedene Parameter $k_{I}, k_{I I}, k_{I I I}$ .
Abbildung 4
1. Geben Sie die zugehörigen Parameter an. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionenschar
  Gib die zugehörigen Parameter an
  Es ist $f_{k} (x) = (x^{3} + k) \cdot e^{x}$ .
  Bei Graph $G_{I}$ ist $f_{k} (0) = 2 \Rightarrow 2 = (0 + k) \cdot e^{0} \Rightarrow k = k_{I} = 2$ .
  Bei Graph $G_{I I}$ ist $f_{k} (0) = 0 \Rightarrow 0 = (0 + k) \cdot e^{0} \Rightarrow k = k_{I I} = 0$ .
  Bei Graph $G_{I I I}$ ist $f_{k} (0) = - 4 \Rightarrow - 4 = (0 + k) \cdot e^{0} \Rightarrow k = k_{I I I} = - 4$ .
  Die zugehörigen Parameter sind $k_{I} = 2, k_{I I} = 0$ und $k_{I I I} = - 4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies jeweils $f_{k} (0)$ ab und setze in $f_{k} (x)$ ein $\Rightarrow k$ .
2. Begründen Sie, dass jede Funktion $f_{k}$ der Schar genau eine Nullstelle hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Begründe, dass jede Funktion $f_{k}$ der Schar genau eine Nullstelle hat
  Es ist $f_{k} (x) = 0 = (x^{3} + k) \cdot e^{x}$
  Wegen $e^{x} \neq 0$ für alle $x \in ℝ$ $\Rightarrow 0 = x^{3} + k \Rightarrow x^{3} = - k$
  Die Gleichung hat für alle $k \in ℝ$ genau eine Lösung: $x = - \sqrt[3]{k}$ für $k \geq 0$ bzw. $x = \sqrt[3]{- k}$ für $k < 0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $f_{k} (x) = 0 = (x^{3} + k) \cdot e^{x}$ .
  Löse die Gleichung nach $x$ auf.
  Mache eine Fallunterscheidung bzgl. $k$ .
3. Für die Ableitungsfunktion $f_{k}^{'}$ gilt:
  $f_{k}^{'} (x) = (x^{3} + 3 x^{2} + k) \cdot e^{x}, x \in ℝ; k \in ℝ .$
  Um die Abhängigkeit der Anzahl der Extremstellen der Funktion $f_{k}$ vom Parameter $k$ näher zu betrachten, wird die Funktion $h_{k}$ mit $h_{k} (x) = x^{3} + 3 x^{2} + k$ auf Nullstellen untersucht.
  Abbildung 5 zeigt den Graphen der Funktion $h_{0}$ (also $k = 0$ ).
  Abbildung 5
  (i) Geben Sie anhand von Abbildung 5 die Anzahl der Nullstellen der Funktion $h_{k}$ in Abhängigkeit vom Parameter $k$ an. (2 P)
  (Von einer Berechnung der Nullstellen im Taschenrechner ist abzusehen.)
  (ii) Begründen Sie die Richtigkeit der folgenden drei Aussagen:
  S1: Für jedes $k > 0$ hat die Funktion $f_{k}$ genau eine Extremstelle. (2 P)
  S2: Es gibt keine Funktion $f_{k}$ , die mehr als drei Extremstellen hat. (1 P)
  S3: Es gibt keine Funktion $f_{k}$ , die genau zwei Extremstellen hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  (i) Gib anhand von Abbildung 5 die Anzahl der Nullstellen der Funktion $h_{k}$ in Abhängigkeit vom Parameter $k$ an
  Es gibt genau zwei Nullstellen für $k = 0$ oder $k = - 4$ .
  Es gibt genau eine Nullstelle für $k > 0$ oder $k < - 4$ .
  Es gibt genau drei Nullstellen für $- 4 < k < 0$ .
  (ii) Begründe die Richtigkeit der folgenden drei Aussagen
  Aussage S1: Für $k > 0$ hat die Funktion $h_{k}$ und damit auch die Funktion $f_{k}^{'}$ genau eine Nullstelle mit Vorzeichenwechsel. $f_{k}$ hat daher genau eine Extremstelle.
  Aussage S2: Die Funktion $h_{k}$ kann als Polynomfunktion vom Grad 3 maximal drei Nullstellen haben. Wegen der notwendigen Bedingung $f_{k}^{'} (x) = 0$ für Extremstellen kann es nicht mehr als drei Extremstellen für die Funktion $f_{k}$ geben.
  Aussage S3: Die Funktion $h_{k}$ hat nur für $k = 0$ oder $k = 4$ zwei Nullstellen. Dabei handelt es sich um eine Nullstelle mit und eine Nullstelle ohne Vorzeichenwechsel. Deshalb gibt es in diesen Fällen nur eine Extremstelle und eine Sattelstelle für die Funktion $f_{k}$ .
  Anmerkung: Aus der Abbildung ist ersichtlich, dass im Falle von genau drei Nullstellen jeweils ein Vorzeichenwechsel vorliegt und dann drei Extremstellen existieren.
  Z. B. hat die Funktion $h_{- 1} (x) = (x^{3} + 3 x^{2} - 1) e^{x}$ drei Nullstellen mit Vorzeichenwechsel und $f_{- 1} (x) = (x^{3} - 1) \cdot e^{x}$ hat dann drei Extrema (2 $T P$ und 1 $H P$ ).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Für welche Werte von $k$ gibt es eine, zwei oder drei Nullstellen?
  (ii)
  Vergleiche die Aussage $S 1, S 2$ und $S 3$ mit der Anzahl der Nullstellen.