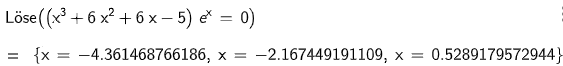B1 - lernen mit Serlo!

Aufgabe 1

Die Funktion $f$ ist gegeben durch die Gleichung

$f(x)=(x^3-5)e^x, x\in \mathbb{R}$ .

Der Graph von $f$ ist in Abbildung 1 dargestellt.

Berechnen Sie die Gleichung der Tangente an den Graphen von $f$ im Punkt $P(-1 \mid f(-1))$ , ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Berechne die Gleichung der Tangente an den Graphen von $f$ im Punkt $P(-1 \mid f(-1))$
Gegeben ist $f (x) = (x^{3} - 5) e^{x}$ .
Berechne $f^{'} (x)$ mit der Produktregel: $f'(x)=3x^2\cdot e^x+(x^3-5)\cdot e^x=(x^3+3x^2-5)\cdot e^x$
Für die Steigung der Tangente muss gelten: $m=f^{\prime}(-1)=-3 \cdot \mathrm{e}^{-1}$ .
Berechne $f(-1)=(-1-5)\cdot e^{-1}=-6\cdot e^{-1}$ .
Mit der Punktsteigungsform erhält man die Tangentengleichung:
$y=-3 \cdot \mathrm{e}^{-1} \cdot(x+1)-6 \cdot \mathrm{e}^{-1}$ oder $\left(y=-3 \cdot \mathrm{e}^{-1} \cdot x-9 \cdot \mathrm{e}^{-1}\right)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f^{'} (x)$ .
Für die Steigung der Tangente muss gelten: $m=f^{\prime}(-1)$ .
Berechne $f (- 1)$ .
Mit der Punktsteigungsform erhält man die Tangentengleichung.
Der Graph von $f$ besitzt genau eine Extremstelle und drei Wendestellen.
Berechnen Sie die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet
Berechne $f^{''} (x)$ und löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
$f'(x)=(x^3+3x^2-5)\cdot e^x$
$\Rightarrow\;f''(x)=(3x^2+6x)\cdot e^x+(x^3+3x^2-5)\cdot e^x=(x^3+6x^2+6x-5)\cdot e^x$
Löse die Gleichung $f^{''} (x) = 0$ :
Die Gleichung hat die Lösungen $x_{W 1}, x_{W 2}$ und $x_{W 3}$ mit $x_{W 1} \approx-4{,}361, x_{W 2} \approx-2{,}167$ und $x_{W 3} \approx 0{,}529$ .
Anmerkung: Da die Existenz von drei Wendestellen durch die Aufgabenstellung gesichert ist, ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
Die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet sind
$x_{W 1} \approx-4{,}361, x_{W 2} \approx-2{,}167$ und $x_{W 3} \approx 0{,}529$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f^{''} (x)$ und löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
Hinweis: Es ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
Für $z > 0$ ist $P_{z}(z \mid f(z))$ ein Punkt auf dem Graphen von $f$ . Er bildet zusammen mit dem Koordinatenursprung $O(0 \mid 0)$ und dem Punkt $Q_{z}(z \mid 0)$ ein Dreieck $O P_{z} Q_{z}$ .
Bestimmen Sie den Flächeninhalt des Dreiecks $\mathrm{OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Bestimme den Flächeninhalt des Dreiecks $\mathrm{OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird
Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $TP(1{,}1 \mid-11)$ .
Dann erhält man für den Flächeninhalt des Dreiecks:
$A_{\text {Dreieck }}=\dfrac{1}{2}\cdot g \cdot h \approx \frac{1}{2} \cdot 1{,}1 \cdot 11=6{,}05$ .
Der Flächeninhalt des Dreiecks $\mathrm{OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird, beträgt rund $6{,}05\;\mathrm{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $T P (x_{1} ∣ y_{1})$ .
Dann ist $A_{\text {Dreieck }} \approx \frac{1}{2} \cdot x_1 \cdot y_1$ $[\mathrm{FE}]$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 1

Berechne die Gleichung der Tangente an den Graphen von fff im Punkt P(−1∣f(−1))P(-1 \mid f(-1))P(−1∣f(−1))

Hast du eine Frage oder Feedback?

Berechne die Wendestellen der Funktion fff auf drei Nachkommastellen gerundet

Hast du eine Frage oder Feedback?

Bestimme den Flächeninhalt des Dreiecks OPzQz\mathrm{OP}_{z} Q_{z}OPz​Qz​, wenn für PzP_{z}Pz​ der Tiefpunkt des Graphen von fff gewählt wird

Hast du eine Frage oder Feedback?

Berechne die Gleichung der Tangente an den Graphen von $f$ im Punkt $P(-1 \mid f(-1))$

Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet

Bestimme den Flächeninhalt des Dreiecks $\mathrm{OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird