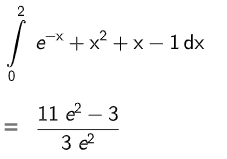Beschreibe, wie der Graph von $q^{\prime }$ aus dem Graphen von $q$ erzeugt werden kann

Gegeben: $q(x)=e^{-x}$

Weiterhin: Für die erste Ableitungsfunktion von $q$ gilt $q^{\prime }(x)=-q(x)$.

Der Graph von $q^{\prime }$ kann aus dem Graphen von $q$ durch eine Spiegelung an der $x$-Achse erzeugt werden.

Zeige, dass die Graphen von $p$ und $q$ in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben

Gegeben: $p(x)=-x^2-x+1$ und $q(x)=e^{-x}$

Die Graphen von $p$ und $q$ haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der $y$-Achse.

Für $x=0$ ist $p(0)=1$ und $q(0)=e^0=1$.

Der gemeinsame Punkt liegt auf der $y$-Achse und ist der Punkt $P(0|1)$.

Weiterhin gilt: $p^{\prime }(x)=-2x-1$ und $q^{\prime }(x)=-e^{-x}$:

Dann ist $p^{\prime }(0)=-1$ und $q^{\prime }(0)=-1$.

Die Graphen von $p$ und $q$ haben einen gemeinsamen Punkt $P(0|1)$ und sie haben in diesem Punkt die gleiche Steigung $-1$. Deshalb haben sie auch im Punkt $P$ eine gemeinsame Tangente.

Gib eine Gleichung dieser Tangente an

$t(x)=m\cdot x+b$ mit $m=-1$ und $b=1$ folgt dann:

$t(x)=-x+1$

Die Gleichung dieser Tangente lautet $t(x)=-x+1$.

Gib den Wert des Integrals $${\displaystyle {\int }_0^2(q(x)-p(x))\mathrm{d}x}$$ an und interpretiere diesen Wert geometrisch

$${\displaystyle {\int }_0^2(q(x)-p(x))\mathrm{d}x={\displaystyle {\int }_0^2(e^{-x}-(-x^2-x+1))\mathrm{d}x={\displaystyle {\int }_0^2(e^{-x}+x^2+x-1))\mathrm{d}x}}}$$

Der Term ${\displaystyle \frac{11\cdot e^2-3}{3\cdot e^2}}$ kann noch vereinfacht werden.

$$\Rightarrow {\displaystyle {\int }_0^2(q(x)-p(x))\mathrm{d}x={\displaystyle \frac{11}{3}}-e^{-2}\approx \mathrm{3,53}}$$

Die Fläche, die die Graphen von $p$ und $q$ sowie die Gerade mit der Gleichung $x=2$ einschließen, hat einen Inhalt von ca. $\mathrm{3,53}$ Flächeneinheiten.