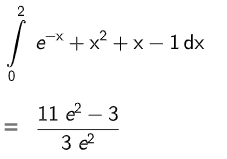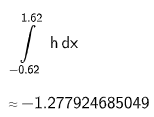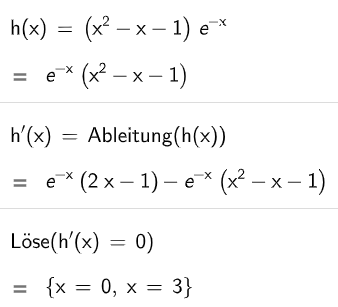B1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind die in $ℝ$ definierten Funktionen $p : x \mapsto - x^{2} - x + 1$ und $q : x \mapsto e^{- x}$ .
Die Graphen von $p$ und $q$ haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der $y$ -Achse. Für die erste Ableitungsfunktion von $q$ gilt $q^{'} (x) = - q (x)$ .
1. Beschreiben Sie, wie der Graph von $q^{'}$ aus dem Graphen von $q$ erzeugt werden kann. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen
  Beschreibe, wie der Graph von $q^{'}$ aus dem Graphen von $q$ erzeugt werden kann
  Gegeben: $q (x) = e^{- x}$
  Weiterhin: Für die erste Ableitungsfunktion von $q$ gilt $q^{'} (x) = - q (x)$ .
  Der Graph von $q^{'}$ kann aus dem Graphen von $q$ durch eine Spiegelung an der $x$ -Achse erzeugt werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Was bewirkt eine Spiegelung an der x-Achse?
2. Zeigen Sie, dass die Graphen von $p$ und $q$ in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und geben Sie eine Gleichung dieser Tangente an.
  (2 P + 1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Zeige, dass die Graphen von $p$ und $q$ in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben
  Gegeben: $p (x) = - x^{2} - x + 1$ und $q (x) = e^{- x}$
  Die Graphen von $p$ und $q$ haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der $y$ -Achse.
  Für $x = 0$ ist $p (0) = 1$ und $q (0) = e^{0} = 1$ .
  Der gemeinsame Punkt liegt auf der $y$ -Achse und ist der Punkt $P (0 | 1)$ .
  Weiterhin gilt: $p^{'} (x) = - 2 x - 1$ und $q^{'} (x) = - e^{- x}$ :
  Dann ist $p^{'} (0) = - 1$ und $q^{'} (0) = - 1$ .
  Die Graphen von $p$ und $q$ haben einen gemeinsamen Punkt $P (0 | 1)$ und sie haben in diesem Punkt die gleiche Steigung $- 1$ . Deshalb haben sie auch im Punkt $P$ eine gemeinsame Tangente.
  Gib eine Gleichung dieser Tangente an
  $t (x) = m \cdot x + b$ mit $m = - 1$ und $b = 1$ folgt dann:
  $t (x) = - x + 1$
  Die Gleichung dieser Tangente lautet $t (x) = - x + 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Die Graphen von $p$ und $q$ haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der $y$ -Achse. Setze $x = 0$ in die Funktionsgleichungen ein.
  Berechne $p^{'} (0)$ und $q^{'} (0)$ .
  Teil 2
  Setze die bekannten Werte in $t (x) = m \cdot x + b$ ein.
3. Geben Sie den Wert des Integrals $\int_{0}^{2} (q (x) - p (x)) d x$ an und interpretieren Sie diesen Wert geometrisch. (1 P + 2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  Gib den Wert des Integrals $\int_{0}^{2} (q (x) - p (x)) d x$ an und interpretiere diesen Wert geometrisch
  $\int_{0}^{2} (q (x) - p (x)) d x = \int_{0}^{2} (e^{- x} - (- x^{2} - x + 1)) d x = \int_{0}^{2} (e^{- x} + x^{2} + x - 1)) d x$
  Der Term $\frac{11 \cdot e^{2} - 3}{3 \cdot e^{2}}$ kann noch vereinfacht werden.
  $\Rightarrow \int_{0}^{2} (q (x) - p (x)) d x = \frac{11}{3} - e^{- 2} \approx 3,53$
  Die Fläche, die die Graphen von $p$ und $q$ sowie die Gerade mit der Gleichung $x = 2$ einschließen, hat einen Inhalt von ca. $3,53$ Flächeneinheiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze in $\int_{0}^{2} (q (x) - p (x)) d x$ die beiden gegebenen Funktionen ein und berechne das Integral.
  Der Wert des Integrals ist die von den beiden Graphen eingeschlossene Fläche zwischen $x = 0$ und $x = 2$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Gegeben ist die in $ℝ$ definierte Funktion $h : x \mapsto (x^{2} - x - 1) \cdot e^{- x}$ .
1. Bestimmen Sie die Größe der Fläche, die der Graph von $h$ und die $x$ -Achse einschließen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme die Größe der Fläche, die der Graph von $h$ und die $x$ -Achse einschließen
  Gegeben: $h (x) = (x^{2} - x - 1) \cdot e^{- x}$
  Berechne die Nullstellen $h (x) = 0$ :
  $0 = (x^{2} - x - 1) \cdot e^{- x}$
  Verwende Satz vom Nullprodukt:
  $e^{- x} \neq 0$ für alle $x \Rightarrow x^{2} - x - 1 = 0$
  Der TR liefert $x \approx - 0,62 \lor x \approx 1,62$ .
  Berechne nun das Integral $A = | \int_{- 0,62}^{1,62} h (x) d x | \approx 1,28$
  Die Größe der Fläche, die der Graph von $h$ und die $x$ -Achse einschließen, beträgt rund $1,28 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Nullstellen $h (x) = 0$ $\Rightarrow x_{1}$ und $x_{2}$ .
  Dann berechnet man den Flächeninhalt mit $A = | \int_{x_{1}}^{x_{2}} h (x) d x |$ .
2. (i) Zeigen Sie: $h^{'} (x) = (- x^{2} + 3 x) \cdot e^{- x}$ . (2 P)
  (ii) Berechnen Sie die Koordinaten der beiden Extrempunkte des Graphen von $h$ sowie den Abstand der Extrempunkte. (2 P + 2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  (i) Zeige: $h^{'} (x) = (- x^{2} + 3 x) \cdot e^{- x}$
  Wende die Produkt- und Kettenregel an. $h^{'} (x) = (2 x - 1) \cdot e^{- x} - (x^{2} - x - 1) \cdot e^{- x} = (- x^{2} + 3 x) \cdot e^{- x}$ .
  (ii) Berechne die Koordinaten der beiden Extrempunkte des Graphen von h sowie den Abstand der Extrempunkte
  Notwendige Bedingung für Extremstellen: $h^{'} (x) = 0$ .
  Die Nullstellen sind also $x = 0 \lor x = 3$ .
  Laut Aufgabenstellung hat der Graph von $h$ nur zwei Extrempunkte.
  Da $h^{'}$ nur zwei Nullstellen besitzt, muss es sich um die Extremstellen handeln.
  Gesucht ist also der Abstand $d$ der Punkte $T (0 | h (0)) = T (0 | - 1)$ und $H (3 | h (3)) = H (3 | 5 e^{- 3})$ .
  Es gilt: $d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$
  $\Rightarrow d = \sqrt{(3 - 0)^{2} + (5 e^{- 3} - (- 1))^{2}} \approx 3,25$
  Der Abstand der Extrempunkte beträgt rund $3,25 LE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Wende die Produkt- und Kettenregel an.
  (ii)
  Berechne für die Extrema $h^{'} (x) = 0$ . $\Rightarrow x_{1}$ und $x_{2}$
  Berechne die Koordinaten der beiden Extrema $T P (x_{1} | h (x_{1})$ und $H P (x_{2} | h (x_{2})$ .
  Der Abstand der Extrempunkte berechnet sich dann mit: $d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$ .
3. Die beiden Extrempunkte $T$ und $H$ des Graphen von $h$ bilden zusammen mit den Punkten $P$ und $Q$ ein Rechteck $T P H Q$ , dessen Seiten parallel zu den Koordinatenachsen verlaufen. Dieses Rechteck wird durch den Graphen der Funktion $h$ in zwei Teilstücke zerlegt
  (siehe Abbildung 1).
  Ermitteln Sie, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt. (2 P + 2 P + 2 P)
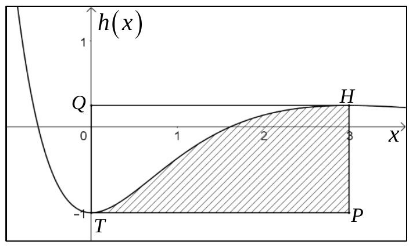
  Abbildung 1
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Ermittele, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt
  Gegeben: $T (0 | - 1)$ und $H (3 | 5 e^{- 3})$ .
  Der Flächeninhalt des Rechtecks $T P H Q$ berechnet sich durch:
  $A_{□} = Δ x \cdot Δ y = 3 \cdot (5 e^{- 3} + 1) \approx 3,75$ .
  Der Flächeninhalt des Rechtecks beträgt rund $3,75 FE$ .
  Schraffiert ist die Fläche zwischen dem Graphen von $h$ und der Geraden mit der Gleichung $y = - 1$ über dem Intervall $[0; 3]$ .
  Ihr Inhalt beträgt $A_{schraffiert} = \int_{0}^{3} (h (x) - (- 1)) d x \approx 2,40$ .
  Der Inhalt der schraffierten Fläche $A_{schraffiert}$ beträgt rund $2,40 FE$ .
  Damit ergibt sich ein Anteil von $\frac{A_{schraffiert}}{A_{□}} = \frac{2,40}{3 \cdot (5 e^{- 3} + 1)} \approx 0,641$ , also von ca. $64,1 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Koordinaten der beiden Extrema und berechne den Flächeninhalt $A_{□}$ des Rechtecks.
  Berechne den Inhalt der schraffierten Fläche mit: $A_{schraffiert} = \int_{0}^{3} (h (x) - (- 1)) d x$
  Bilde das Verhältnis $\frac{A_{schraffiert}}{A_{□}}$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in $ℝ$ definierte Funktion $w : x \mapsto 4 \cdot (x^{2} - x - 1) \cdot e^{- x} + 4$ beschreibt für $x \geq 0$ die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Sekunden und $w (x)$ die momentane Durchflussrate in Kubikmetern pro Sekunde.
Abbildung 2 zeigt den Graphen von $w$ .
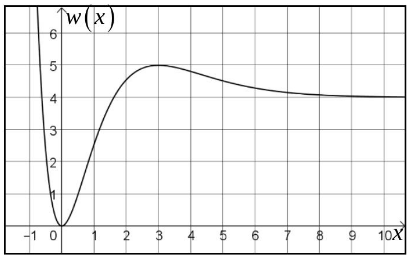
Abbildung 2
1. Für $x \to \infty$ gilt $w (x) \to c$ .
  Geben Sie den Wert $c$ sowie die Bedeutung dieses Wertes im Sachzusammenhang an.
  (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert bestimmen
  Gib den Wert $c$ sowie die Bedeutung dieses Wertes im Sachzusammenhang an
  Gegeben ist $w (x) = 4 \cdot (x^{2} - x - 1) \cdot e^{- x} + 4$
  Es gilt: $\lim_{x \to \infty} x^{n} \cdot e^{- x} = 0$ . Daher ist $\lim_{x \to \infty} w (x) = 4$ .
  Demnach ist $c = 4$ , d. h., die momentane Durchflussrate nähert sich langfristig einem Wert von $4 \frac{m^{3}}{s}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $w (x)$ beschreibt für $x \geq 0$ die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle.
  Es gilt: $\lim_{x \to \infty} x^{n} \cdot e^{- x} = 0$ . Daher ist $\lim_{x \to \infty} w (x) = 4$ .
  Welche Schlussfolgerung kann man ziehen?
2. Ohne Nachweis können Sie im Weiteren $w^{'} (x) = (12 x - 4 x^{2}) \cdot e^{- x}$ verwenden.
  Es gibt zwei Stellen, an denen die momentane Änderungsrate der Funktion $w$ mit der mittleren Änderungsrate der Funktion $w$ über dem Intervall $[0; 10]$ übereinstimmt. Ermitteln Sie eine dieser Stellen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Die mittlere Änderungsrate – Einführung der Ableitung
  Ermittele eine dieser Stellen
  Die momentane Änderungsrate der Funktion $w$ ist $w^{'} (x)$ .
  Die mittlere Änderungsrate der Funktion $w$ über dem Intervall $[0; 10]$ wird berechnet mit $\frac{w (10) - w (0)}{10 - 0}$ .
  Damit erhält man folgende Gleichung:
  $w^{'} (x) = \frac{w (10) - w (0)}{10}$
  Der GTR liefert für die Gleichung $w^{'} (x) = \frac{w (10) - w (0)}{10}$ eine Lösung $x_{3}$ mit
  $x_{3} \approx 0,04$ . (Für die zweite Lösung $x_{4}$ gilt: $x_{4} \approx 2,51$ .)
  An der Stelle $x_{3} \approx 0,04$ stimmt die momentane Änderungsrate der Funktion $w$ mit der mittleren Änderungsrate der Funktion $w$ über dem Intervall $[0; 10]$ überein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die momentane Änderungsrate der Funktion $w$ ist $w^{'} (x)$ .
  Die mittlere Änderungsrate der Funktion $w$ über dem Intervall $[0; 10]$ wird berechnet mit $\frac{w (10) - w (0)}{10 - 0}$ .
  Damit erhält man folgende Gleichung, die gelöst werden muss: $w^{'} (x) = \frac{w (10) - w (0)}{10}$
3. Bestimmen Sie denjenigen Zeitpunkt in den ersten zehn Sekunden nach Beobachtungsbeginn, zu dem die momentane Durchflussrate am stärksten abnimmt. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Bestimmen Sie denjenigen Zeitpunkt in den ersten zehn Sekunden nach Beobachtungsbeginn, zu dem die momentane Durchflussrate am stärksten abnimmt
  Betrachte den Graphen der Funktion $w$ . Die stärkste Abnahme liegt an derjenigen Wendestelle $x_{w}$ vor, für die $x_{w} > 3$ gilt. Die Analyse des Graphen von $w^{'}$ ergibt als zugehörigen Tiefpunkt $T P (4,3 | - 0,303)$ .
  Damit liegt die stärkste Abnahme der momentanen Durchflussrate in den ersten zehn Sekunden nach Beobachtungsbeginn ungefähr $4,3$ Sekunden nach Beobachtungsbeginn vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte den Graphen der Funktion $w$ . Die stärkste Abnahme liegt an derjenigen Wendestelle $x_{w}$ vor, für die $x_{w} > 3$ gilt.
  Analysiere den Graphen von $w^{'}$ , um den zugehörigen Tiefpunkt zu finden.
4. (i) Bestimmen Sie die Wassermenge, die in den ersten zwei Sekunden seit Beobachtungsbeginn an der Messstelle vorbeifließt. (2 P)
  (ii) Die Gleichung $\int_{t}^{t + 3} w (x) d x = 13$ hat für $t \geq 0$ die Lösungen $t_{1}$ und $t_{2}$ mit $t_{1} \approx 0,8$ und $t_{2} \approx 4,4$ .
  Interpretieren Sie die Bedeutung dieser beiden Lösungen im Sachzusammenhang. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  (i) Bestimme die Wassermenge, die in den ersten zwei Sekunden seit Beobachtungsbeginn an der Messstelle vorbeifließt
  Berechne:
  $\int_{0}^{2} w (x) d x \approx 4,75$
  In den ersten zwei Sekunden ab Messbeginn fließen ca. $4,75 m^{3}$ Wasser an der Messstelle vorbei.
  (ii) Interpretieren Sie die Bedeutung dieser beiden Lösungen im Sachzusammenhang
  Die erhaltenen Zeitpunkte markieren jeweils den Beginn eines drei Sekunden umfassenden Zeitraums, über den hinweg $13 m^{3}$ Wasser an der Messstelle vorbeigeflossen sind.
  D. h., von etwa $0,8 s$ bis $3,8 s$ nach Beobachtungsbeginn sowie von etwa $4,4 s$ bis $7,4 s$ nach Beobachtungsbeginn beträgt der Wasserdurchfluss jeweils $13 m^{3}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Berechne $\int_{0}^{2} w (x) d x$ .
  (ii)
  Die erhaltenen Zeitpunkte markieren jeweils den Beginn eines drei Sekunden umfassenden Zeitraums, über den hinweg $13 m^{3}$ Wasser an der Messstelle vorbeigeflossen sind.
  Um welche beiden Zeiträume handelt es sich dann?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B1

Aufgabe 1

Beschreibe, wie der Graph von q′ aus dem Graphen von q erzeugt werden kann

Hast du eine Frage oder Feedback?

Zeige, dass die Graphen von p und q in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben

Gib eine Gleichung dieser Tangente an

Hast du eine Frage oder Feedback?

Gib den Wert des Integrals ∫02(q(x)−p(x))dx an und interpretiere diesen Wert geometrisch

Hast du eine Frage oder Feedback?

Aufgabe 2

Bestimme die Größe der Fläche, die der Graph von h und die x-Achse einschließen

Hast du eine Frage oder Feedback?

(i) Zeige: h′(x)=(−x2+3x)⋅e−x

(ii) Berechne die Koordinaten der beiden Extrempunkte des Graphen von h sowie den Abstand der Extrempunkte

Hast du eine Frage oder Feedback?

Ermittele, welchen Anteil an der Fläche des Rechtecks die Fläche des schraffierten Teilstücks einnimmt

Hast du eine Frage oder Feedback?

Aufgabe 3

Gib den Wert c sowie die Bedeutung dieses Wertes im Sachzusammenhang an

Hast du eine Frage oder Feedback?

Ermittele eine dieser Stellen

Hast du eine Frage oder Feedback?

Bestimmen Sie denjenigen Zeitpunkt in den ersten zehn Sekunden nach Beobachtungsbeginn, zu dem die momentane Durchflussrate am stärksten abnimmt

Hast du eine Frage oder Feedback?

(i) Bestimme die Wassermenge, die in den ersten zwei Sekunden seit Beobachtungsbeginn an der Messstelle vorbeifließt

(ii) Interpretieren Sie die Bedeutung dieser beiden Lösungen im Sachzusammenhang

Hast du eine Frage oder Feedback?

Beschreibe, wie der Graph von $q^{'}$ aus dem Graphen von $q$ erzeugt werden kann

Zeige, dass die Graphen von $p$ und $q$ in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben

Gib den Wert des Integrals $\int_{0}^{2} (q (x) - p (x)) d x$ an und interpretiere diesen Wert geometrisch

Bestimme die Größe der Fläche, die der Graph von $h$ und die $x$ -Achse einschließen

(i) Zeige: $h^{'} (x) = (- x^{2} + 3 x) \cdot e^{- x}$

Gib den Wert $c$ sowie die Bedeutung dieses Wertes im Sachzusammenhang an