Aufgabe 3
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in definierte Funktion beschreibt für die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und die momentane Durchflussrate in Kubikmetern pro Sekunde.
Abbildung 2 zeigt den Graphen von .
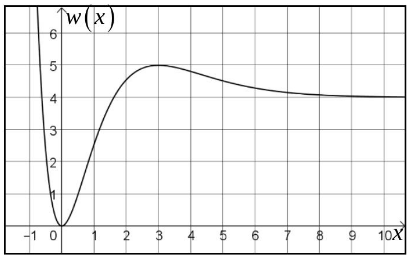
Abbildung 2
Für gilt .
Geben Sie den Wert sowie die Bedeutung dieses Wertes im Sachzusammenhang an.
(2 P)
Ohne Nachweis können Sie im Weiteren verwenden.
Es gibt zwei Stellen, an denen die momentane Änderungsrate der Funktion mit der mittleren Änderungsrate der Funktion über dem Intervall übereinstimmt. Ermitteln Sie eine dieser Stellen. (3 P)
Bestimmen Sie denjenigen Zeitpunkt in den ersten zehn Sekunden nach Beobachtungsbeginn, zu dem die momentane Durchflussrate am stärksten abnimmt. (3 P)
(i) Bestimmen Sie die Wassermenge, die in den ersten zwei Sekunden seit Beobachtungsbeginn an der Messstelle vorbeifließt. (2 P)
(ii) Die Gleichung hat für die Lösungen und mit und .
Interpretieren Sie die Bedeutung dieser beiden Lösungen im Sachzusammenhang. (2 P)
