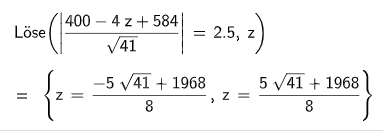Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
In einem kartesischen Koordinatensystem sind die Punkte , und sowie der Punkt gegeben.
Bekannt sind außerdem und .
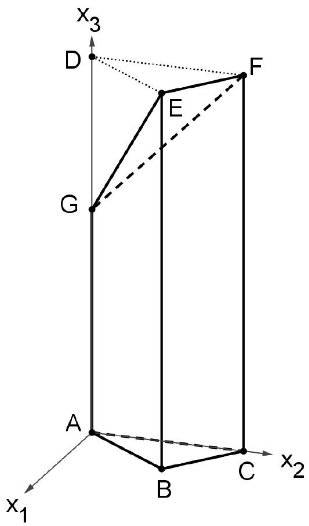
Abbildung
Durch , ist eine Schar von parallelen Ebenen gegeben. Die Dachfläche liegt in der Ebene . Es gibt einen Wert von , sodass gilt.
Bestimmen Sie so, dass gilt.
Zur Kontrolle: . (1 P)
Berechnen Sie den Winkel zwischen und der Ebene , in der die Wandfläche liegt. (2 P + 2 P)
Oberhalb der Dachfläche soll in einer Ebene, die parallel zur Dachfläche verläuft, eine Fläche mit Solarkollektoren entstehen (siehe Abbildung 2).
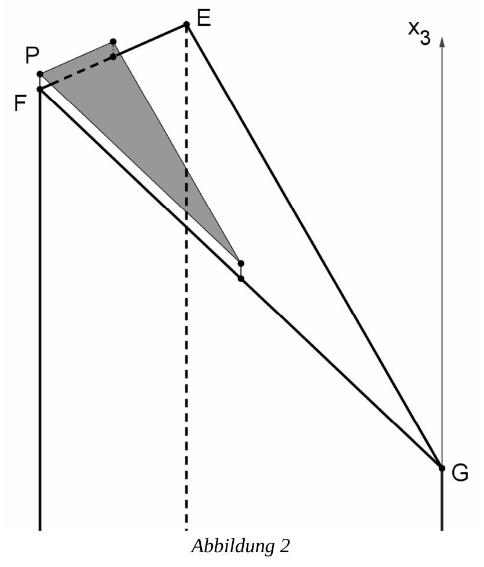
Diese Ebene hat einen Abstand von zur Dachfläche .
Bestimmen Sie rechnerisch die -Koordinate des Befestigungspunktes .
(2 P)