B1 - lernen mit Serlo!

Aufgabe 3

Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.

Gegeben ist die Funktion $f$ mit der Gleichung $f(x)=9 \cdot(x-3) \cdot \mathrm{e}^{-1{,}5 \cdot(x-3)}, x \in \mathbb{R}$ .

Für $k \in \mathbb{R}$ und $k > 0$ ist die Funktionenschar $g_{k}$ gegeben durch die Gleichung

$g_{k}(x)=4 \cdot k^{2} \cdot(x-3) \cdot \mathrm{e}^{-k \cdot(x-3)}, x \in \mathbb{R}$ .

Es gilt $g_{1{,}5}=f$ .

Begründen Sie, dass alle Graphen von Funktionen der Schar $g_{k}$ nur einen Schnittpunkt mit der $x$ -Achse haben. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Begründe, dass alle Graphen von Funktionen der Schar $g_{k}$ nur einen Schnittpunkt mit der $x$ -Achse haben
Mit $\mathrm{e}^{-k \cdot(x-3)}>0$ für alle $x \in \mathbb{R}$ und $k^{2}>0$ gilt:
$g_{k}(x)=4 \cdot k^{2} \cdot(x-3) \cdot \mathrm{e}^{-k \cdot(x-3)}=0 \Leftrightarrow(x-3)=0 \Leftrightarrow x=3$ .
Somit gibt es nur einen Schnittpunkt mit der $x$ -Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $g_{k}(x)=0$ .
Ohne Nachweis darf verwendet werden: $g_{k}^{\prime \prime}\left(3+\frac{1}{k}\right)=-4 \cdot k^{3} \cdot \mathrm{e}^{-1}$ .
Bestimmen Sie rechnerisch die Extremstelle und die Art des Extrempunktes des Graphen von $g_{k}$ in Abhängigkeit von $k$ . $[$ Zur Kontrolle: Die Extremstelle ist $x=3+\frac{1}{k}$ . $]$ (3 P + 4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Bestimme rechnerisch die Extremstelle und die Art des Extrempunktes des Graphen von $g_{k}$ in Abhängigkeit von $k$
Gegeben ist $g_{k}(x)=4 \cdot k^{2} \cdot(x-3) \cdot \mathrm{e}^{-k \cdot(x-3)}$ .
Berechne $g_{k}'(x)=4 \cdot k^{2} \cdot\left(1 \cdot \mathrm{e}^{-k \cdot(x-3)}+(x-3)\cdot(-k)\cdot\mathrm{e}^{-k \cdot(x-3)}\right)$ .
$g_{k}'(x)=4 \cdot k^{3} \cdot\left(-x+3+\frac{1}{k}\right)\cdot\mathrm{e}^{-k \cdot(x-3)}$
Aus der notwendigen Bedingung $g_{k}{ }^{\prime}(x)=0$ folgt:
$-x+3+\frac{1}{k}=0\;\Rightarrow\;x=3+\frac{1}{k}$
Überprüfe die Art des Extremums mit der 2. Ableitung:
$g_{k}''(3+\frac{1}{k})=4 \cdot k^{4} \cdot\left(3+\frac{1}{k}-3-\frac{2}{k}\right)\cdot\mathrm{e}^{-k \cdot(3+\frac{1}{k}-3)}$
$g_{k}''(3+\frac{1}{k})=-4k^3e^{-1}<0$ für alle $k > 0$ .
Der Graph der Funktion $g_{k}$ hat an der Stelle $x=3+\frac{1}{k}$ einen Hochpunkt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $g_{k}{ }^{\prime}(x)$ .
Aus der notwendigen Bedingung $g_{k}{ }^{\prime}(x)=0$ folgt $x_{1}$ .
Überprüfe die Art des Extremums mit der 2. Ableitung.
Die Funktion $G_{k}$ mit $G_{k}(x)=-4 \cdot k \cdot\left(x-3+\frac{1}{k}\right) \cdot \mathrm{e}^{-k \cdot(x-3)}$ ist eine Stammfunktion der Funktion $g_{k}$ .
Für $x \geq 3$ liegt zwischen der $x$ -Achse und dem Graphen der Funktion $g_{k}$ die nach rechts offene Fläche $A$ .
Prüfen Sie rechnerisch, ob der Inhalt der Fläche $A$ vom Parameter $k$ abhängt. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Prüfe rechnerisch, ob der Inhalt der Fläche $A$ vom Parameter $k$ abhängt
Berechne das Integral $\displaystyle\lim _{w \rightarrow \infty}\int_3^w g_k(x)\;\mathrm{d} x$ .
Gegeben: Die Funktion $G_{k}$ mit $G_{k}(x)=-4 \cdot k \cdot\left(x-3+\frac{1}{k}\right) \cdot \mathrm{e}^{-k \cdot(x-3)}$ ist eine Stammfunktion der Funktion $g_{k}$ .
Dann ist $\displaystyle\int_{3}^{w} g_{k}(x) \mathrm{d} x=\left[-4 \cdot k \cdot\left(x-3+\frac{1}{k}\right) \cdot \mathrm{e}^{-k \cdot(x-3)}\right]_{3}^{w}$
Die Grenzen eingesetzt, erhält man:
$\displaystyle\int_{3}^{w} g_{k}(x) \mathrm{d} x=-4 \cdot k \cdot\left(w-3+\frac{1}{k}\right) \cdot \mathrm{e}^{-k \cdot(w-3)}-(-4)$
$=-4 \cdot k \cdot\left(w-3+\frac{1}{k}\right) \cdot \mathrm{e}^{-k \cdot(w-3)}+4$
Der erste Summand wird von $\mathrm{e}^{-k \cdot(w-3)}$ dominiert.
Mit $k > 0$ gilt: $\displaystyle\lim _{w \rightarrow \infty}\left(\mathrm{e}^{-k \cdot(w-3)}\right)=0$
Es folgt: $\displaystyle\lim _{w \rightarrow \infty}\left(\int_{3}^{w} g_{k}(x) \;\mathrm{d} x\right)=4$ .
Der Flächeninhalt der Fläche $A$ beträgt somit, unabhängig vom Parameter $k, 4$ Flächeneinheiten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne das Integral $\displaystyle\lim _{w \rightarrow \infty}\int_3^w g_k(x)\;\mathrm{d} x$ .
Berechne zunächst $\displaystyle\int_3^w g_k(x)\;\mathrm{d} x=A(w)$
Berechne dann $\displaystyle\lim _{w \rightarrow \infty}A(w)$ .
Der Graph der Funktion $g_{k}$ hat den Hochpunkt $H_{k}$ mit $H_{k}\left(\left.3+\frac{1}{k} \right\rvert\, 4 \cdot k \cdot \mathrm{e}^{-1}\right)$ .
Die Graphen der Funktionen $g_{1{,}5}$ und $g_{2{,}6}$ schneiden sich nur im Punkt $N(3 \mid 0)$ und in einem weiteren Punkt $S$ .
(i) Geben Sie die Koordinaten des Hochpunktes des Graphen von $g_{2{,}6}$ an und bestimmen Sie die Koordinaten des Schnittpunktes $S$ der Graphen von $g_{1{,}5}$ und $g_{2{,}6}$ .
(2 P)
(ii) Skizzieren Sie mithilfe dieser Punkte den Graphen der Funktion $g_{2{,}6}$ in Abbildung 3. (2 P)
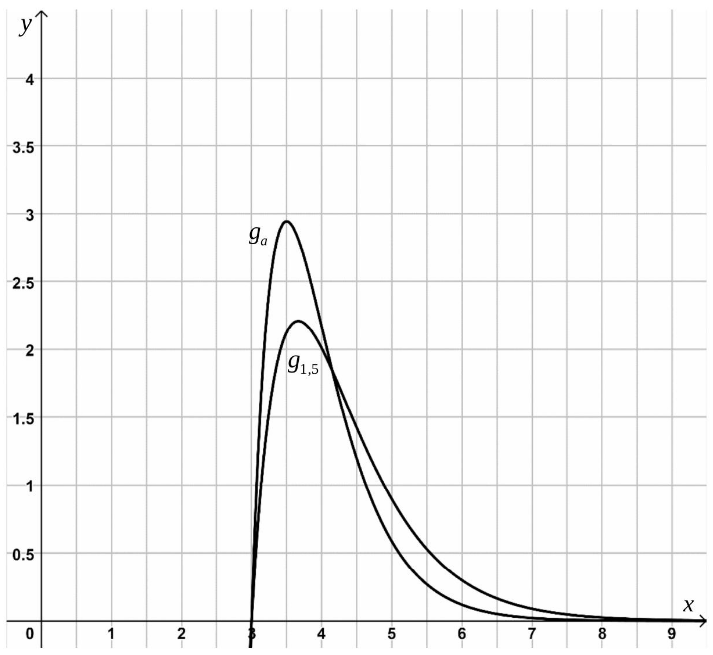
Abbildung 3
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
(i) Gib die Koordinaten des Hochpunktes des Graphen von $g_{2{,}6}$ an
Gegeben sind $g_{1{,}5}(x)=f(x)=9 \cdot(x-3) \cdot \mathrm{e}^{-1{,}5 \cdot(x-3)}$ und
$g_{2{,}6}(x)=4 \cdot 2{,}6^{2} \cdot(x-3) \cdot \mathrm{e}^{-k \cdot(x-3)}=27{,}04\cdot (x-3) \cdot \mathrm{e}^{-k \cdot(x-3)}$
Weiterhin: Der Graph der Funktion $g_{k}$ hat den Hochpunkt $H_{k}$ mit $H_{k}\left(\left.3+\frac{1}{k} \right\rvert\, 4 \cdot k \cdot \mathrm{e}^{-1}\right)$ .
Für den Hochpunkt des Graphen von $g_{2{,}6}$ erhält man: $H_{2{,}6}\left(\left.3+\frac{1}{2{,}6} \right\rvert\, 4 \cdot 2{,}6 \cdot \mathrm{e}^{-1}\right)\approx H_{2{,}6}(3{,}38\mid 3{,}83)$
Bestimme die Koordinaten des Schnittpunktes $S$ der Graphen von $g_{1{,}5}$ und $g_{2{,}6}$
Die grafische Analyse ergibt den ungefähren Schnittpunkt $S(4 \mid 2)$ .
(ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion $g_{2{,}6}$ in Abbildung 3
Es sind $HP(3{,}38\mid 3{,}83)$ und $S(4 \mid 2)$ gegeben.
Zeichne die Punkte in die Abbildung ein und verbinde sie mit einem passenden Graphen.
Abbildung 3
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
(i)
Teil 1
Setze $k = 2,6$ in die gegebenen Koordinaten des Hochpunktes ein.
Teil 2
Die grafische Analyse ergibt den ungefähren Schnittpunkt $S$ .
(ii)
Zeichne die Punkte $H P$ und $S$ in die Abbildung ein und verbinde sie mit einem passenden Graphen.
Für ein $a > 0$ ist der Graph der Funktion $g_{a}$ in Abbildung 3 dargestellt.
Begründen Sie anhand des Hochpunktes ohne weitere Berechnung, ob der Wert von $a$ größer oder kleiner ist als $1,5$ . (2 P)
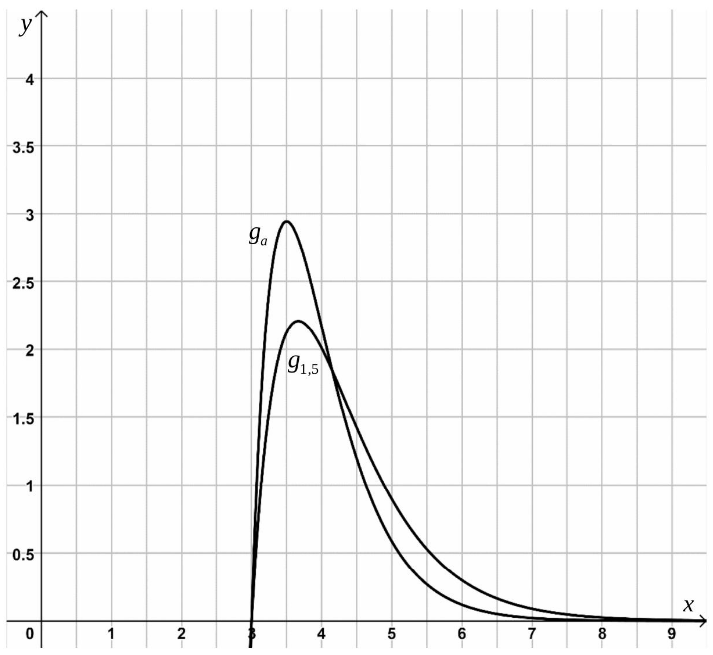
Abbildung 3
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Begründe anhand des Hochpunktes ohne weitere Berechnung, ob der Wert von $a$ größer oder kleiner ist als 1,5
Die $y$ -Koordinate des Hochpunktes des Graphen von $g_{a}$ ist größer als die $y$ -Koordinate des Hochpunktes des Graphen von $g_{1{,}5}$ . Da die $y$ -Koordinate des Hochpunktes linear mit $k$ wächst, muss der Parameter $a$ größer sein als $1,5$ . (Alternativ kann anhand der $x$ -Koordinate argumentiert werden.)
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die $y$ -Koordinate des Hochpunktes des Graphen von $g_{a}$ ist größer als die $y$ -Koordinate des Hochpunktes des Graphen von $g_{1{,}5}$ .
Die $y$ -Koordinate des Hochpunktes wächst linear mit $k$ .
Was bedeutet das für den Wert von $k$ ?

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 3

Begründe, dass alle Graphen von Funktionen der Schar gkg_{k}gk​ nur einen Schnittpunkt mit der xxx-Achse haben

Hast du eine Frage oder Feedback?

Bestimme rechnerisch die Extremstelle und die Art des Extrempunktes des Graphen von gkg_{k}gk​ in Abhängigkeit von kkk

Hast du eine Frage oder Feedback?

Prüfe rechnerisch, ob der Inhalt der Fläche AAA vom Parameter kkk abhängt

Hast du eine Frage oder Feedback?

(i) Gib die Koordinaten des Hochpunktes des Graphen von g2,6g_{2{,}6}g2,6​ an

Bestimme die Koordinaten des Schnittpunktes SSS der Graphen von g1,5g_{1{,}5}g1,5​ und g2,6g_{2{,}6}g2,6​

(ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion g2,6g_{2{,}6}g2,6​ in Abbildung 3

Hast du eine Frage oder Feedback?

Begründe anhand des Hochpunktes ohne weitere Berechnung, ob der Wert von aaa größer oder kleiner ist als 1,5

Hast du eine Frage oder Feedback?

Begründe, dass alle Graphen von Funktionen der Schar $g_{k}$ nur einen Schnittpunkt mit der $x$ -Achse haben

Bestimme rechnerisch die Extremstelle und die Art des Extrempunktes des Graphen von $g_{k}$ in Abhängigkeit von $k$

Prüfe rechnerisch, ob der Inhalt der Fläche $A$ vom Parameter $k$ abhängt

(i) Gib die Koordinaten des Hochpunktes des Graphen von $g_{2{,}6}$ an

Bestimme die Koordinaten des Schnittpunktes $S$ der Graphen von $g_{1{,}5}$ und $g_{2{,}6}$

(ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion $g_{2{,}6}$ in Abbildung 3

Begründe anhand des Hochpunktes ohne weitere Berechnung, ob der Wert von $a$ größer oder kleiner ist als 1,5