Das Schaubild zeigt Ausschnitte der Parabel $p_{1}p\_1$ und der Geraden $gg$.

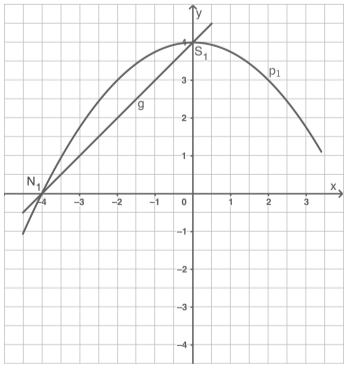
• Bestimme die Funktionsgleichungen von $p_{1}p\_1$ und $gg$ . Entnimm dazu geeignete Werte aus dem Schaubild.

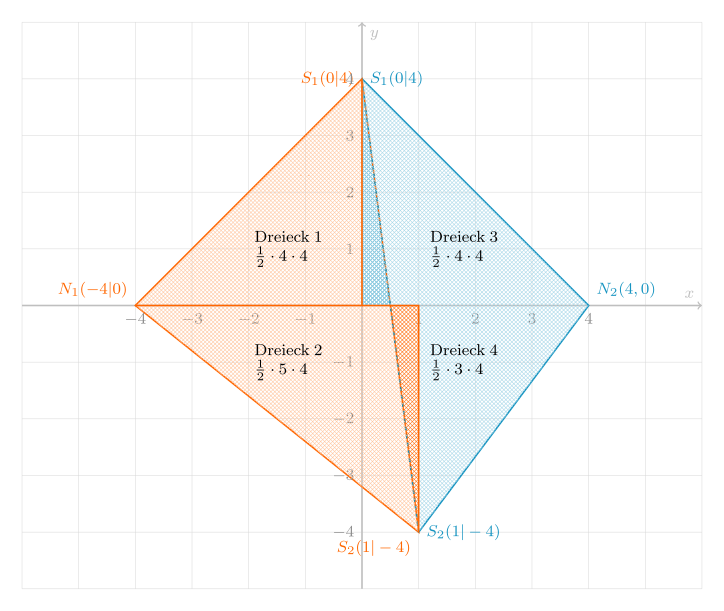
Die Parabel $p_{1}p\_1$ schneidet die $xx$-Achse in den Punkten $N_{1}N\_1$ und $N_{2}N\_2$.

• Gib die Koordinaten von $N_{2}N\_2$ an.

Die Parabel $p_{2}p\_2$ hat die Funktionsgleichung $y=x^2-2x-3y=x^2-2x-3$ .

• Berechne die Koordinaten des Scheitelpunktes $S_{2}S\_2$ von $p_{2}p\_2$.

$S_{2}S\_2$ bildet mit $S_{1}S\_1$ und $N_{1}N\_1$ das Dreieck $S_2{S}_1{N}_{1}S\_2S\_1N\_1$. Ebenso bildet $S_{2}S\_2$ mit $N_{2}N\_2$ und $S_{1}S\_1$ das Dreieck $S_2{N}_2{S}_{1}S\_2N\_2S\_1$.

• Um wie viele Flächeneinheiten (FE) unterscheiden sich die Flächeninhalte dieser beiden Dreiecke?

[ 5 P ]

Auf einem regelmäßigen achtseitigen Prisma liegt der Streckenzug $PQRSPQRS$ mit der Länge von $\mathrm{38,0}\text{ cm}\mathrm{.}38\{,\}0\backslash cm.$

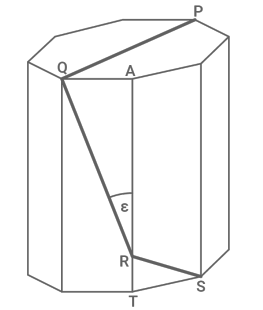
Es gilt:

$\overline{AR}=\mathrm{14,2}\text{ cm}\backslash overline\{AR\}=14\{,\}2\backslash cm$

$ϵ=\mathrm{23,0}\mathrm{°}\backslash epsilon=23\{,\}0°$

Berechne die Höhe des achtseitigen Prismas.

[ 5 P ]