Die Abbildung zeigt eine quadratische Pyramide.

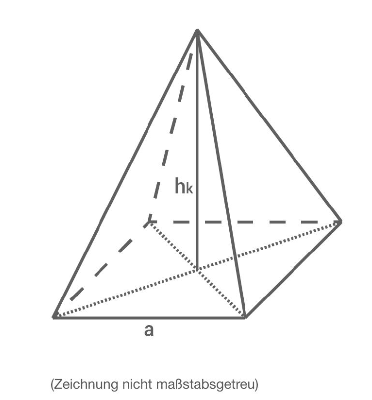
Es gilt:

$V=\mathrm{70,58}{\mathrm{c}\mathrm{m}}^3$ $h_k=7\mathrm{c}\mathrm{m}$

• Zeige rechnerisch, dass die Grundkante der Pyramide $\mathrm{5,5}\text{ cm}$ lang ist.

Aus einem DIN A4 - Blatt mit den Maßen $210\text{ mm}$ und $297\text{ mm}$ soll das Netz der quadratischen Pyramide herausgeschnitten werden.

• Bestimme den prozentualen Anteil, der als Abfall übrigbleibt.

• Welche der folgenden Aussagen stimmt? Begründe deine Entscheidung. „Wenn man die Grundkante $a$ halbiert und die Körperhöhe $h_k$ verdoppelt,

[5 Pkt]

Zu jeder Funktionsgleichung gehören eine Wertetabelle und ein Graph.

• Ordne die Darstellungen einander zu.

• Ergänze die unvollständigen Darstellungen.

[5 Pkt]