Wahlteil B

Das Bild zeigt die Netze eines sechsseitigen und eines vierseitigen Spielwürfels.

Es werden Zufallsversuche durchgeführt.

Beide Würfel werden gleichzeitig geworfen und die Augenzahlen addiert.

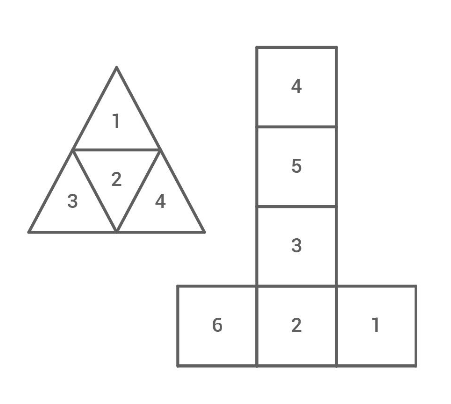
• Welche Augensummen werden am häufigsten gewürfelt? Begründe deine Entscheidung.

• Bestimme die prozentuale Wahrscheinlichkeit, dass beim Werfen der Würfel Folgendes passiert:

- Die Augensumme ist größer als 8 .

- Ein Würfel zeigt eine 4, der andere nicht.

[5 Pkt]

Die Abbildung zeigt einen kegelförmigen Messbecher mit einem Durchmesser $d=10\text{ cm}d=10\backslash cm$ und dem Winkel $\alpha ={\mathrm{38,5}}^{\circ }\backslash alpha=38\{,\}5^\backslash circ$.

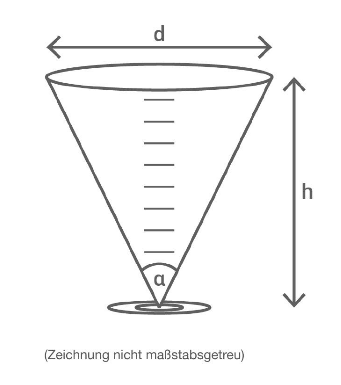
• Zeige, dass gilt: $h={\displaystyle \frac{\frac{d}{2}}{\tan \left(\frac{\alpha }{2}\right)}}h=\backslash dfrac\{\backslash frac\{d\}\{2\}\}\{\backslash tan\backslash left(\backslash frac\{\backslash alpha\}\{2\}\backslash right)\}$

Mit dem Messbecher soll Mehl abgemessen werden.

$1{\text{ cm}}^{3}1\backslash cm^3$ Mehl hat ein Gewicht von $\mathrm{0,6}\text{g}0\{,\}6\backslash text\{\backslash ,g\}$.

• Berechne, wie viel Gramm Mehl maximal in den Messbecher passen.

Ein regelmäßiges Zwölfeck ist von seinem Umkreis mit einem Radius von $8\text{ cm}8\backslash cm$ umgeben.

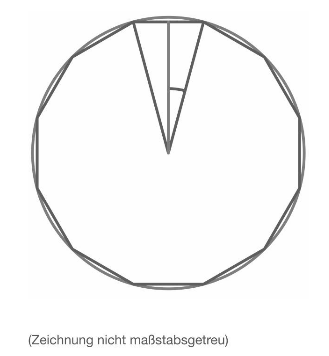
• Zeige, dass der markierte Winkel ${15}^{\circ }15^\backslash circ$ beträgt.

• Berechne den Umfang des Zwölfecks.

[5 Pkt]

Die Abbildung zeigt eine quadratische Pyramide.

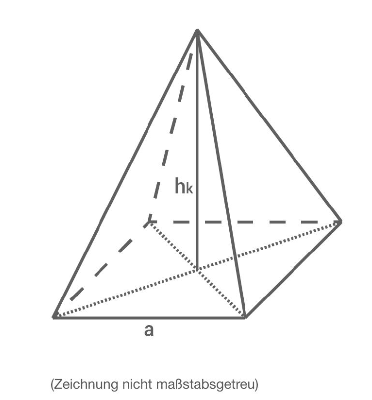
Es gilt:

$V=\mathrm{70,58}{\mathrm{c}\mathrm{m}}^{3}V=70\{,\}58\; \backslash mathrm\{~cm\}^\{3\}$ $h_k=7\mathrm{c}\mathrm{m}h\_\{k\}=7\; \backslash mathrm\{~cm\}$

• Zeige rechnerisch, dass die Grundkante der Pyramide $\mathrm{5,5}\text{ cm}5\{,\}5\backslash cm$ lang ist.

Aus einem DIN A4 - Blatt mit den Maßen $210\text{ mm}210\backslash mm$ und $297\text{ mm}297\backslash mm$ soll das Netz der quadratischen Pyramide herausgeschnitten werden.

• Bestimme den prozentualen Anteil, der als Abfall übrigbleibt.

• Welche der folgenden Aussagen stimmt? Begründe deine Entscheidung. „Wenn man die Grundkante $aa$ halbiert und die Körperhöhe $h_{k}h\_\{k\}$ verdoppelt,

[5 Pkt]

Zu jeder Funktionsgleichung gehören eine Wertetabelle und ein Graph.

• Ordne die Darstellungen einander zu.

• Ergänze die unvollständigen Darstellungen.

[5 Pkt]

An einem Drachen ist eine Schnur mit vier unterschiedlich farbigen Schleifen befestigt.

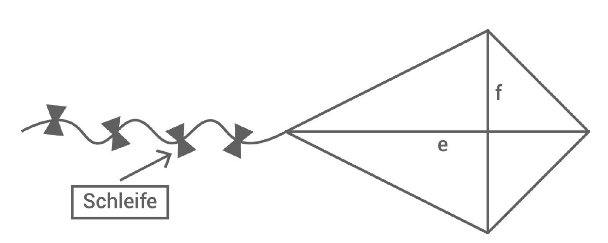
• Bestimme die Anzahl der verschiedenen Anordnungsmöglichkeiten der Schleifen.

In einem Karton befinden sich $150150$ Schleifen. ${\displaystyle \frac{1}{5}}\backslash dfrac\{1\}\{5\}$ davon sind rot und $1212$ sind gelb. Der Rest der Schleifen ist blau. Es wird zweimal blind ohne Zurücklegen gezogen.

• Bestimme, mit welcher prozentualen Wahrscheinlichkeit zwei blaue Schleifen gezogen werden.

Ein Drachenviereck hat einen Flächeninhalt von $\mathrm{1,35}{\mathrm{m}}^{2}1\{,\}35\; \backslash mathrm\{~m\}^\{2\}$. Die Diagonale $ee$ des Drachen ist um $20\mathrm{\%}20\; \backslash \%$ länger als die Diagonale $ff$.

• Bestimme die Längen der Diagonalen $ee$ und $ff$.

[5 Pkt]

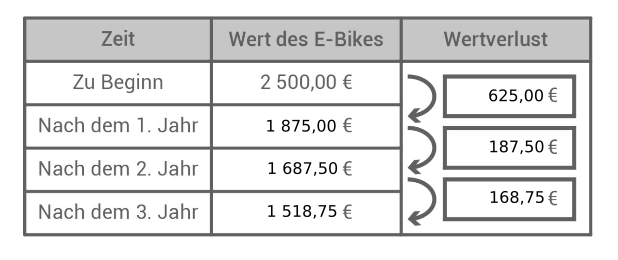
Lisa möchte ihr E-Bike (Neupreis: $\mathrm{2500,00}\text{€}2500\{,\}00\; €$ ) nach drei Jahren verkaufen. Im Internet liest sie, dass ein E-Bike im ersten Jahr $25\mathrm{\%}25\; \backslash \%$ und in den folgenden Jahren jeweils $10\mathrm{\%}10\; \backslash \%$ an Wert verliert.

• Bestimme, wie viel Euro das E-Bike nach drei Jahren noch wert ist.

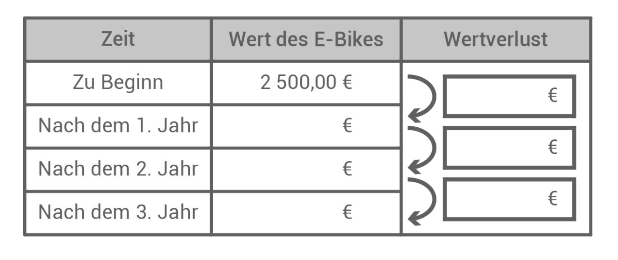
• Bestimme jeweils den Wertverlust pro Jahr.

• Erkläre, warum der Wertverlust in Euro jedes Jahr weniger wird.

Gegeben ist der Halbkreis über $\overline{AB}\backslash overline\{A\; B\}$ mit dem Mittelpunkt $MM$.

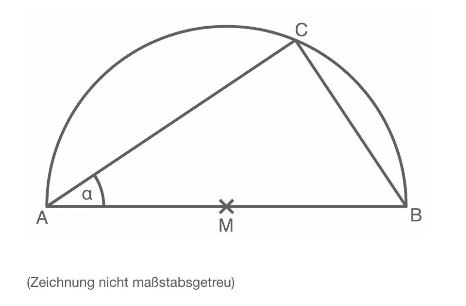
Es gilt: $\alpha ={50}^{\circ }\backslash alpha=50^\{\backslash circ\}$ $\overline{AC}=\mathrm{10,3}\mathrm{c}\mathrm{m}\backslash overline\{A\; C\}=10\{,\}3\; \backslash mathrm\{~cm\}$

• Berechne den Flächeninhalt des Halbkreises.

[5 Pkt]

Durch Vergrößerung des Dreiecks $ABCA\; B\; C$ entsteht das ähnliche Dreieck $A^{\mathrm{\prime }}{B}^{\mathrm{\prime }}{C}^{\mathrm{\prime }}A^\{\backslash prime\}\; B^\{\backslash prime\}\; C^\{\backslash prime\}$.

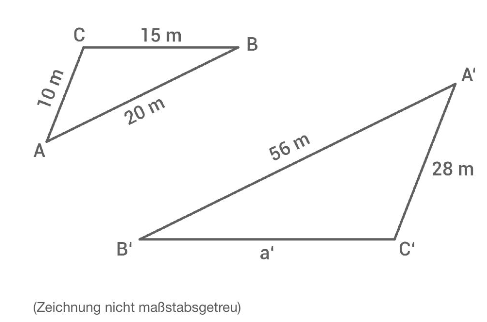
• Bestimme die Seitenlänge $a^{\mathrm{\prime }}a^\{\backslash prime\}$.

• Überprüfe folgende Aussage und begründe deine Entscheidung. „Alle gleichseitigen Dreiecke sind einander ähnlich".

Gegeben ist ein gleichschenkliges Dreieck $ABCA\; B\; C$ mit $\overline{AB}\backslash overline\{A\; B\}$ als Basis. Die Strecke $\overline{RT}\backslash overline\{R\; T\}$ ist parallel zur Basis.

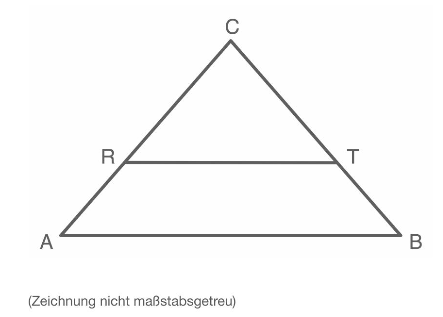
• Bestimmen Sie den Umfang des Dreiecks $RTCR\; T\; C$.

Es gilt:

• Zeige, dass gilt: "Wenn die Strecke $\overline{RT}\backslash overline\{R\; T\}$ halb so lang ist wie die Strecke $\overline{AB}\backslash overline\{A\; B\}$, dann ist auch der Umfang des Dreiecks $RTCR\; T\; C$ halb so groß wie der Umfang des Dreiecks $ABCA\; B\; C$."

[5 Pkt]

In einem Quader liegt der geschlossene Streckenzug $ACIFAA\; C\; I\; F\; A$. Der Winkel $\alpha \backslash alpha$ ist ${50}^{\circ }50^\{\backslash circ\}$ groß.

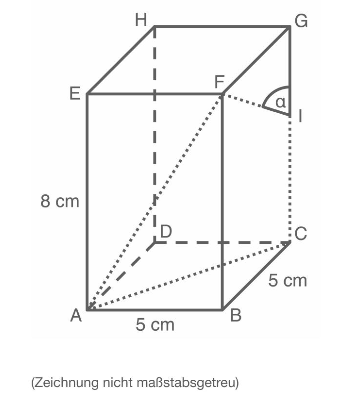
• Berechne die Länge des Streckenzuges.

• Löse die Gleichung: ${\displaystyle \frac{1}{4}}{x}^2-4(x+3)=24-4x\backslash dfrac\{1\}\{4\}\; x^\{2\}-4(x+3)=24-4\; x$

[5 Pkt]