Aufgaben - lernen mit Serlo!

Taschenrechnerfreier Teil

Gib an, mit welcher Wahrscheinlichkeit beide Schlüssel passen. (1 Pkt.)

Die Wahrscheinlichkeit, aus $5$ Wohnungsschlüsseln den Richtigen zu ziehen, ist $\frac{1}{5}$ .

Die Wahrscheinlichkeit, aus $5$ Briefkastenschlüsseln den Richtigen zu ziehen, ist $\frac{1}{5}$ .

$\Rightarrow P (zwei richtige Schlüssel) = \frac{1}{5} \cdot \frac{1}{5} = \frac{1}{25}$ .

Bestimme, mit welcher Wahrscheinlichkeit genau einer der beiden Schlüssel passt (1,5 Pkte.)

Ein Schlüssel passt nicht: $p = 1 - \frac{1}{5} = \frac{4}{5}$

Der erste Schlüssel passt: $P = \frac{1}{5} \cdot \frac{4}{5} = \frac{4}{25}$

Der zweite Schlüssel passt: $P = \frac{4}{5} \cdot \frac{1}{5} = \frac{4}{25}$

$\Rightarrow P (genau einer der beiden Schlüssel passt) = 2 \cdot \frac{4}{25} = \frac{8}{25}$ .

Gegeben sind gleichschenklige Dreiecke $A B_{n} C_{n}$ mit den Basen $A B_{n}$ .

Die Winkel $B_{n} A C_{n}$ haben das Maß $φ$ mit $φ \in] 0 °; 90 [$ .

Es gilt: $| A C_{n} | = 4 cm$ .

Die untenstehende Zeichnung zeigt das Dreieck $A B_{1} C_{1}$ für $φ = 40 °$ .

Ergänze in der Zeichnung zu A 2.0 das Dreieck $A B_{2} C_{2}$ für $φ = 75 °$ (1 Pkt.)

In den Dreiecken $A B_{n} C_{n}$ gilt für den Abstand $a$ der Punkte $C_{n}$ zur Geraden $A B_{n}$ : $a = x cm (x \in ℝ)$ .

Kreuzen Sie das passende Intervall für $x$ an. (1 Pkt.)

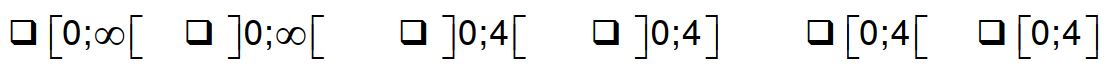
Es gilt: $φ \in] 0 °; 90 ° [$

Für $φ > 0$ ist dann der Abstand $a$ der Punkte $C_{n}$ zur Geraden $A B_{n}$ größer null. Die linke Intervallgrenze $0$ ist ein offenes Intervall.

Für $φ = 90 °$ ist der Abstand $a$ der Punkte $C_{n}$ zur Geraden $A B_{n}$ gleich $4$ .

Für $φ < 90 °$ ist der Abstand $a$ der Punkte $C_{n}$ zur Geraden $A B_{n}$ kleiner als $4$ . Die rechte Intervallgrenze $4$ ist ebenfalls ein offenes Intervall.

$\Rightarrow] 0; 4 [$ muss angekreuzt werden.

Die Dreiecke $A B_{n} C_{n}$ rotieren um die Gerade $A B_{n}$ .

Zeigen Sie, dass für den Oberflächeninhalt $O$ der entstehenden Rotationskörper in

Abhängigkeit von $φ$ gilt: $O = 32 \cdot π \cdot s i n φ {cm}^{2}$ . (2,5 Pkte.)

Der Rotationskörper besteht aus zwei gleich großen Kegeln.

Für den Kegelmantel gilt: $M = π \cdot r \cdot s$ . Dabei ist $s = | A C_{n} | = 4 cm$ die Mantellinie des Kegels und der Kegelradius ist $a$ .

$\Rightarrow O = 2 \cdot M = 2 \cdot π \cdot a \cdot | A C_{n} |$

Weiterhin gilt: $\sin φ = \frac{a}{4} \Rightarrow a (φ) = 4 \cdot \sin φ [cm]$

$\Rightarrow O = 2 \cdot π \cdot 4 \cdot \sin φ \cdot 4 = 32 \cdot π \cdot \sin φ [{cm}^{2}] ✓$

Durch Rotation des Dreiecks $A B_{3} C_{3}$ um die Gerade $A B_{3}$ entsteht ein Rotationskörper mit einem Oberflächeninhalt von $16 \cdot π {cm}^{2}$ .

Bestimmen Sie das zugehörige Maß für $φ$ . (1,5 Pkte.)

Löse die Gleichung $O = 16 \cdot π$ :

$16 \cdot π$	$=$	$32 \cdot π \cdot \sin φ$	$: (32 π)$
	↓	Löse nach $φ$ auf.
$\frac{1}{2}$	$=$	$\sin φ$

$φ = \sin^{- 1} (0,5) = 30 ° \Rightarrow L = {30 °}$

A 3.0 Die Skizze zeigt das rechtwinklige Dreieck $A B C$ mit der Hypotenuse $A B$ und dem
Schwerpunkt $S$ . Die Gerade $B S$ schneidet die Seite $A C$ im Punkt $M$ .
Es gilt: $| A C | = 8 \sqrt{3} cm$ ; $| B C | = 4 cm$ .
A 3.1 Begründen Sie ohne zu messen, dass der Punkt $M$ der Mittelpunkt der Strecke $A C$ ist. (1 Pkt.)
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der drei Seitenhalbierenden. Eine Seitenhalbierende verbindet einen Eckpunkt mit dem Mittelpunkt der gegenüberliegenden Seite. Hier ist der Punkt $S$ der Schwerpunkt des Dreiecks $A B C$ . Deshalb ist die Strecke $B M$ eine Seitenhalbierende $\Rightarrow$ der Punkt $M$ ist der Mittelpunkt der Strecke $A C$ .
A 3.2 Bestimmen Sie mithilfe einer Rechnung das Maß des Winkels $C B M$ . (2 Pkte.)
Es gilt: $\tan (∢ C B M) = \frac{\frac{1}{2} | A C |}{| B C |} = \frac{\frac{1}{2} \cdot 8 \cdot \sqrt{3}}{4} = \sqrt{3}$
$\Rightarrow ∢ C B M = \tan^{- 1} (\sqrt{3}) = 60 °$
Das Maß des Winkels $C B M$ beträgt $60 °$ .
Taschenrechner Teil
B 1.0 Fünftklässler bemalen für die Abschlussprüflinge ihrer Schule kleine Schachteln mit roter („r“), blauer („b“), grüner („g“) oder weißer („w“) Farbe und befüllen jede Schachtel mit einer Süßigkeit. Für die Befüllung stehen Süßigkeiten in den drei Geschmacksrichtungen Apfel („A“), Birne („B“) oder Mango („M“) zur Verfügung.
Das Baumdiagramm zeigt entsprechende Anteile. Es gilt: $p \in ℝ^{+}$ .
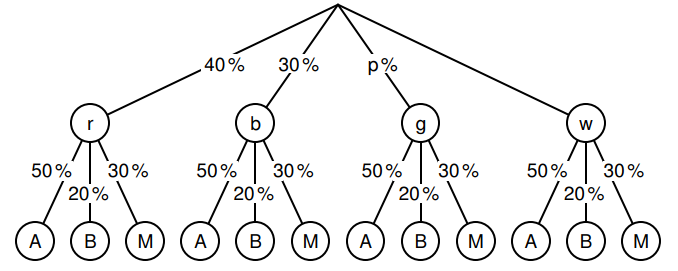
B 1.1 Kreuzen Sie den Anteil der weißen Schachteln an. (1 Pkt.)
$p (rot) = 40 %, p (blau) = 30 %, p (grün) = p % \Rightarrow p (weiß) = 1 - (40 % + 30 % + p %)$
$p (weiß) = 1 - (70 % + p %) = 1 - \frac{70 + p}{100}$ , kreuze entsprechend an.
B 1.2 Vor dem Prüfungsraum gibt eine Lehrkraft jedem Prüfling eine zufällig ausgewählte Schachtel. Die Wahrscheinlichkeit dafür, dass die erste ausgegebene Schachtel grün ist und eine Süßigkeit in der Geschmacksrichtung Apfel enthält, beträgt $10 %$ .
Berechnen Sie den Anteil $p %$ der grünen Schachteln. (1,5 Pkte.)
Es gilt: $\frac{p}{100} \cdot \frac{50}{100} = \frac{10}{100} \Rightarrow \frac{p}{100} = \frac{10}{50} = \frac{20}{100} \Rightarrow p % = 20 %$
Der Anteil $p %$ der grünen Schachteln beträgt $20 %$ .
B 1.3 Sebastian wünscht sich eine rote oder eine blaue Schachtel mit einer Süßigkeit, die nicht die Geschmacksrichtung Birne hat. Er vermutet, dass die erste ausgegebene Schachtel mit einer Wahrscheinlichkeit von mehr als $50 %$ seinem Wunsch entspricht.
Beurteilen Sie diese Vermutung. (2,5 Pkte.)
Nicht die Geschmacksrichtung Birne $\Rightarrow$ Apfel oder Mango
Rote Schachtel $\Rightarrow p = 40 %$ , blaue Schachtel $\Rightarrow p = 30 %$ .
Damit gilt:
$\underset{rot und A}{\underset{⏟}{\frac{40}{100} \cdot \frac{50}{100}}} + \underset{rot und M}{\underset{⏟}{\frac{40}{100} \cdot \frac{30}{100}}} + \underset{blau und A}{\underset{⏟}{\frac{30}{100} \cdot \frac{50}{100}}} + \underset{blau und M}{\underset{⏟}{\frac{30}{100} \cdot \frac{30}{100}}} = \frac{2000 + 1200 + 1500 + 900}{10000} = \frac{5600}{10000} = \frac{56}{100}$
Wegen $\frac{56}{100} > 50 %$ trifft Sebastians Vermutung zu.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Taschenrechnerfreier Teil

Gib an, mit welcher Wahrscheinlichkeit beide Schlüssel passen. (1 Pkt.)

Bestimme, mit welcher Wahrscheinlichkeit genau einer der beiden Schlüssel passt (1,5 Pkte.)

Taschenrechner Teil