Aufgaben
- 1
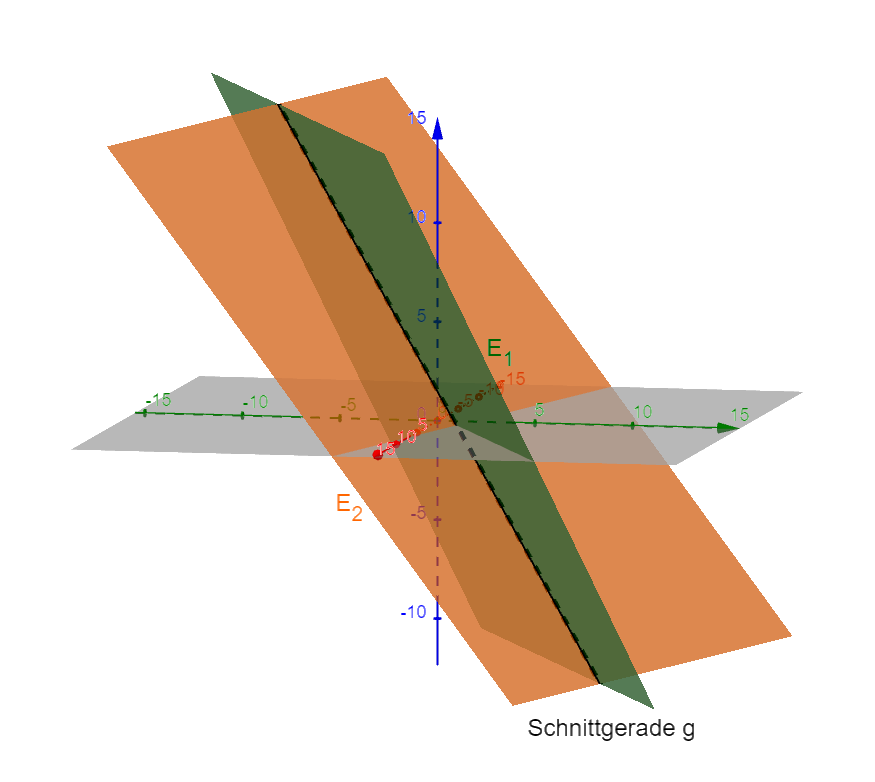
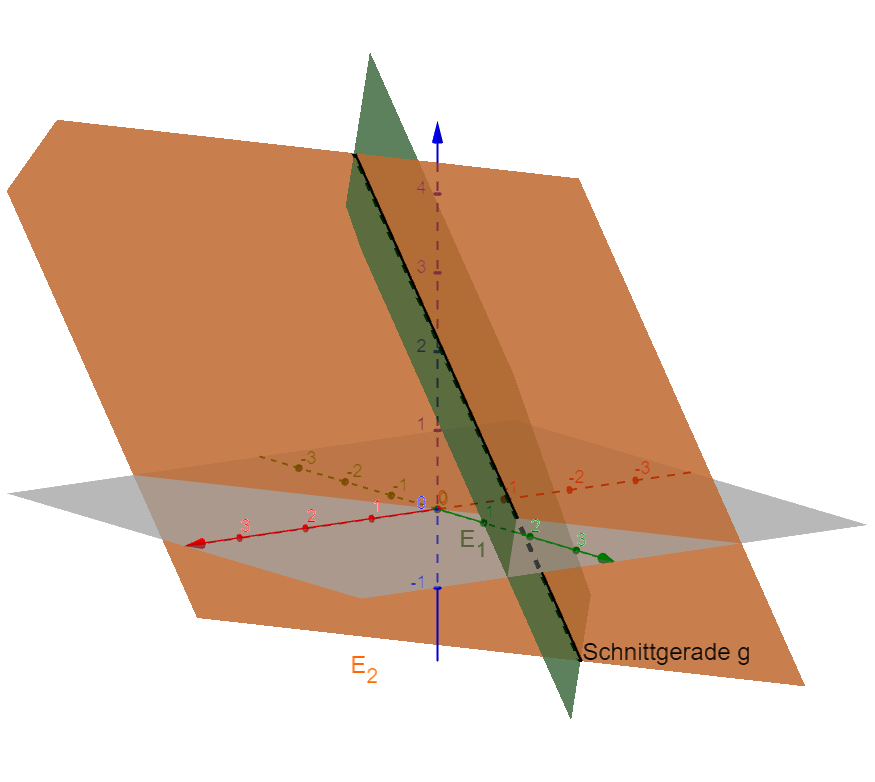
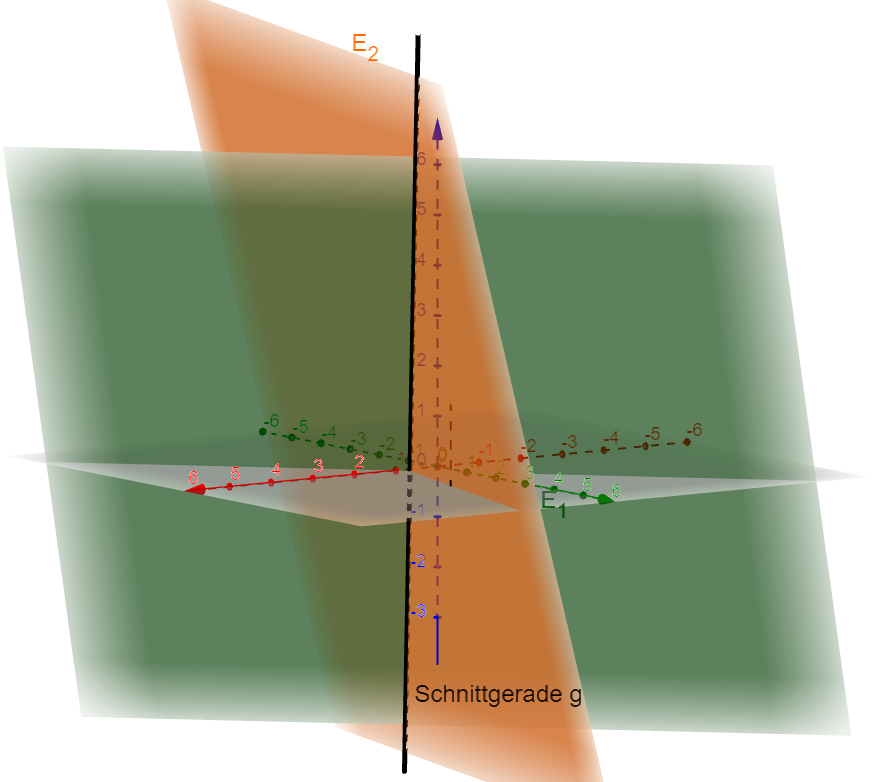
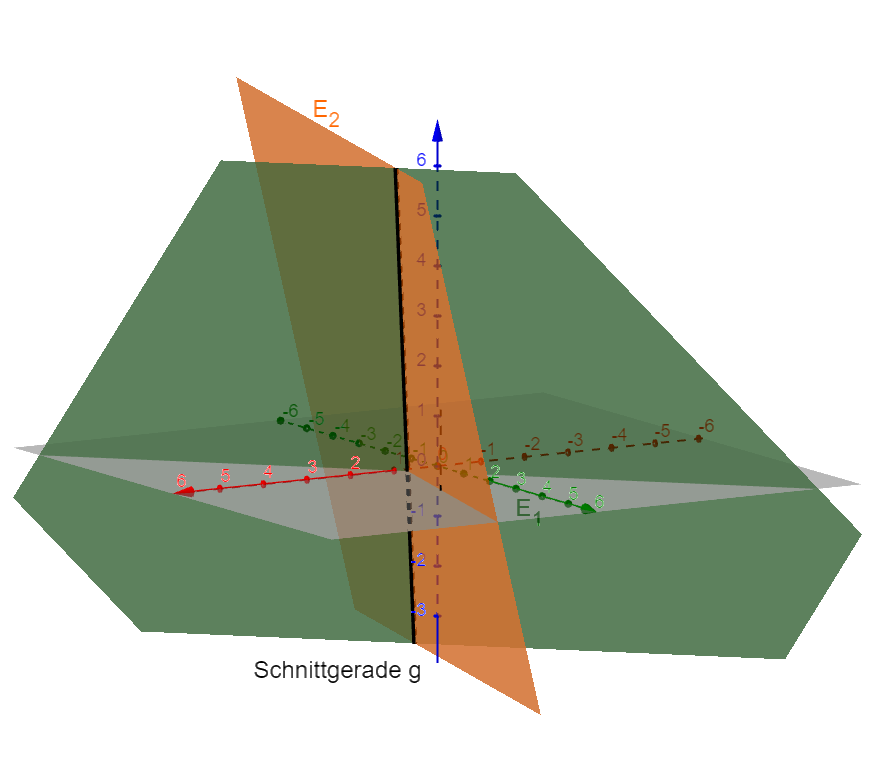
Gegenseitige Lage von Geraden und Ebenen
- 2
Axialschnitt eines Rotationskörpers
Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.
Die folgende Tabelle zeigt die Zuordnung zwischen einem Rotationskörper und dem dazugehörenden Axialschnitt.
Rotationskörper
Axialschnitt
Zylinder
Rechteck
Kegel
gleichschenkliges Dreieck
Kugel
Kreis
Halbkugel
Halbkreis
Kegelstumpf
gleichschenkliges Trapez

Wenn du lernen willst wie man einen Rotationskörper auf das Papier zeichnet, gehe auf den Artikel Skizzieren eines Rotationskörpers - Anleitung.
- 3
Für jedes ist die Funktionenschar gegeben durch .
Der Graph der Funktion ist .
Gib bei allen Teilaufgaben die Ergebnisse in Abhängigkeit vom Scharparameter an.
1. Wo schneiden die Scharkurven die -Achse?
2. Untersuche auf Hoch- und Tiefpunkte.
3. Bestimme das Verhalten der Funktion für und für und gib gegebenenfalls die Asymptote an.
4. Skizziere für und die Graphen von und von .
5. Welche Scharkurve hat für ein Extremum?
6. Auf welcher Ortskurve liegen die Extrema?
- 4
Gegeben sind die beiden windschiefen Geraden und
Berechne ihren Abstand und die beiden Lotfußpunkte auf den Geraden.
Hinweis: Verwende bei der Lösung dieser Aufgabe die Differentialrechnung.
- 5
Bestimme den Abstand zweier Ebenen mit Hilfe einer Lotgeraden.
- 6
Punkte in der Ebene
- 7
Testlösungen Abitur BW
- 8
Testlösungen Abitur BW (2)
- 9
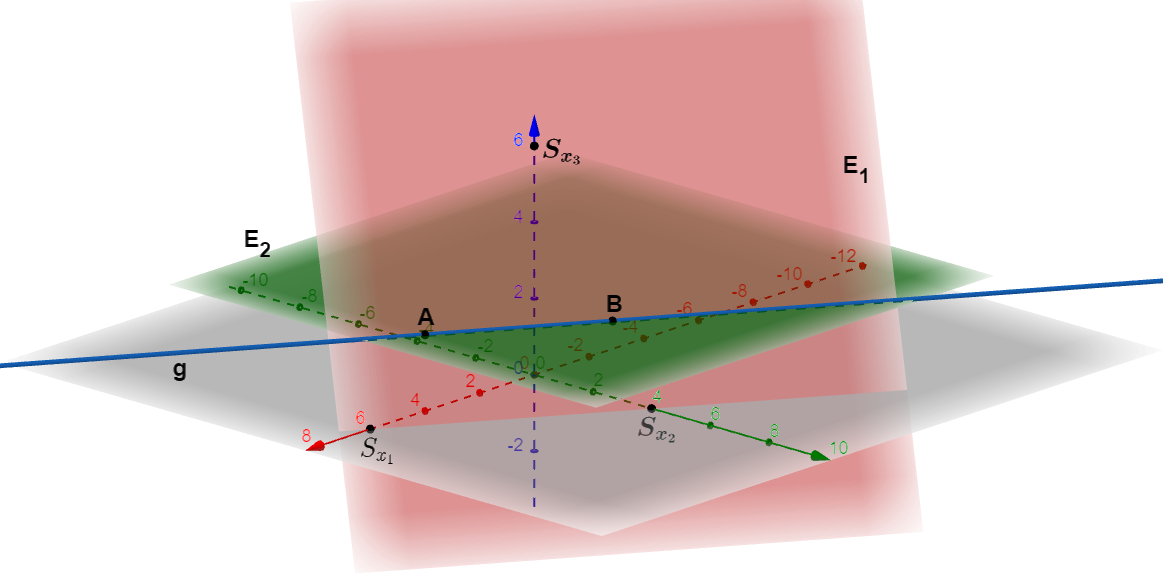
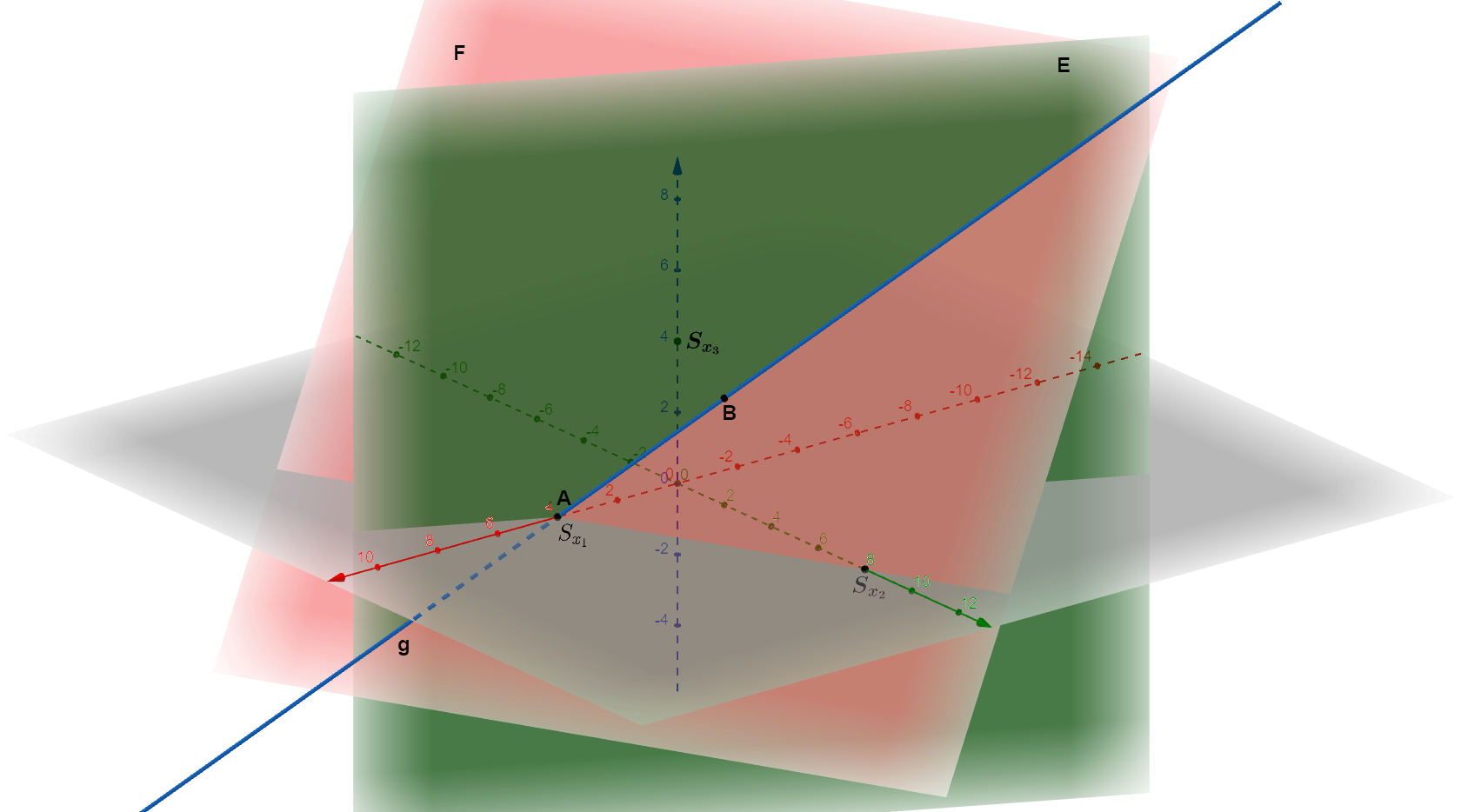
Spiegelung von 2 parallelen Ebenen
- 10
Kowalskys Testaufgabe
Lösung von Gleichungen-Übersicht
In einem Multiple-Choice-Test gibt es Aufgaben, bei denen man aus drei möglichen Lösungen die richtige ankreuzen muss. Felix hat sich nicht auf den Test vorbereitet. Mit welcher Wahrscheinlichkeit wird er trotzdem genau die Hälfte der Fragen richtig beantworten?
Gegeben ist der Kreis . Durch den Punkt verläuft eine Gerade , die Tangente an den Kreis sein soll. Berechne die Funktionsgleichung der Geraden und den Berührpunkt .
Welche Punkte sind Berührpunkte (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich nicht im Schnittpunkt)?
Gegeben ist ein Quader mit den Seiten , und .
Aus einer Quaderecke wird eine Pyramide herausgeschnitten. Die Schnitte verlaufen längs der Diagonalen der Seitenflächen.
a) Berechne jeweils die Flächeninhalte der vier Dreiecke , , und .
Hinweis: Verwende die Bezeichnungen von Bild 1 und Bild 3 und verwende für die Berechnung des Flächeninhalts von den Kosinussatz.
b) Weise nach, dass gilt.
Gegeben ist eine Ebenenschar mit .
a) Die beiden Ebenen und sollen senkrecht aufeinander stehen.
Welche Beziehung besteht zwischen und ?
b) Zu welcher Ebene aus der oben angegebenen Schar gibt es keine dazu senkrechte Ebene aus dieser Schar?
c) Es ist . Berechne den Abstand des Koordinatenursprungs von der Scharebene und gib gegebenenfalls den Grenzwert an.
Beziehungen zwischen den Winkelfunktionen
gegeben
gegeben
gegeben
Beziehungen zwischen Sinus, Kosinus, Tangens und Kotangens
- 11
Entscheide anhand des Graphens, ob der gegebene Graph der Funktion
achsensymmetrisch zur y-Achse oder
punktsymmetrisch zum Koordinatenursprung
ist.
- 12
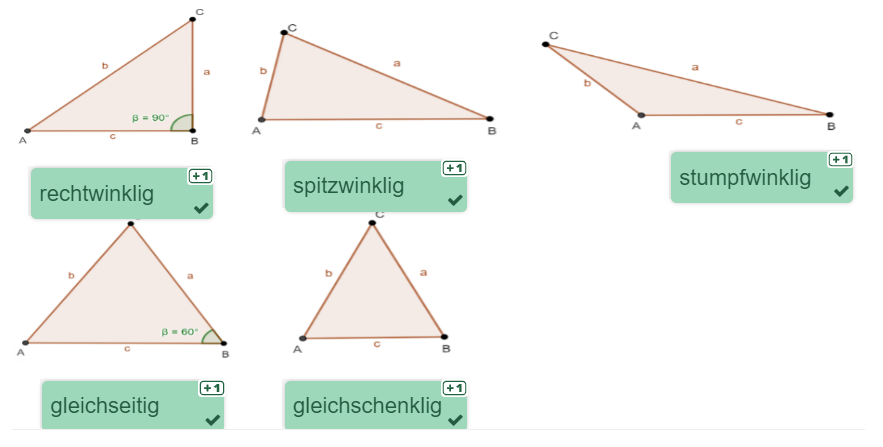
Entscheide graphisch, welche der jeweils angegebenen Aussagen auf den Graphen zutrifft.
- 13
Kowalskys zweite Testaufgabe
Test
Die Koordinatenform der Geradengleichung lautet:
Wenn Punkte und auf der Geraden gegeben sind, kann man die Parameter der Koordinatenform wie folgt berechnen:
Wie kommt man auf diese Berechnung der drei Parameter und ?
- 14
Prozentrechnung im Sandkasten
Im Sandkasten sind 20% der Fläche mit Spielzeug bedeckt. Wenn der Sandkasten insgesamt eine Fläche von hat, wie groß ist die Fläche, die mit Spielzeug bedeckt ist?
- 15
Anwendung des Strahlensatzes
Ein Baum wirft einen 4,5 m langen Schatten, während ein 1,2 m hoher Pfosten im selben Licht einen 1,6 m langen Schatten wirft. Wie hoch ist der Baum?
- 16
Single-Choice-Aufgabe zur Kurvendiskussion des Medikamentenabbaus
Betrachten Sie die Funktion , die den Medikamentenabbau im Körper über die Zeit beschreibt. Wie groß ist die momentane Änderungsrate des Medikamentenabbaus zum Zeitpunkt ?
- 17
Kurvendiskussion einer Exponentialfunktion
Bestimme die Nullstelle der Funktion .
Ermittle das lokale Extremum der Funktion .
Finde den Wendepunkt der Funktion .
Bestimme das asymptotische Verhalten der Funktion für .
Wie verhält sich der Graph der Funktion im Unendlichen?
- 18
Kurvendiskussion einer e-Funktion
Welche Art von Extrempunkt hat die Funktion bei ?
- 19
NRW 2024
Aufgabe 1
Ein Fan des VfL Bochum möchte mit einem mathematischen Modell den Besucheransturm beim nächsten Heimspiel beschreiben. Der Ansturm der Besucher wird (in Tausend Zuschauern pro Stunde) näherungsweise beschrieben durch die Funktion mit . Dabei stellt den Zeitpunkt der Öffnung des Stadions um 14.00 Uhr dar. Das Spiel wird anderthalb Stunden später angepfiffen, also bei .
Geben Sie an, wie groß der Besucheransturm um 14.15 Uhr und um 15.00 Uhr ist. Rechnen Sie das Ergebnis auch in Besucher pro Minute um.
Berechnen Sie, zu welchem Zeitpunkt der Besucheransturm am größten ist.
(zur Kontrolle: )
Beschreiben Sie, mit welchen Transformationen der Graph der Ableitungsfunktion aus dem Graphen der Funktion entsteht.
- 20
NRW 2024
Aufgabe 2
Gegeben ist die ganzrationale Funktion mit , .
Zeigen Sie, dass der Graph der Funktion punktsymmetrisch ist.
Durch den Tief- und den Hochpunkt des Graphen werden Geraden gezeichnet, die parallel zu den Achsen verlaufen; diese schließen dann mit den Achsen des Koordinatensystems eine rechteckige Fläche ein. Für welchen Parameterwert ergibt sich ein Quadrat?
- 21
NRW 2024
Aufgabe 3
Die Funktion f ist gegeben durch .
Zeigen Sie, dass die Tangente im Punkt an den Graphen der Funktion durch die Gleichung beschrieben werden kann.
Zeigen Sie, dass die Tangente und der Graph von auch den Punkt gemeinsam haben.
Fertigen Sie zu a), b) eine Skizze an.
Bestimmen Sie den Flächeninhalt des Dreiecks, das durch die y-Achse, die x-Achse und die Tangente eingeschlossen wird.
Bestimmen Sie den Flächeninhalt der Fläche, die von den Graphen von und eingeschlossen wird.
- 22
A 1.0 Die Funktion hat die Gleichung mit .
A 1.1 Bestimmen Sie die nach y aufgelöste Gleichung der Umkehrfunktion zu .
A 1.2 Der Graph der Funktion wird durch Parallelverschiebung mit dem Vektor
auf den Graphen der Funktion abgebildet, wobei der Punkt auf dem Graphen zu liegt.
- 23
Pflichtteil Teil A
Aufgabe 1
Gegeben ist die Funktion mit .
Weise nach: . (2 P)
Untersuche die Funktion auf lokale Extremstellen. (3 P)
- 24
Aufgabe 1
Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in definierten Funktion modellhaft beschreiben. Dabei ist die Zeit in Minuten, die seit der Entnahme aus dem Kühlschrank vergangen ist, und die Wassertemperatur in . Die Raumtemperatur beträgt konstant .
(i) Geben Sie die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an. (1 P)
(ii) Bestimmen Sie den Zeitpunkt, zu dem die Wassertemperatur beträgt. (2 P)
Berechnen Sie die Werte der folgenden Terme und interpretieren Sie diese im Sachzusammenhang:
(i) (2 P)(ii) (3 P)
Zeigen Sie, dass in diesem Modell gilt:
Es gibt eine Konstante , sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das -fache der momentanen Änderungsrate der Wassertemperatur ist. (4 P)
Die folgende Rechnung stellt die Lösung einer Aufgabe im vorliegenden Sachzusammenhang dar:
Aus ergibt sich .
Formulieren Sie eine passende Aufgabenstellung. (3 P)
- 25
Bei einem Glücksspielautomaten gewinnt man, wenn die gleichen
Symbole in der gleichen Farbe angezeigt werden.

Die Wahrscheinlichkeit zu gewinnen, ist bestimmt .
Eine der folgenden Aussagen ist richtig. Kreuze an.
/1P.
Oke soll aus den gegebenen Karten eine ziehen.
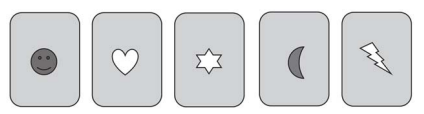
Formuliere eine Spielregel für das Ziehen einer Karte, so dass die
Gewinnchance größer als ist.
/1P.
- 26
Aufgabe 1
Gegeben ist eine in definierte Funktion , wobei eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von .
Abbildung 1
Zeigen Sie, dass eine Gleichung der ersten Ableitungsfunktion von ist.
Die beiden Tiefpunkte des Graphen von haben jeweils die y-Koordinate .
Ermitteln Sie den Wert von .
- 27
Aufgabe 2
Die Funktion ist gegeben durch .
Der Graph von ist in Abbildung 2 dargestellt.
Abbildung 2
Interpretieren Sie die Aussage in Bezug auf den Graphen von .
(2 P)
Berechnen Sie . (3 P)
- 28
an der Wendestelle..." oder "Im Wendepunkt mit der x-Koordinate x_0
r'(x) beschreibt die Änderung der Zuflussrate r(x).
Und die zweite Ableitung r''(x) beschreibt die Änderung der 1. Ableitung r'(x).
Und an der Wendestelle hat die 2. Ableitung den Wert Null. Das bedeutet, dass die Änderung der Zuflussrate gleich Null ist. Das heißt, hier sogar zeitlich, dass die Änderung der Zuflussrate vorher größer war und dann abnimmt. Die Änderung der Zuflussrate hat ihr Maximum erreicht.
Also die Stärke des Regens=Zuflussrate lässt nach.
Begründe, dass die einzige Nullstelle von ist
Gegeben ist .
Für die Nullstellen löse die Gleichung .
Weil für alle folgt mit dem Satz vom Nullprodukt:
Demnach ist die einzige Nullstelle.
Strategie
Die notwendige Bedingung für ein Extremum ist .
Bilde die 1. Ableitung und löse die Gleichung und .
Berechne die Funktionswerte an den Stellen und .
Die hinreichende Bedingung für ein Extremum ist .
Bilde die 2. Ableitung und prüfe mit den Werten und .
Gib die Koordinaten der Extrema an.
Untersuche rechnerisch auf lokale Extremstellen
Die notwendige Bedingung für ein Extremum ist .
Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung:
Weil für alle folgt mit dem Satz vom Nullprodukt:
Die hinreichende Bedingung für ein Extremum ist .
Bilde mithilfe der Produkt- und Kettenregel die 2. Ableitung:
Die Funktion hat genau eine lokale Extremstelle.
Der Graph von hat bei ein lokales Maximum.
Zeige rechnerisch, dass der Punkt ein Hochpunkt des Graphen von ist
Gegeben ist .
Berechne und :
Die notwendige Bedingung für ein Extremum ist .
Mit dem Satz vom Nullprodukt folgt:
Lokale Extremstellen sind also oder .
Nach Aufgabenstellung muss nur beachtet werden.
Die hinreichende Bedingung für ein Extremum ist .
Maximum
Berechne .
Der Punkt ist ein Hochpunkt des Graphen von .
Zeige rechnerisch, dass die Tangente an den Graphen von im Punkt parallel zur -Achse verläuft
Es ist und .
Im Punkt verläuft die Tangente an den Graphen von parallel zur -Achse.
Bestimme eine Gleichung der Geraden , die durch die beiden Wendepunkte des Graphen von verläuft
an der Wendestelle..." oder "Im Wendepunkt mit der x-Koordinate x_0
Berechne die Wendepunkte:
Die notwendige Bedingung für einen Wendepunkt ist .
Mit dem Satz vom Nullprodukt folgt:
Wendestellen liegen bei oder vor, wenn die hinreichende Bedingung erfüllt ist.
Berechne und
Die Bedingung ist erfüllt, d.h. Wendestellen liegen bei oder vor.
Berechne und .
Die Wendepunkte haben die Koordinaten und .
Für die Geradengleichung benutze die Zwei-Punkte-Form der Geradengleichung:
Die Gleichung der Geraden , die durch die beiden Wendepunkte des Graphen von verläuft, lautet .
Zeichne in die Abbildung eine Gerade ein, die parallel zu ist und für mit dem Graphen von genau einen Punkt gemeinsam hat
Berechne alle Schnittpunkte des Graphen mit den Koordinatenachsen
Gegeben ist .
Schnittpunkte mit der x-Achse:
Die Nullstelle der Funktion ist bekannt .
Führe eine Polynomdivision durch.
Löse nun die Gleichung mit der pq-Formel:
↓ Setze und ein.
Somit lauten die Schnittpunkte von mit der x-Achse und .
Schnittpunkt mit der y-Achse:
Setze in ein .
Der Schnittpunkt mit der y-Achse ist .
Ermittle Art und Koordinaten aller relativen Extrempunkte von
Aufg. 1 Teil 1: ohne Hilfsmittel – Analysis
Gegeben ist die Funktion mit der Definitionsmenge .
Ihr Graph in einem kartesischen Koordinatensystem wird mit bezeichnet.
a) Geben Sie die Gleichungen aller Asymptoten von und die Nullstelle von an.
(2 BE)
b) Weisen Sie nach, dass die Funktion in ihrer Definitionsmenge umkehrbar ist, und ermitteln Sie die Definitionsmenge der Umkehrfunktion von . (6 BE)
c) Der Graph von und die zur x-Achse senkrechte Gerade bei schließen zusammen mit der x-Achse im I. Quadranten ein Flächenstück ein.
Berechnen Sie die exakte Maßzahl des Flächeninhalts dieses Flächenstücks. (4 BE)
d) Gegeben ist nun die Funktion mit der maximalen Definitionsmenge . Ermitteln Sie die Definitionsmenge und die exakte Nullstelle von . (5 BE)
Aufg. 2 Teil 1: ohne Hilfsmittel – Analysis
Die nachfolgende Abbildung zeigt einen Ausschnitt des Graphen einer in stetigen Funktion . Die x-Achse ist Asymptote . Außerdem gilt: für .
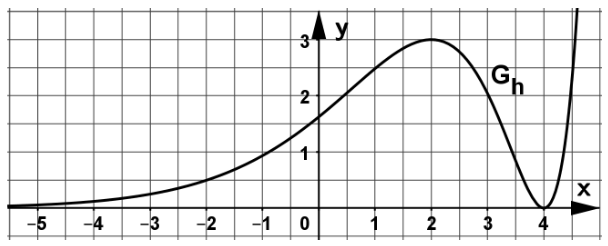
Zudem ist die Funktion mit der Definitionsmenge gegeben.
Entscheiden Sie für die beiden folgenden Aussagen jeweils, ob die Aussage wahr oder falsch ist, und begründen Sie Ihre Entscheidung.
A: „Der Graph von besitzt bei einen Extrempunkt.“
B: „Der Graph von hat bei eine Tangente mit einem positiven y-Achsenabschnitt.“
(5 BE)
Teil 2: mit Hilfsmitteln – Analysis I
1 Gegeben ist die Funktion mit der Definitionsmenge.
Der Graph von in einem kartesischen Koordinatensystem wird mit bezeichnet.
a) Berechnen Sie die Nullstelle von . Bestimmen Sie außerdem das Verhalten der
Funktionswerte von an den Rändern der Definitionsmenge und geben Sie die Gleichung der Asymptote von an. (7 BE)
b) Ermitteln Sie das Steigungsverhalten von und geben Sie die Wertemenge von an. (5 BE)
c) Bestimmen Sie die Koordinaten des Wendepunkts von .
Teil 2: mit Hilfsmitteln – Analysis I
2 Gegeben ist die Funktion mit der Definitionsmenge .
a) Zeigen Sie, dass der Graph der Funktion u streng monoton fallend ist. (4 BE)
b) Die Funktion ist umkehrbar (Nachweis nicht erforderlich). Ermitteln Sie einen Term der Umkehrfunktion von . (3 BE)
Teil 2: mit Hilfsmitteln – Analysis I
3 Gegeben sind die Funktionen und mit den jeweils maximalen Definitionsmengen und .
a) Bestimmen Sie die maximale Definitionsmenge von , sowie jeweils Art und
x-Koordinaten aller Extrempunkte des Graphen von . (7 BE)
b) Zeigen Sie, dass auch in der Form dargestellt werden kann. Ermitteln Sie anschließend eine integralfreie Darstellung von . (8 BE)
Teil 2: mit Hilfsmitteln – Analysis I
4 Weinkenner sind davon überzeugt, dass je nach Weinsorte die passende Weintemperatur wichtig für den Genuss des Weins ist. So soll zum Beispiel Rotwein bei Raumtemperatur genossen werden. Mit einem Wein-Thermometer wird in einem Raum die Temperatur des Weins gemessen, die niedriger als die Raumtemperatur ist. In dieser Aufgabe zeigt das Wein-Thermometer unmittelbar vor dem Eintauchen in den Wein die Raumtemperatur von an. Nach dem Eintauchen in den Wein wird es erst allmählich die Weintemperatur anzeigen. Sowohl die Raumtemperatur als auch die Weintemperatur sind während der Messung als konstant zu betrachten.
Die vom Wein-Thermometer in der Einheit angezeigte Temperatur in Abhängigkeit von der Zeit (gemessen in Sekunden ab dem Zeitpunkt des Eintauchens) lässt sich durch die Differenzialgleichung beschreiben, wobei ein reeller Parameter ist. Auf das Mitführen der Einheiten wird im Folgenden verzichtet.
Zeigen Sie, dass die Funktion für jeden Wert von eine Lösung der obigen Differenzialgleichung ist, und begründen Sie, warum in der vorliegenden Situation gelten muss. (4 BE)
Teil 2: mit Hilfsmitteln – Analysis II
1 Gegeben ist die Funktion mit der maximalen Definitionsmenge .
Der Graph von in einem kartesischen Koordinatensystem wird mit bezeichnet.
a) Zeigen Sie, dass ist, und berechnen Sie die Nullstellen von auf eine
Nachkommastelle genau. (6 BE)
b) Ermitteln Sie die Gleichungen aller Asymptoten von . (5 BE)
c) Ermitteln Sie die maximalen Monotonieintervalle von und bestimmen Sie damit Art und Koordinaten des Extrempunkts von .
(8 BE)
Teil 2: mit Hilfsmitteln – Analysis II
2 Nun wird die Funktion mit der Definitionsmenge betrachtet.
a) Ermitteln Sie ohne Verwendung einer integralfreien Darstellung von die Anzahl und die Lage der Nullstellen von . (3 BE)
b) Ermitteln Sie eine integralfreie Darstellung von h. (6 BE)
Teil 2: mit Hilfsmitteln – Analysis II
3.0 Gegeben ist die Funktion mit der Definitionsmenge . Der Graph von in einem kartesischen Koordinatensystem wird mit bezeichnet.
a) Begründen Sie für die folgenden Aussagen jeweils, ob sie wahr oder falsch sind.
A: „Der Graph von hat bei einen absoluten Extrempunkt.“
B: „Die Gerade mit der Gleichung ist Asymptote von .“
(6 BE)
b) Die Funktion ist umkehrbar (Nachweis ist nicht erforderlich). Die Tangente berührt den Graphen der Umkehrfunktion von im Punkt . Ermitteln Sie die Steigung der Tangente . (5 BE)
Teil 2: mit Hilfsmitteln – Analysis II
4 Auf einen bestimmten Körper wirkt zu jedem Zeitpunkt seit Beobachtungsbeginn eine konstante Kraft. Außerdem wirkt auf den Körper eine Reibungskraft, die proportional zum Quadrat der Momentangeschwindigkeit des Körpers ist. Es gilt modellhaft die Differenzialgleichung . Die Geschwindigkeit wird in , die Zeit in angegeben. Bei den folgenden Berechnungen darf auf das Mitführen der Einheiten verzichtet werden.
Untersuchen Sie, ob die Funktion v mit der Gleichung eine spezielle
Lösung der Differenzialgleichung ist. (4 BE)
Abitur Bayern 2025 Analysis m.H.
Gegeben ist die Funktion mit ihrer Definitionsmenge
Der Graph der Funktion wird mit bezeichnet.
a) Untersuchen Sie, ob eine Symmetrie zum Koordinatensystem besitzt. (3 BE)
b) Ermitteln Sie die exakten Nullstellen der ersten Ableitungsfunktion mit der Definitionsmenge .
c) Die nachfolgende Abbildung zeigt einen Ausschnitt des Graphens von der Funktion . Alle Nullstellen und Definitionslücken sind in der Abbildung ersichtlich. Geben Sie die maximalen Monotonieintervalle sowie jeweils die Art aller Extremstellen von an.
Hinweis: Anstelle der exakten Zahlenwerte können bei der Angabe der Intervalle die in der Abbildung ersichtlichen Bezeichnungen und verwendet werden.
Pol ohne
VZW
Pol ohne
VZW
Pol ohne
VZW
x
x_3
x_1
0
x_2
x_4
+
f'(x)
+
Def. lücke
+
0
-
Def. lücke
0
+
Def. lücke
G_f
HP
TP
d) Zeigen Sie, dass die Funktion auch durch die Gleichung dargestellt werden kann und berechnen Sie das bestimmte Integral . (7 BE)
2. Bei der Milchsäuregärung wandeln Bakterien die in der Milch befindliche Laktose in Milchsäure um. Die Funktion mit und gibt die Milchsäurekonzentration in Abhängigkeit von der Zeit an. Dabei wird in Gramm pro Liter gemessen und gibt die Zeit in Stunden an, die seit Beobachtungsbeginn vergangen ist. Bei Rechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf eine Nachkommastelle.
a) In einem Laborversuch wird die Milchsäurekonzentration von einem Liter Milch stündlich gemessen. Zu Beobachtungsbeginn beträgt die Milchsäurekonzentration Gramm pro Liter und Stunden nach Beobachtungsbeginn Gramm pro Liter. Berechnen Sie die Werte der Parameter und so, dass die Modellfunktion mit diesen beiden Messwerten in Einklang steht. (3 BE)
b) Im Folgenden gilt und . Somit ergibt sich mit . Der Graph von wird mit bezeichnet.
1. Zeigen Sie, dass die Milchsäurekonzentration nach diesem Modell stetig zunimmt.
[ Mögliches Teilergebnis ] (4 BE)
2. Für die zweite Ableitungsfunktion gilt mit . (Nachweis nicht erforderlich.)
Ermitteln Sie den Zeitpunkt , zu dem die erste Ableitungsfunktion ein absolutes Maximum besitzt. Berechnen Sie die Differenz und interpretieren Sie diesen Wert im Sachzusammenhang. (6 BE)
3. Zeichne Sie im Bereich in ein Koordinatensystem. Wählen Sie auf beiden Achsen einen geeigneten Maßstab. Kennzeichnen Sie auch die Differenz in Ihrer Abbildung. (4 BE)
4. Weisen Sie nach, dass die Funktion mit der Definitionsmenge eine Stammfunktion von ist. (3 BE)
5. Die durchschnittliche Milchsäurekonzentration in über einen Zeitraum in Stunden beträgt .
Berechnen Sie die Milchsäurekonzentration in dieser Milchprobe in den ersten sechs Beobachtungsstunden. (3 BE)
aus
Analytische Geometrie
1 In einem kartesischen Koordinatensystem sind die Punkte , und gegeben.
Runden Sie Ihre Endergebnisse gegebenenfalls auf eine Nachkommastelle.
a) Bestimmen Sie die Lösungsmenge der Gleichung mit und interpretieren Sie Ihr Ergebnis geometrisch. (6 BE)
b) Berechnen Sie die Maßzahl des Flächeninhaltes des Dreiecks . (3 BE)
c) Die Gerade verläuft durch die Punkte und .
Es gilt: . (Nachweis nicht erforderlich!)
Berechnen Sie den Abstand der Geraden zum Punkt . (5 BE)
2
Zu FOS 2022 Aufg.2 Alternative
Nach Aufgabe b) gilt: Der Nenner der 1. Ableitung ist die Gleichung einer nach oben geöffneten Parabel mit Scheitelpunkt .
Da ist, hat die 1. Ableitung bei einen Hochpunkt bei ist dann Wendepunkt.
Die Koordinaten des Wendepunkts von sind .
- 29
Herr Malinowski sieht auf seiner App der Gasverbrauch pro Tag in innerhalb einer Woche.
Er denkt darüber nach, welche mathematische Funktion den Gasverbrauch beschreiben kann und vermutet, dass es sich um eine e-Funktion handeln könnte.
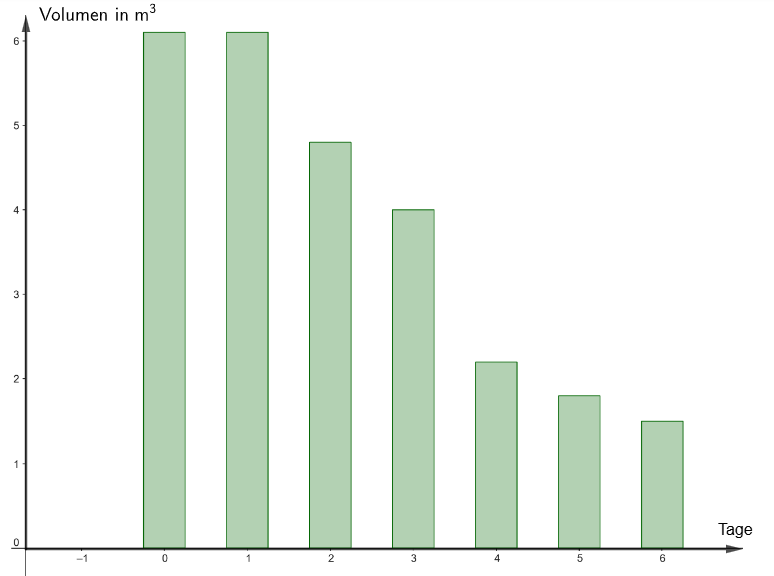
Abbildung
Die zur Abbildung gehörenden Daten findest Du in der folgenden Tabelle.
x in
Tagen
y in
0
6,1
1
6,1
2
4,8
3
4
4
2,2
5
1,8
6
1,5
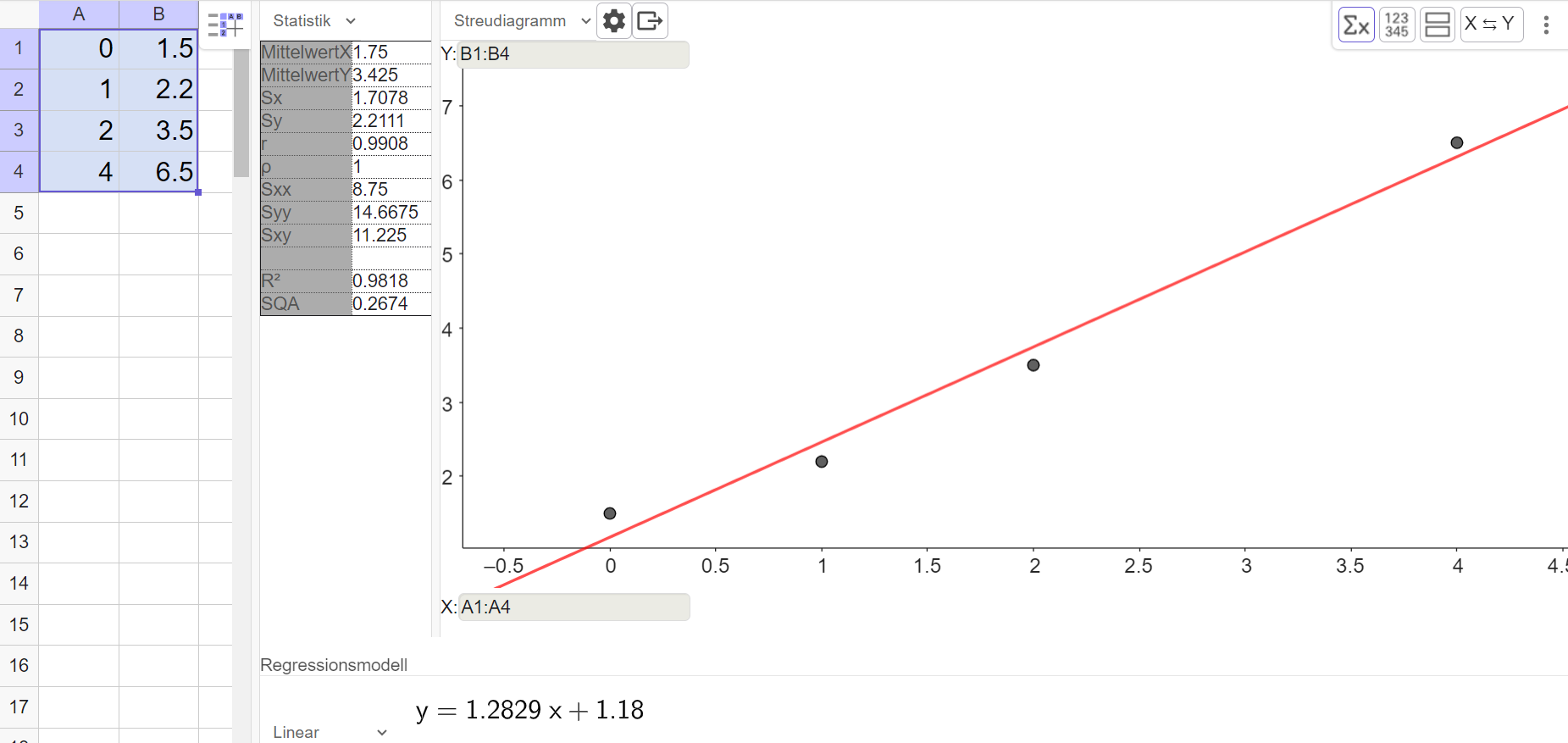
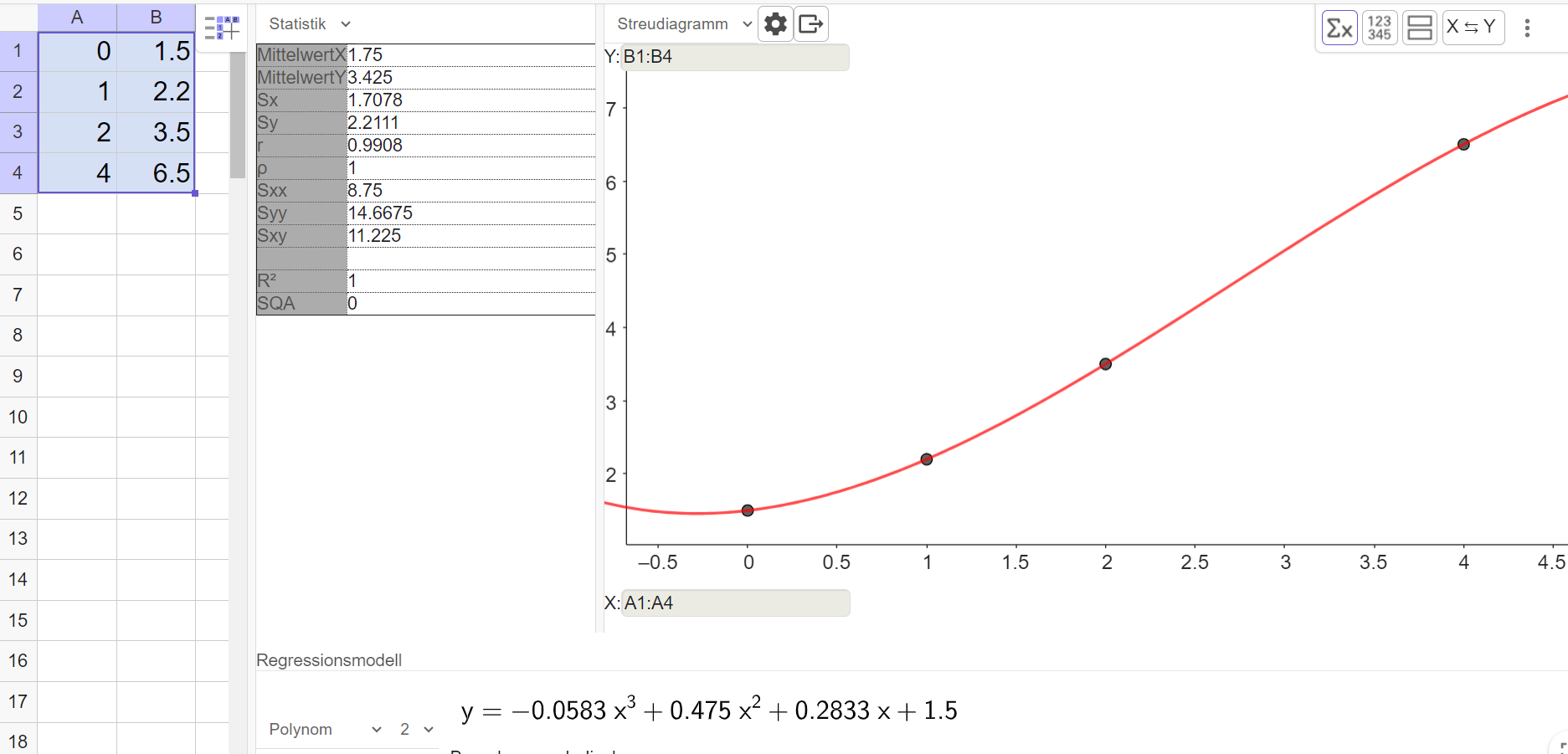
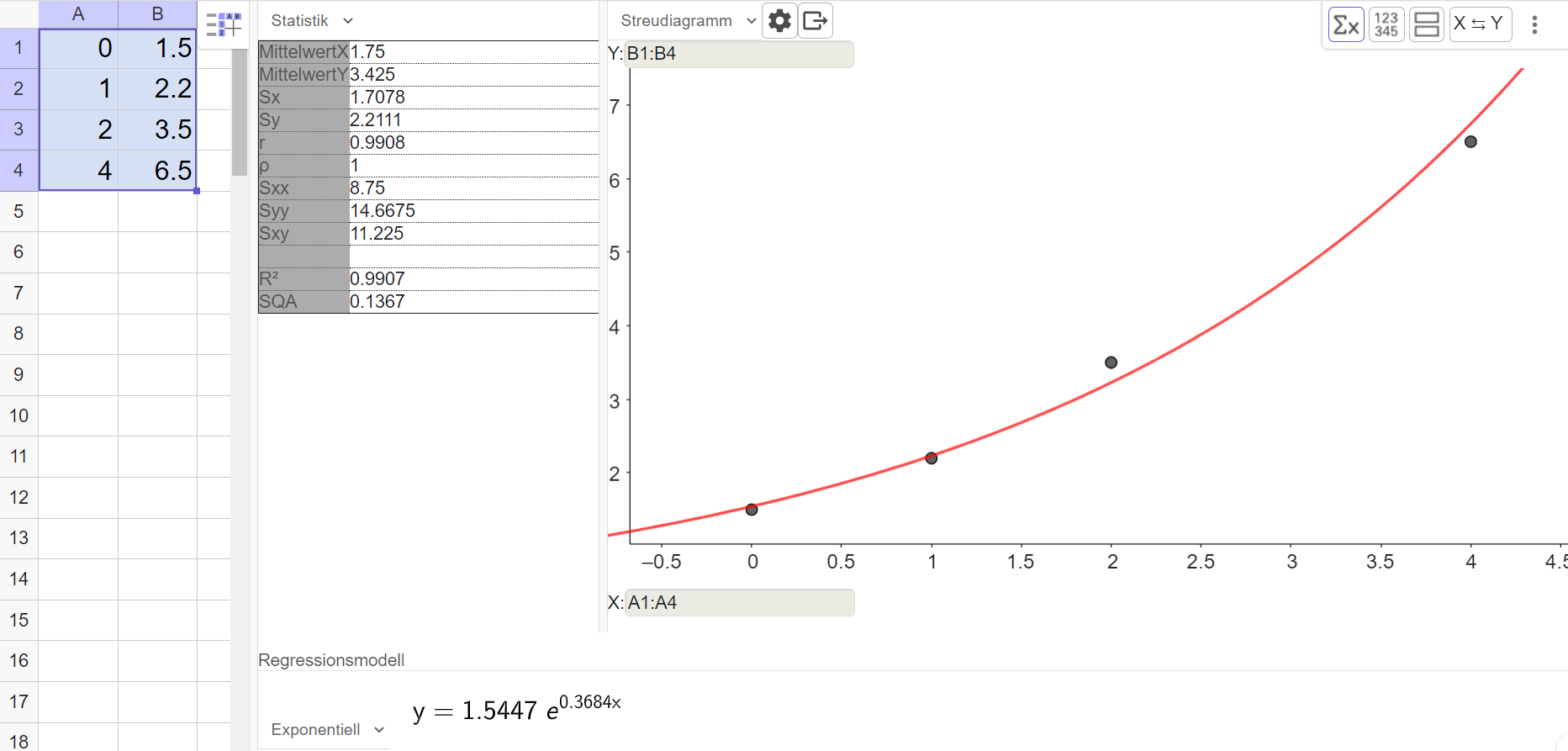
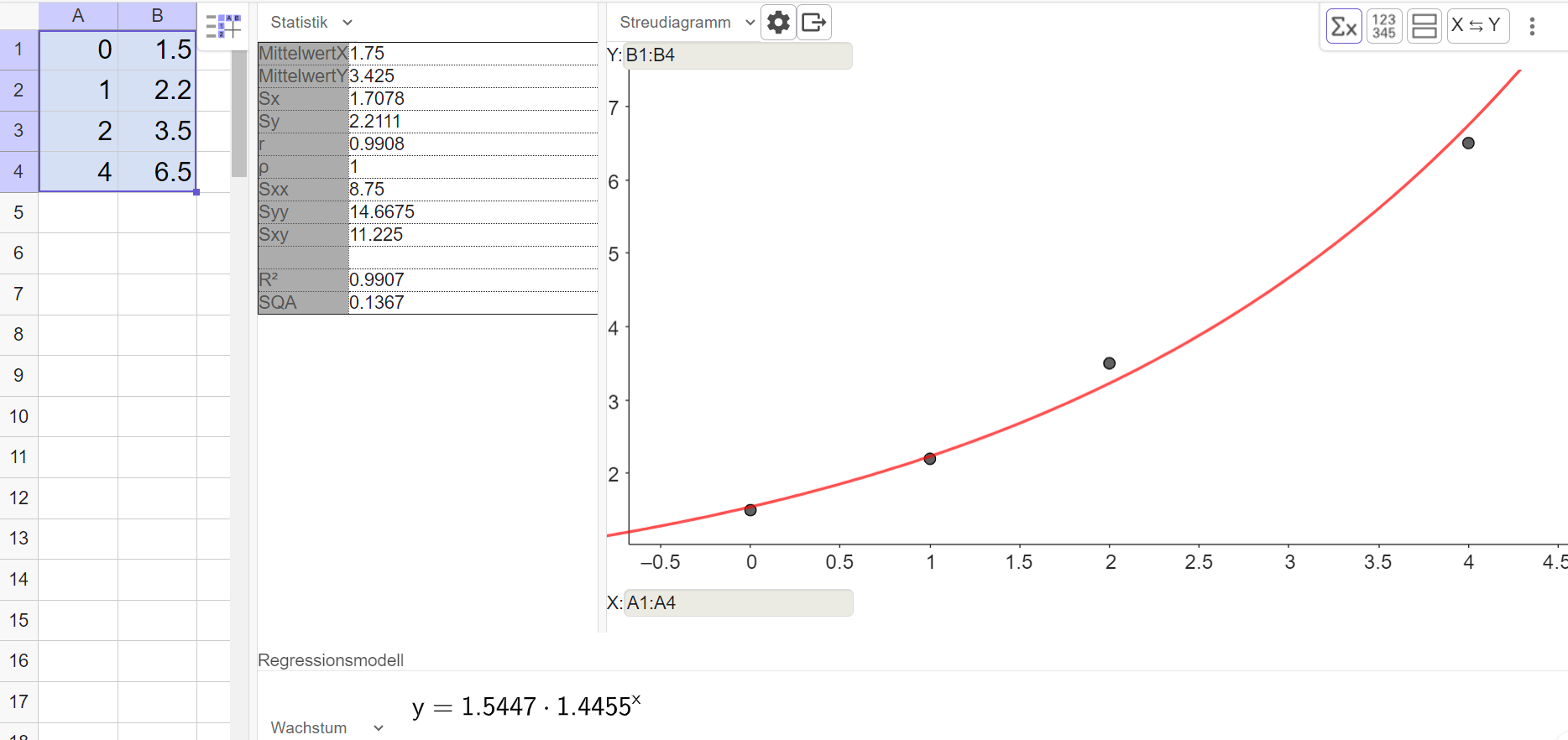
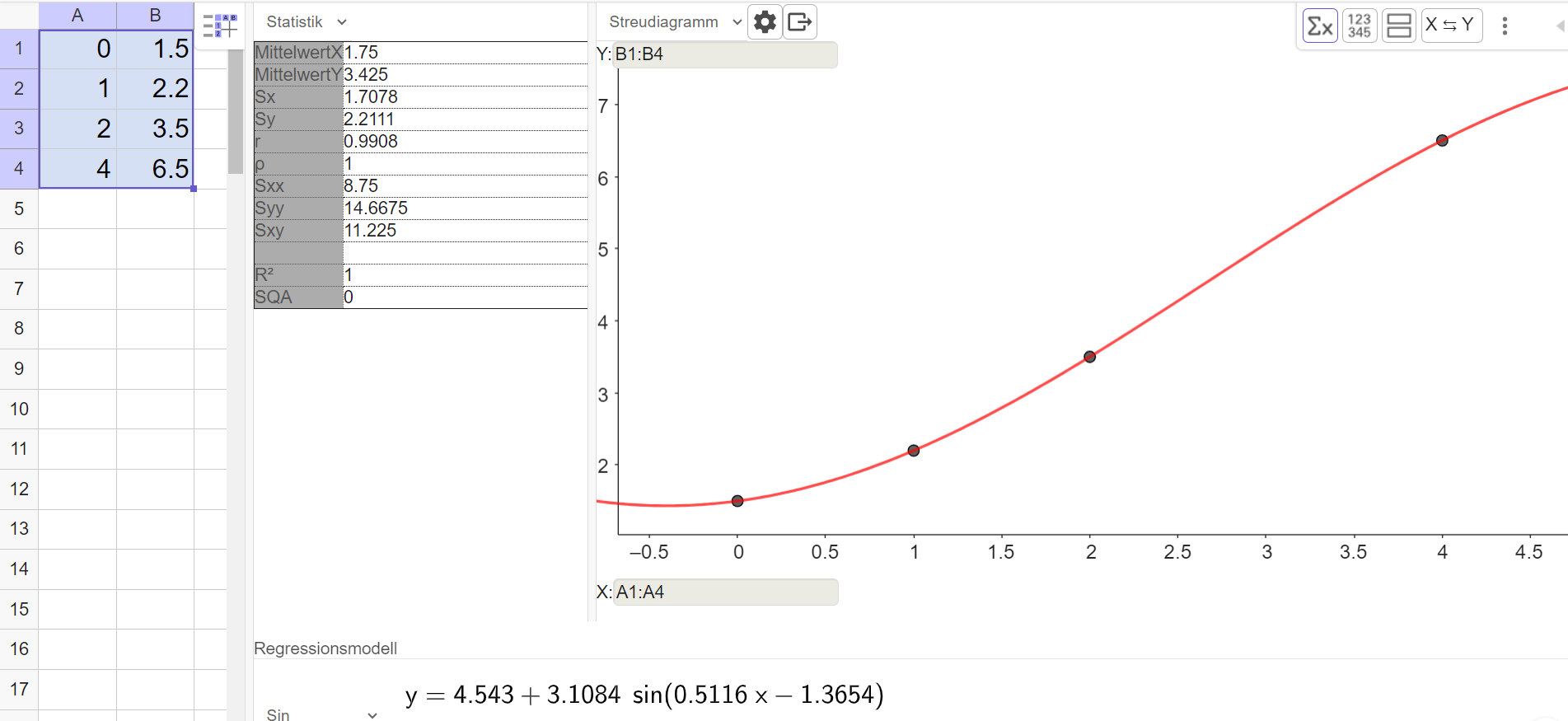
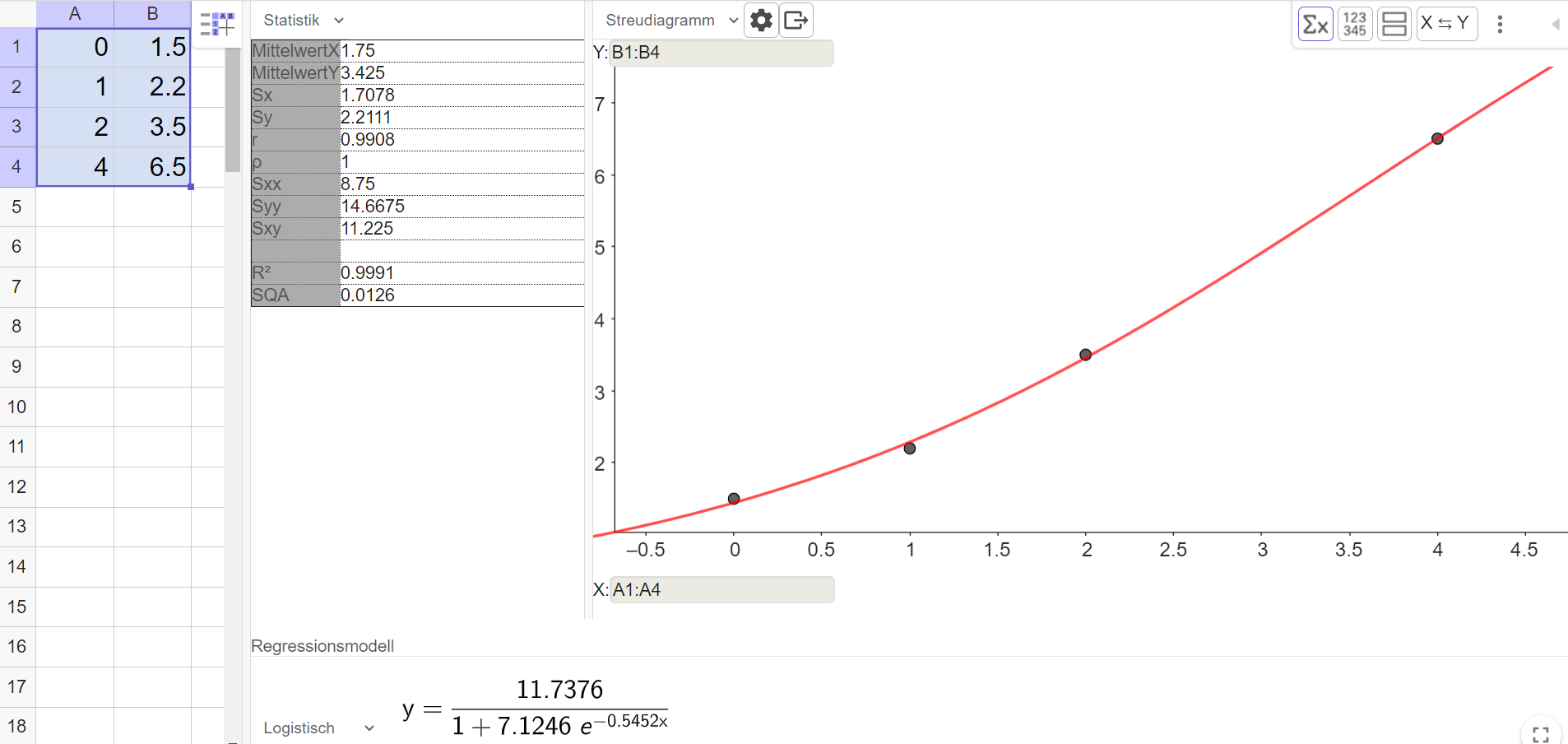
Erstelle mit dem TR oder mit Geogebra eine Regressionsfunktion mit dem Ansatz .
Herr Malinowski zeigt das Ergebnis seiner Analyse seinem Nachbarn. Der ist der Meinung, dass auch andere Regressionsfunktionen zu den Daten passen würden.
Überprüfe mit dem TR oder mit Geogebra, welche Regressionsfunktionen auch möglich sind. Was ist die beste Regressionsfunktion?
- 30
Gegeben ist die Funktion mit der Definitionsmenge
Geben Sie die Koordinaten der Schnittpunkte des Graphen von mit den Koordinatenachsen an.
Widerlegen Sie die folgende Aussage: „Die Funktion ist umkehrbar.“
Ermitteln Sie eine integralfreie Darstellung von
- 31
test
- 32
ISBN: 978-3-7430-0132-9
Buch Seite 77: Aufg. 3: Zeigen Sie, dass gilt:
Richtig: statt
Buch Seite 79: Monotonieverhalten
Wegen des negativen Vorzeichens im Zähler ist damit.....
Buch Seite 79: Steigung der Tangente , hier fehlt die 2 in der Potenz.
Buch Seite 83: Mitte: Gesucht ist die Wahrscheinlichkeit, dass die Frage nach Oberdorf und....
Buch Seite 86: Volumen der Lehmhütte: , statt der muss stehen.
Buch Seite 90: Weiterhin gilt dann: , hier muss am Ende noch das stehen. Erst in der nächsten Zeile verschwindet es.
Buch Seite 99: Hier bin ich nicht ganz sicher, ob bei der Betragsstriche braucht?
Buch Seite 112: Bei der Berechnung der Obersumme lese ich und nicht ab. Dann ist FE.
Buch Seite 113: , die 2 muss durch 3 ersetzt werden.
und 2 Zeilen weiter , hier fehlt bei der Klammer das Quadrat.
Buch Seite 114: Hier bin ich nicht ganz sicher, ob bei der Betragsstriche braucht?
Buch Seite 121: Um weiter vereinfachen zu können...... da fehlt das n bei vereinfachen.
Buch Seite 135: Bei 3. Zeile ....... , es ist etwas ungünstig, es so zu schreiben. Besser ..... zumal es in der 4. Zeile so steht.
Buch Seite 141: Oben rechts muss es heißen 2021-31.
Buch Seite 142: Oben links muss es heißen 2021-32.
Buch Seite 160: Angeben ist oben:
Das ist leider falsch. Richtig ist
Warum ist das so? Z.B. ist nach der angegebenen möglich, aber ist nicht definiert und dann darf nicht darüber integriert werden, deshalb ist .
Buch Seite 184: Widerlegen der Aussage:
(also Vorzeichen und nicht )
Buch Seite 193: Die Koordinaten des Wendepunktes sind etwas ungenau
stattdessen
Buch Seite 226: Auf der rechten Seite der Gleichung muss durch ersetzt werden.
- 33
Taschenrechnerfreier Teil
Gib an, mit welcher Wahrscheinlichkeit beide Schlüssel passen. (1 Pkt.)
Die Wahrscheinlichkeit, aus Wohnungsschlüsseln den Richtigen zu ziehen, ist .
Die Wahrscheinlichkeit, aus Briefkastenschlüsseln den Richtigen zu ziehen, ist .
.
Bestimme, mit welcher Wahrscheinlichkeit genau einer der beiden Schlüssel passt (1,5 Pkte.)
Ein Schlüssel passt nicht:
Der erste Schlüssel passt:
Der zweite Schlüssel passt:
.
Gegeben sind gleichschenklige Dreiecke mit den Basen .
Die Winkel haben das Maß mit .
Es gilt: .
Die untenstehende Zeichnung zeigt das Dreieck für .
Ergänze in der Zeichnung zu A 2.0 das Dreieck für (1 Pkt.)
In den Dreiecken gilt für den Abstand der Punkte zur Geraden : .
Kreuzen Sie das passende Intervall für an. (1 Pkt.)
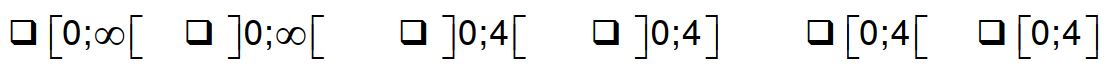

Es gilt:
Für ist dann der Abstand der Punkte zur Geraden größer null. Die linke Intervallgrenze ist ein offenes Intervall.
Für ist der Abstand der Punkte zur Geraden gleich .
Für ist der Abstand der Punkte zur Geraden kleiner als . Die rechte Intervallgrenze ist ebenfalls ein offenes Intervall.
muss angekreuzt werden.
Die Dreiecke rotieren um die Gerade .
Zeigen Sie, dass für den Oberflächeninhalt der entstehenden Rotationskörper in
Abhängigkeit von gilt: . (2,5 Pkte.)
Der Rotationskörper besteht aus zwei gleich großen Kegeln.
Für den Kegelmantel gilt: . Dabei ist die Mantellinie des Kegels und der Kegelradius ist .
Weiterhin gilt:
Durch Rotation des Dreiecks um die Gerade entsteht ein Rotationskörper mit einem Oberflächeninhalt von .
Bestimmen Sie das zugehörige Maß für . (1,5 Pkte.)
Löse die Gleichung :
↓ Löse nach auf.
A 3.0 Die Skizze zeigt das rechtwinklige Dreieck mit der Hypotenuse und dem
Schwerpunkt . Die Gerade schneidet die Seite im Punkt .
Es gilt: ; .
A 3.1 Begründen Sie ohne zu messen, dass der Punkt der Mittelpunkt der Strecke ist. (1 Pkt.)
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der drei Seitenhalbierenden. Eine Seitenhalbierende verbindet einen Eckpunkt mit dem Mittelpunkt der gegenüberliegenden Seite. Hier ist der Punkt der Schwerpunkt des Dreiecks . Deshalb ist die Strecke eine Seitenhalbierendeder Punkt ist der Mittelpunkt der Strecke .
A 3.2 Bestimmen Sie mithilfe einer Rechnung das Maß des Winkels . (2 Pkte.)
Es gilt:
Das Maß des Winkels beträgt .
Taschenrechner Teil
B 1.0 Fünftklässler bemalen für die Abschlussprüflinge ihrer Schule kleine Schachteln mit roter („r“), blauer („b“), grüner („g“) oder weißer („w“) Farbe und befüllen jede Schachtel mit einer Süßigkeit. Für die Befüllung stehen Süßigkeiten in den drei Geschmacksrichtungen Apfel („A“), Birne („B“) oder Mango („M“) zur Verfügung.
Das Baumdiagramm zeigt entsprechende Anteile. Es gilt: .
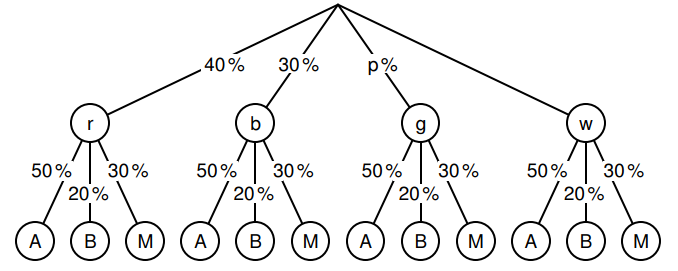
B 1.1 Kreuzen Sie den Anteil der weißen Schachteln an. (1 Pkt.)

, kreuze entsprechend an.
B 1.2 Vor dem Prüfungsraum gibt eine Lehrkraft jedem Prüfling eine zufällig ausgewählte Schachtel. Die Wahrscheinlichkeit dafür, dass die erste ausgegebene Schachtel grün ist und eine Süßigkeit in der Geschmacksrichtung Apfel enthält, beträgt .
Berechnen Sie den Anteil der grünen Schachteln. (1,5 Pkte.)
Es gilt:
Der Anteil der grünen Schachteln beträgt .
B 1.3 Sebastian wünscht sich eine rote oder eine blaue Schachtel mit einer Süßigkeit, die nicht die Geschmacksrichtung Birne hat. Er vermutet, dass die erste ausgegebene Schachtel mit einer Wahrscheinlichkeit von mehr als seinem Wunsch entspricht.
Beurteilen Sie diese Vermutung. (2,5 Pkte.)
Nicht die Geschmacksrichtung Birne Apfel oder Mango
Rote Schachtel, blaue Schachtel.
Damit gilt:
Wegen trifft Sebastians Vermutung zu.
- 34
Gegeben ist die Funktion .
Geben Sie die maximale Definitionsmenge von , die jeweilige Art der Definitionslücken von , die Nullstellen von , sowie die Art und die Gleichung aller Asymptoten von an.
In der Abbildung ist der Graph dargestellt.
Entscheiden Sie durch Ankreuzen, ob folgende Terme Werte haben, die größer null, kleiner null oder gleich null sind.
Gegeben sind die Funktionen und .
Bestimmen Sie die maximale Definitionsmenge der beiden Funktionen.
Lösen Sie die beiden folgenden Gleichungen über der Grundmenge der rationalen Zahlen:
i)
ii)
Skateboardrampe:
Der Flächeninhalt der Skateboardrampe beträgt .
i) Gegeben ist ein rechteckiges Solarmodul mit und . Bestimmen Sie die Koordinaten des Eckpunktes .
ii) Bestimmen Sie nachvollziehbar eine Gleichung der Ebene in der das Solarmodul liegt, in Parameterform.
Berechnen Sie die Maßzahl des Flächeninhalts des Solarmoduls.
Gegeben sind die Koordinaten der Punkte und .
Zeigen Sie, dass die Strebe senkrecht auf der Ebene steht.
- 35
Lösen Sie die beiden folgenden Gleichungen über der Grundmenge der reellen Zahlen. [4 BE]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?