Untersuche $f$ rechnerisch auf lokale Extremstellen

Die notwendige Bedingung für ein Extremum ist $f^{\prime }(x)=0$.

Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung:

$f^{\prime }(x)=10\cdot (1\cdot e^{-x}+(x-1)\cdot e^{-x}\cdot (-1))=10\cdot (2-x)\cdot e^{-x}$

$f^{\prime }(x)=0\Rightarrow 0=10\cdot (2-x)\cdot e^{-x}$

Weil ${\mathrm{e}}^{-x}\ne 0$ für alle $x\in ℝ$ folgt mit dem Satz vom Nullprodukt:

$2-x=0\Rightarrow x=2$

Die hinreichende Bedingung für ein Extremum ist $f^{\prime \prime }(x)\ne 0$.

Bilde mithilfe der Produkt- und Kettenregel die 2. Ableitung:

$f^{\prime \prime }(x)=10\cdot ((-1)\cdot e^{-x}+(2-x)\cdot e^{-x}\cdot (-1))=10\cdot (x-3)\cdot e^{-x}$

$f^{\prime \prime }(2)=10\cdot (2-3)\cdot e^{-2}=-10\cdot e^{-2}<0$

Die Funktion $f$ hat genau eine lokale Extremstelle.

Der Graph von $f$ hat bei $x=2$ ein lokales Maximum.

Zeige rechnerisch, dass der Punkt $(12|2160)$ ein Hochpunkt des Graphen von $f$ ist

Gegeben ist $f(x)=-\frac{5}{16}{x}^4+5x^3$.

Berechne $f^{\prime }(x)$ und $f^{\prime \prime }(x)$:

$f^{\prime }(x)=-\frac{5}{4}{x}^3+15x^2$

$f^{\prime \prime }(x)=-\frac{15}{4}{x}^2+30x$

Die notwendige Bedingung für ein Extremum ist $f^{\prime }(x)=0$.

$\Rightarrow 0=-\frac{5}{4}{x}^3+15x^2=5x^2\cdot (-{\displaystyle \frac{1}{4}}x+3)$

Mit dem Satz vom Nullprodukt folgt:

$x=0\vee -{\displaystyle \frac{1}{4}}x+3=0\Rightarrow x=12$

Lokale Extremstellen sind also $x=0$ oder $x=12$.

Nach Aufgabenstellung muss nur $x=12$ beachtet werden.

Die hinreichende Bedingung für ein Extremum ist $f^{\prime \prime }(x)\ne 0$.

$\Rightarrow f^{\prime \prime }(12)=-\frac{15}{4}\cdot {12}^2+30\cdot 12=-180<0\Rightarrow$ Maximum

Berechne $f(12)=-\frac{5}{16}\cdot {12}^4+5\cdot {12}^3=2160$.

Der Punkt $(12|2160)$ ist ein Hochpunkt des Graphen von $f$.

Zeige rechnerisch, dass die Tangente an den Graphen von $f$ im Punkt $(0|0)$ parallel zur $x$-Achse verläuft

Es ist $f^{\prime }(0)=0$ und $f(0)=0$.

Im Punkt $(0|0)$ verläuft die Tangente an den Graphen von $f$ parallel zur $x$-Achse.

Bestimme eine Gleichung der Geraden $g$, die durch die beiden Wendepunkte des Graphen von $f$ verläuft

Berechne die Wendepunkte:

Die notwendige Bedingung für einen Wendepunkt ist $f^{\prime \prime }(x)=0$.

$\Rightarrow 0=-\frac{15}{4}{x}^2+30x=15\cdot x(-{\displaystyle \frac{1}{4}}\cdot x+2)$

Mit dem Satz vom Nullprodukt folgt:

$x=0\vee -{\displaystyle \frac{1}{4}}x+2=0\Rightarrow x=8$

Wendestellen liegen bei $x=0$ oder $x=8$ vor, wenn die hinreichende Bedingung $f^{\prime \prime \prime }(x)\ne 0$ erfüllt ist.

Berechne $f^{\prime \prime \prime }(x)=-\frac{15}{2}x+30\Rightarrow f^{\prime \prime }(0)=30\ne 0$ und $f^{\prime \prime \prime }(8)=-\frac{15}{2}\cdot 8+30=-30\ne 0$

Die Bedingung ist erfüllt, d.h. Wendestellen liegen bei $x=0$ oder $x=8$ vor.

Berechne $f(0)=0$ und $f(8)=-\frac{5}{16}\cdot 8^4+5\cdot 8^3=1280$.

Die Wendepunkte haben die Koordinaten $W{P}_1(0|0)$ und $W{P}_2(8|1280)$.

Für die Geradengleichung $g$ benutze die Zwei-Punkte-Form der Geradengleichung:

$y={\displaystyle \frac{y_2-y_1}{x_2-x_1}}\cdot (x-x_1)+y_1\Rightarrow y={\displaystyle \frac{1280-0}{8-0}}\cdot (x-0)+0$

$\Rightarrow g:y=160\cdot x$

Die Gleichung der Geraden $g$, die durch die beiden Wendepunkte des Graphen von $f$ verläuft, lautet $y=160\cdot x$.

Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0\le x\le 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat

Berechne alle Schnittpunkte des Graphen $G_f$ mit den Koordinatenachsen

Gegeben ist $f(x)={\displaystyle \frac{1}{10}}(-x^3+15x^2-56x+12)$.

Schnittpunkte mit der x-Achse:

$f(x)=0\Rightarrow {\displaystyle \frac{1}{10}}(-x^3+15x^2-56x+12)=0\Rightarrow -x^3+15x^2-56x+12=0$

Die Nullstelle der Funktion $g(x)=-x^3+15x^2-56x+12$ ist bekannt $x_N=6$.

Führe eine Polynomdivision durch.

$\begin{array}{l}\phantom{-}(-x^3+15x^2-56x+12):(x-6)=-x^2+9x-2\\ -\underline{(-x^3+6x^2)}\\ \phantom{-(x^3-1}9x^2-56x\\ \phantom{(x^3+}-\underline{(9x^2-54x)}\\ \phantom{-(x^3+3x^2-}-2x+12\\ \phantom{(x3+3x^2-}-\underline{(-2x+12)}\\ \phantom{-(x^3+3x^2-4x-12}0\end{array}$

Löse nun die Gleichung $-x^2+9x-2=0\Rightarrow x^2-9x+2=0$ mit der pq-Formel:

Somit lauten die Schnittpunkte von $G_f$ mit der x-Achse $N_1(6|0),N_2(\mathrm{4,5}-\sqrt{\mathrm{18,25}}|0)\approx$$N_2(\mathrm{0,23}|0)$ und $N_3(\mathrm{4,5}+\sqrt{\mathrm{18,25}}|0)\approx N_3(\mathrm{8,77}|0)$.

Schnittpunkt mit der y-Achse:

Setze $x=0$ in $f(x)$ ein $\Rightarrow f(0)=12\Rightarrow S_y(0|12)$.

Der Schnittpunkt mit der y-Achse ist $S_y(0|12)$.

Ermittle Art und Koordinaten aller relativen Extrempunkte von $G_f$

Aufg. 1 Teil 1: ohne Hilfsmittel – Analysis

Gegeben ist die Funktion $f:x\mapsto {\displaystyle \frac{2x}{4-x^2}}$ mit der Definitionsmenge $D_f=]-2;2[$.

Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.

a) Geben Sie die Gleichungen aller Asymptoten von $G_f$ und die Nullstelle von $f$ an.

(2 BE)

b) Weisen Sie nach, dass die Funktion $f$ in ihrer Definitionsmenge $D_f$ umkehrbar ist, und ermitteln Sie die Definitionsmenge der Umkehrfunktion von $f$. (6 BE)

c) Der Graph von $f$ und die zur x-Achse senkrechte Gerade bei $x=1$ schließen zusammen mit der x-Achse im I. Quadranten ein Flächenstück ein.

Berechnen Sie die exakte Maßzahl des Flächeninhalts dieses Flächenstücks. (4 BE)

d) Gegeben ist nun die Funktion $g:x\mapsto \ln (f(x))$ mit der maximalen Definitionsmenge $D_g\subset D_f$. Ermitteln Sie die Definitionsmenge $D_g$ und die exakte Nullstelle von $g$. (5 BE)

Aufg. 2 Teil 1: ohne Hilfsmittel – Analysis

Die nachfolgende Abbildung zeigt einen Ausschnitt des Graphen $G_h$ einer in $ℝ$ stetigen Funktion $h$. Die x-Achse ist Asymptote $von{G}_h$. Außerdem gilt: $h(x)\ge 0$ für $x\in ℝ$.

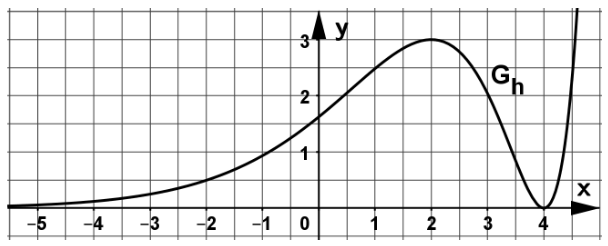
Zudem ist die Funktion $$H:x\mapsto {\displaystyle {\int }_2^{x}h(t)\mathrm{d}t}$$ mit der Definitionsmenge $D_H=ℝ$ gegeben.

Entscheiden Sie für die beiden folgenden Aussagen jeweils, ob die Aussage wahr oder falsch ist, und begründen Sie Ihre Entscheidung.

A: „Der Graph von $H$ besitzt bei $x=4$ einen Extrempunkt.“

B: „Der Graph von $H$ hat bei $x=1$ eine Tangente mit einem positiven y-Achsenabschnitt.“

(5 BE)

Teil 2: mit Hilfsmitteln – Analysis I

1 Gegeben ist die Funktion $f:x\mapsto \arctan (1-{\displaystyle \frac{2}{5x}})$ mit der Definitionsmenge$D_f=ℝ\backslash \{0\}$.

Der Graph von $f$ in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.

a) Berechnen Sie die Nullstelle von $f$. Bestimmen Sie außerdem das Verhalten der

Funktionswerte von $f$ an den Rändern der Definitionsmenge und geben Sie die Gleichung der Asymptote von $G_f$ an. (7 BE)

b) Ermitteln Sie das Steigungsverhalten von $G_f$ und geben Sie die Wertemenge von $f$ an. $[\text{Mögliches Teilergebnis}:f^{\prime }(x)={\displaystyle \frac{1}{5x^2-2x+\mathrm{0,4}}}]$ (5 BE)

c) Bestimmen Sie die Koordinaten des Wendepunkts von $G_f$.

Teil 2: mit Hilfsmitteln – Analysis I

2 Gegeben ist die Funktion $u:x\mapsto {\displaystyle \frac{2\ln (x)}{\ln (x)-1}}$ mit der Definitionsmenge $D_u=]\text{e};+\infty [$.

a) Zeigen Sie, dass der Graph der Funktion u streng monoton fallend ist. (4 BE)

b) Die Funktion $u$ ist umkehrbar (Nachweis nicht erforderlich). Ermitteln Sie einen Term der Umkehrfunktion von $u$. (3 BE)

Teil 2: mit Hilfsmitteln – Analysis I

3 Gegeben sind die Funktionen $h(x)={\displaystyle \frac{12x^2-14x}{(2x-3)\cdot (3x+1)}}$ und $$H:x\mapsto {\displaystyle {\int }_0^{x}h(t)\mathrm{d}t}$$ mit den jeweils maximalen Definitionsmengen $D_h\subset ℝ$ und $D_H\subset ℝ$.

a) Bestimmen Sie die maximale Definitionsmenge von $H$, sowie jeweils Art und

x-Koordinaten aller Extrempunkte des Graphen von $H$. (7 BE)

b) Zeigen Sie, dass $h(x)$ auch in der Form ${\displaystyle \frac{6}{(2x-3)\cdot (3x+1)}}+2$ dargestellt werden kann. Ermitteln Sie anschließend eine integralfreie Darstellung von $H$. (8 BE)

Teil 2: mit Hilfsmitteln – Analysis I

4 Weinkenner sind davon überzeugt, dass je nach Weinsorte die passende Weintemperatur wichtig für den Genuss des Weins ist. So soll zum Beispiel Rotwein bei Raumtemperatur genossen werden. Mit einem Wein-Thermometer wird in einem Raum die Temperatur des Weins gemessen, die niedriger als die Raumtemperatur ist. In dieser Aufgabe zeigt das Wein-Thermometer unmittelbar vor dem Eintauchen in den Wein die Raumtemperatur von ${20}^{\circ }C$ an. Nach dem Eintauchen in den Wein wird es erst allmählich die Weintemperatur $T_W$ anzeigen. Sowohl die Raumtemperatur als auch die Weintemperatur sind während der Messung als konstant zu betrachten.

Die vom Wein-Thermometer in der Einheit ${}^{\circ }C$ angezeigte Temperatur $T(t)$ in Abhängigkeit von der Zeit $t$ (gemessen in Sekunden ab dem Zeitpunkt $t=0$ des Eintauchens) lässt sich durch die Differenzialgleichung $\dot{T}=-\lambda \cdot (T-T_W)$ beschreiben, wobei $\lambda >0$ ein reeller Parameter ist. Auf das Mitführen der Einheiten wird im Folgenden verzichtet.

Zeigen Sie, dass die Funktion $T_D:t\mapsto D\cdot e^{-\lambda \cdot t}$ für jeden Wert von $D\in ℝ$ eine Lösung der obigen Differenzialgleichung ist, und begründen Sie, warum in der vorliegenden Situation $D=20-T_W$ gelten muss. (4 BE)

Teil 2: mit Hilfsmitteln – Analysis II

1 Gegeben ist die Funktion $f:x\mapsto \ln (4-{\displaystyle \frac{8x}{x^2+1}})$ mit der maximalen Definitionsmenge $D_f\subset ℝ$.

Der Graph von $f$ in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.

a) Zeigen Sie, dass $D_f=ℝ\backslash \{1\}$ ist, und berechnen Sie die Nullstellen von $f$ auf eine

Nachkommastelle genau. (6 BE)

b) Ermitteln Sie die Gleichungen aller Asymptoten von $G_f$. (5 BE)

c) Ermitteln Sie die maximalen Monotonieintervalle von $G_f$ und bestimmen Sie damit Art und Koordinaten des Extrempunkts von $G_f$.

$[\text{Mögliches Teilergebnis}:f^{\prime }(x)={\displaystyle \frac{2\cdot (x+1)}{(x-1)\cdot (x^2+1)}}]$ (8 BE)

Teil 2: mit Hilfsmitteln – Analysis II

2 Nun wird die Funktion $$h:x\mapsto {\displaystyle {\int }_{\mathrm{0,6}}^x{\displaystyle \frac{3}{(5t-1{)}^2+4}}\mathrm{d}t}$$ mit der Definitionsmenge $D_h=ℝ$ betrachtet.

a) Ermitteln Sie ohne Verwendung einer integralfreien Darstellung von $h$ die Anzahl und die Lage der Nullstellen von $h$. (3 BE)

b) Ermitteln Sie eine integralfreie Darstellung von h. (6 BE)

Teil 2: mit Hilfsmitteln – Analysis II

3.0 Gegeben ist die Funktion $g:x\mapsto {\displaystyle \frac{2}{2e^{-x}+1}}-1$ mit der Definitionsmenge $D_g=[0;+\infty [$. Der Graph von $g$ in einem kartesischen Koordinatensystem wird mit $G_g$ bezeichnet.

a) Begründen Sie für die folgenden Aussagen jeweils, ob sie wahr oder falsch sind.

A: „Der Graph von $g$ hat bei $x=0$ einen absoluten Extrempunkt.“

B: „Die Gerade mit der Gleichung $y=1$ ist Asymptote von $G_g$.“

$[\text{Mögliches Teilergebnis}:g^{\prime }(x)={\displaystyle \frac{4e^{-x}}{{(2e^{-x}+1)}^2}}]$ (6 BE)

b) Die Funktion $g$ ist umkehrbar (Nachweis ist nicht erforderlich). Die Tangente $t$ berührt den Graphen der Umkehrfunktion von $g$ im Punkt $P^{\ast }(\frac{1}{2}|?)$. Ermitteln Sie die Steigung der Tangente $t$. (5 BE)

Teil 2: mit Hilfsmitteln – Analysis II

4 Auf einen bestimmten Körper wirkt zu jedem Zeitpunkt $t\ge 0$ seit Beobachtungsbeginn $(t=0)$ eine konstante Kraft. Außerdem wirkt auf den Körper eine Reibungskraft, die proportional zum Quadrat der Momentangeschwindigkeit $v(t)$ des Körpers ist. Es gilt modellhaft die Differenzialgleichung $5\dot{v}=50-2v^2$. Die Geschwindigkeit wird in ${\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}$, die Zeit in $\mathrm{s}$ angegeben. Bei den folgenden Berechnungen darf auf das Mitführen der Einheiten verzichtet werden.

Untersuchen Sie, ob die Funktion v mit der Gleichung $v(t)=5\cdot {\displaystyle \frac{e^{4t}-1}{e^{4t}+1}}$ eine spezielle

Lösung der Differenzialgleichung ist. (4 BE)

Abitur Bayern 2025 Analysis m.H.

Gegeben ist die Funktion $f:x\mapsto {\displaystyle \frac{-x^2-5}{x^3-5x}}$ mit ihrer Definitionsmenge $D_f=ℝ\backslash \{-\sqrt{5};0;\sqrt{5}\}.$

Der Graph der Funktion wird mit $G_f$ bezeichnet.

a) Untersuchen Sie, ob $G_f$ eine Symmetrie zum Koordinatensystem besitzt. (3 BE)

b) Ermitteln Sie die exakten Nullstellen der ersten Ableitungsfunktion $f^{\prime }$ mit der Definitionsmenge $D_{f^{\prime }}=D_f$.

c) Die nachfolgende Abbildung zeigt einen Ausschnitt des Graphens von $D_{f^{\prime }}$ der Funktion $f^{\prime }$. Alle Nullstellen und Definitionslücken sind in der Abbildung ersichtlich. Geben Sie die maximalen Monotonieintervalle sowie jeweils die Art aller Extremstellen von $f$ an.

Hinweis: Anstelle der exakten Zahlenwerte können bei der Angabe der Intervalle die in der Abbildung ersichtlichen Bezeichnungen $x_1,x_2,x_3$ und $x_4$ verwendet werden.

d) Zeigen Sie, dass die Funktion $f:x\mapsto {\displaystyle \frac{-x^2-5}{x^3-5x}}$ auch durch die Gleichung $f(x)={\displaystyle \frac{1}{x}}-{\displaystyle \frac{2x}{x^2-5}}$ dargestellt werden kann und berechnen Sie das bestimmte Integral $${\displaystyle {\int }_1^{2}f(x)\mathrm{d}x}$$. (7 BE)

2. Bei der Milchsäuregärung wandeln Bakterien die in der Milch befindliche Laktose in Milchsäure um. Die Funktion $M:t\mapsto {\displaystyle \frac{a}{1+9\cdot e^{bt}}}$ mit $a,b,t\in ℝ$ und $t\ge 0$ gibt die Milchsäurekonzentration $M(t)$ in Abhängigkeit von der Zeit $t$ an. Dabei wird $M(t)$ in Gramm pro Liter $\left({\displaystyle \frac{\mathrm{g}}{\mathrm{l}}}\right)$ gemessen und $t$ gibt die Zeit in Stunden an, die seit Beobachtungsbeginn vergangen ist. Bei Rechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf eine Nachkommastelle.

a) In einem Laborversuch wird die Milchsäurekonzentration von einem Liter Milch stündlich gemessen. Zu Beobachtungsbeginn $(t=0)$ beträgt die Milchsäurekonzentration $\mathrm{0,8}$ Gramm pro Liter und $3$ Stunden nach Beobachtungsbeginn $\mathrm{5,0}$ Gramm pro Liter. Berechnen Sie die Werte der Parameter $a$ und $b$ so, dass die Modellfunktion mit diesen beiden Messwerten in Einklang steht. (3 BE)

b) Im Folgenden gilt $a=8$ und $b=-\mathrm{0,9}$. Somit ergibt sich $M(t)={\displaystyle \frac{8}{1+9\cdot e^{-\mathrm{0,9}t}}}$ mit $t\ge 0$. Der Graph von $M$ wird mit $G_M$ bezeichnet.

1. Zeigen Sie, dass die Milchsäurekonzentration nach diesem Modell stetig zunimmt.

[ Mögliches Teilergebnis $\dot{M}(t)={\displaystyle \frac{\mathrm{64,8}\cdot e^{-\mathrm{0,9}t}}{(1+9\cdot e^{-\mathrm{0,9}t}{)}^2}}$] (4 BE)

2. Für die zweite Ableitungsfunktion $\ddot{M}$ gilt $\ddot{M}(t)=-\mathrm{58,32}\cdot e^{-\mathrm{0,9}t}\cdot {\displaystyle \frac{1-9\cdot e^{-\mathrm{0,9}t}}{(1+9\cdot e^{-\mathrm{0,9}t}{)}^3}}$ mit $t>0$. (Nachweis nicht erforderlich.)

Ermitteln Sie den Zeitpunkt $t_1$, zu dem die erste Ableitungsfunktion $\dot{M}$ ein absolutes Maximum besitzt. Berechnen Sie die Differenz $M(t_1+\mathrm{0,5})-M(t_1-\mathrm{0,5})$ und interpretieren Sie diesen Wert im Sachzusammenhang. (6 BE)

3. Zeichne Sie $G_M$ im Bereich $0\le t\le 13$ in ein Koordinatensystem. Wählen Sie auf beiden Achsen einen geeigneten Maßstab. Kennzeichnen Sie auch die Differenz $M(t_1+\mathrm{0,5})-M(t_1-\mathrm{0,5})$ in Ihrer Abbildung. (4 BE)

4. Weisen Sie nach, dass die Funktion $G:t\mapsto {\displaystyle \frac{80}{9}}\cdot \ln (9+e^{\mathrm{0,9}t})$ mit der Definitionsmenge $D_G=[0;+\infty [$ eine Stammfunktion von $M$ ist. (3 BE)

5. Die durchschnittliche Milchsäurekonzentration $\overline{M}$ in ${\displaystyle \frac{\mathrm{g}}{\mathrm{l}}}$ über einen Zeitraum $[t_{1\ast };t_2]$ in Stunden beträgt $$\overline{M}={\displaystyle \frac{1}{t_2-t_1}}{\displaystyle {\int }_{t_{1\ast }}^{t_2}M(t)\mathrm{d}t}$$.

Berechnen Sie die Milchsäurekonzentration in dieser Milchprobe in den ersten sechs Beobachtungsstunden. (3 BE)

$($aus $4.:G:t\mapsto {\displaystyle \frac{80}{9}}\cdot \ln (9+e^{\mathrm{0,9}t})$$)$

Analytische Geometrie

1 In einem kartesischen Koordinatensystem sind die Punkte $A(12|2|5)$, $B(10|8|3),C(2|6|9)$ und $D(4|2|0)$ gegeben.

Runden Sie Ihre Endergebnisse gegebenenfalls auf eine Nachkommastelle.

a) Bestimmen Sie die Lösungsmenge der Gleichung $r\cdot \overrightarrow{AB}+s\cdot \overrightarrow{AC}+t\cdot \overrightarrow{AD}=0$ mit $r,s,t\in ℝ$ und interpretieren Sie Ihr Ergebnis geometrisch. (6 BE)

b) Berechnen Sie die Maßzahl des Flächeninhaltes des Dreiecks $BCD$. (3 BE)

c) Die Gerade $g_{AB}$ verläuft durch die Punkte $A$ und $B$.

Es gilt: $C\notin g_{AB}$. (Nachweis nicht erforderlich!)

Berechnen Sie den Abstand der Geraden $g_{AB}$ zum Punkt $C$. (5 BE)

2

Zu FOS 2022 Aufg.2 Alternative

Nach Aufgabe b) gilt: Der Nenner $N(x)$ der 1. Ableitung ist die Gleichung einer nach oben geöffneten Parabel mit Scheitelpunkt $S(\mathrm{0,2}|\mathrm{0,2})$.

Da $f^{\prime }(x)={\displaystyle \frac{1}{N(x)}}$ ist, hat die 1. Ableitung bei $x=\mathrm{0,2}$ einen Hochpunkt $\Rightarrow$ bei $x=\mathrm{0,2}$ ist dann $f^{\prime \prime }(\mathrm{0,2})=0\Rightarrow$Wendepunkt.

$f(\mathrm{0,2})=\arctan (1-{\displaystyle \frac{2}{5\cdot \mathrm{0,2}}})=\arctan (1-2)=\arctan (-1)=-{\displaystyle \frac{\pi }{4}}\Rightarrow WP(\mathrm{0,2}|-\frac{\pi }{4})$

Die Koordinaten des Wendepunkts von $G_f$ sind $WP(\mathrm{0,2}|-\frac{\pi }{4})$.