Aufgaben - lernen mit Serlo!

Testlösungen Abitur BW

Aufgabe 6.1

$\begin{array}{rccccccc} I & x_{1} & + & x_{2} & + & 7 x_{3} & = & 2 \\ II & 2 x_{1} & - & x_{2} & - & 3 x_{3} & = & - 5 \\ III & 4 x_{1} & - & x_{2} & + & 4 x_{3} & = & - 7 \end{array} $

Zunächst solltest du es zu einer erweiterten Koeffizientenmatrix umschreiben:

$(\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 2 & - 1 & - 3 & - 5 \\ 4 & - 1 & 4 & - 7 \end{array})$

Als ersten Schritt des Gaußverfahrens verwendest du jetzt das Additionsverfahren, um die beiden Einträge, die jetzt $orange$ markiert sind auf null zu bringen.

$\begin{array}{c} (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 2 & - 1 & - 3 & - 5 \\ 4 & - 1 & 4 & - 7 \end{array}) & \underset{\to}{II - 2 \cdot I} & (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 4 & - 1 & 4 & - 7 \end{array}) \\ (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 4 & - 1 & 4 & - 7 \end{array}) & \underset{\to}{III - 4 \cdot I} & (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & - 5 & - 24 & - 15 \end{array}) \end{array}$

Dazu ziehst du von der zweiten Zeile das Doppelte der ersten Zeile ab $(II - 2 \cdot I)$ .

Anschließend ziehst du von der dritten Zeile das Vierfache der ersten Zeile ab $(III - 4 \cdot I)$ .

Jetzt gibt es in deiner erweiterten Koeffizientenmatrix nur noch einen Eintrag unter der Diagonalen, der nicht null ist, in der Matrix ist er $grün$ markiert.

Damit auch in diesem Eintrag der Matrix eine null steht, addierst du nun zum minus Dreifachen der dritten Zeile das Fünffache der zweiten Zeile $(- 3 \cdot III + 5 \cdot II)$ .

$\begin{array}{c} (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & - 5 & - 24 & - 15 \end{array}) & \underset{\to}{- 3 \cdot III + 5 \cdot II} & (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & 0 & - 13 & 0 \end{array}) \end{array}$

Die letzte Zeile lautet nun: $- 13 x_{3} = 0 \Rightarrow x_{3} = 0$

Aus Zeile $2$ folgt dann mit $x_{3} = 0$ : $- 3 x_{2} - 17 \cdot 0 = - 9 \Rightarrow x_{2} = 3$

Aus Zeile $1$ folgt dann mit $x_{3} = 0$ und $x_{2} = 3$ : $x_{1} + 3 - 7 \cdot 0 = 2 \Rightarrow x_{1} = - 1$

Antwort: Das lineare Gleichungssystem hat die Lösungsmenge $𝕃 = {(- 1 | 3 | 0}$

Aufgabe 6.2

Du machst den Ansatz: $\vec{v} = r \cdot \vec{a} + s \cdot \vec{b} + t \cdot \vec{c}$

$(\begin{array}{c} 14 \\ - 5 \\ 7 \end{array}) = r \cdot (\begin{array}{c} 0 \\ 1 \\ 3 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 3 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 5 \\ - 2 \\ 2 \end{array})$

Um das Gaußverfahren anzuwenden, sollte in der erweiterten Koeffizientenmatrix an der ersten Stelle keine $0$ stehen. Deshalb werden die Spalten $1$ und $2$ vertauscht.

$(\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 3 & 1 & - 2 & - 5 \\ 7 & 3 & 2 & 7 \end{array})$

Als ersten Schritt des Gaußverfahrens verwendest du jetzt das Additionsverfahren, um die beiden Einträge, die jetzt $orange$ markiert sind auf null zu bringen.

$\begin{array}{c} (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 3 & 1 & - 2 & - 5 \\ 7 & 3 & 2 & 7 \end{array}) & \underset{\to}{II + 3 \cdot I} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 7 & 3 & 2 & 7 \end{array}) \\ (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 7 & 3 & 2 & 7 \end{array}) & \underset{\to}{III + 7 \cdot I} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 3 & 37 & 105 \end{array}) \end{array}$

Dazu addierst du zur zweiten Zeile das Dreifache der ersten Zeile $(II + 3 \cdot I)$ .

Anschließend addierst du zur dritten Zeile das Siebenfache der ersten Zeile $(III + 7 \cdot I)$ .

Jetzt gibt es in deiner erweiterten Koeffizientenmatrix nur noch einen Eintrag unter der Diagonalen, der nicht null ist, in der Matrix ist er $grün$ markiert.

Damit auch in diesem Eintrag der Matrix eine null steht, subtrahierst du das Dreifache der zweiten Zeile von der dritten Zeile $(III - 3 \cdot II)$ .

$\begin{array}{c} (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 3 & 37 & 105 \end{array}) & \underset{\to}{III - 3 \cdot II} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 0 & - 2 & - 6 \end{array}) \end{array}$

Die letzte Zeile lautet nun: $- 2 \cdot t = - 6 \Rightarrow t = 3$

Aus Zeile $2$ folgt dann mit $t = 3$ : $r + 13 \cdot 3 = 37 \Rightarrow r = - 2$

Aus Zeile $1$ folgt dann mit $t = 3$ und $r = - 2$ : $- s + 0 \cdot (- 2) + 5 \cdot 3 = 14 \Rightarrow s = 1$

Antwort: Der Vektor $\vec{v}$ kann durch die folgende Linearkombination dargestellt werden:

$(\begin{array}{c} 14 \\ - 5 \\ 7 \end{array}) = (- 2) \cdot (\begin{array}{c} 0 \\ 1 \\ 3 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 3 \\ 7 \end{array}) + 3 \cdot (\begin{array}{c} 5 \\ - 2 \\ 2 \end{array})$

Aufgabe 6.3

Lösung zu a)

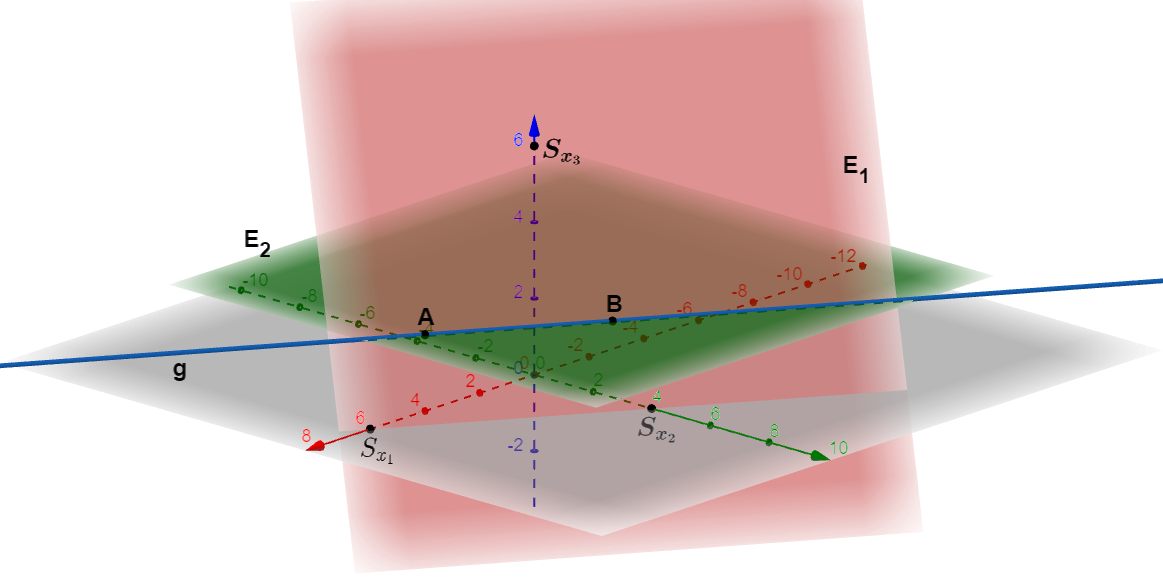
Die rote Ebene ist die Ebene $E_{1}$ in Koordinatenform: $2 x_{1} + 3 x_{2} + 2 x_{3} = 12$

In Achsenabschnittsform lautet $E_{1}$ : $\frac{x_{1}}{6} + \frac{x_{2}}{4} + \frac{x_{3}}{6} = 1$

So können die Achsenschnittpunkte (Spurpunkte) abgelesen werden: $S_{x_{1}} (6 | 0 | 0)$ ; $S_{x_{2}} (0 | 4 | 0)$ ; $S_{x_{3}} (0 | 0 | 6)$

Die grüne Ebene ist die Ebene $E_{2}$ : $x_{3} = 2$ . Sie hat den Achsenschnittpunkt $S_{x_{3}} (0 | 0 | 2)$ und sie liegt parallel zur $x_{1}$ - $x_{2}$ -Ebene.

Lösung zu b)

Du suchst zwei Punkte, die in beiden Ebenen liegen.

Für alle Werte von $x_{1}$ liegt der Punkt $A (x_{1} | 0 | 2)$ in der Ebene $E_{2}$ ( $A$ erfüllt die Ebenengleichung).

Für alle Werte von $x_{2}$ liegt der Punkt $B (0 | x_{2} | 2)$ in der Ebene $E_{2}$ ( $B$ erfüllt die Ebenengleichung).

Die Punkte $A$ und $B$ sollen gemeinsame Punkte der beiden Ebenen sein. Deshalb müssen beide Punkte auch die Ebenengleichung $E_{1}$ erfüllen.

$A \in E_{1} \Rightarrow 2 \cdot x_{1} + 3 \cdot 0 + 2 \cdot 2 = 12 \Rightarrow x_{1} = 4 \Rightarrow A (4 | 0 | 2)$

$B \in E_{1} \Rightarrow 2 \cdot 0 + 3 \cdot x_{2} + 2 \cdot 2 = 12 \Rightarrow x_{2} = \frac{8}{3} \Rightarrow B (0 | \frac{8}{3} | 2)$

Die Schnittgerade ergibt sich dann zu: $g : \vec{X} = \vec{O A} + r \cdot \vec{A B}$

$g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot ((\begin{array}{c} 0 \\ \frac{8}{3} \\ 2 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 2 \end{array})) = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ \frac{8}{3} \\ 0 \end{array})$

Der Richtungsvektor kann noch vereinfacht werden: $(\begin{array}{c} - 4 \\ \frac{8}{3} \\ 0 \end{array}) \underset{\to}{\cdot 3} (\begin{array}{c} - 12 \\ 8 \\ 0 \end{array}) \underset{\to}{: 4} (\begin{array}{c} - 3 \\ 2 \\ 0 \end{array})$

Antwort: Die Gleichung der Schnittgeraden lautet: $g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 3 \\ 2 \\ 0 \end{array})$

Aufgabe 6.4

Lösung zu a)

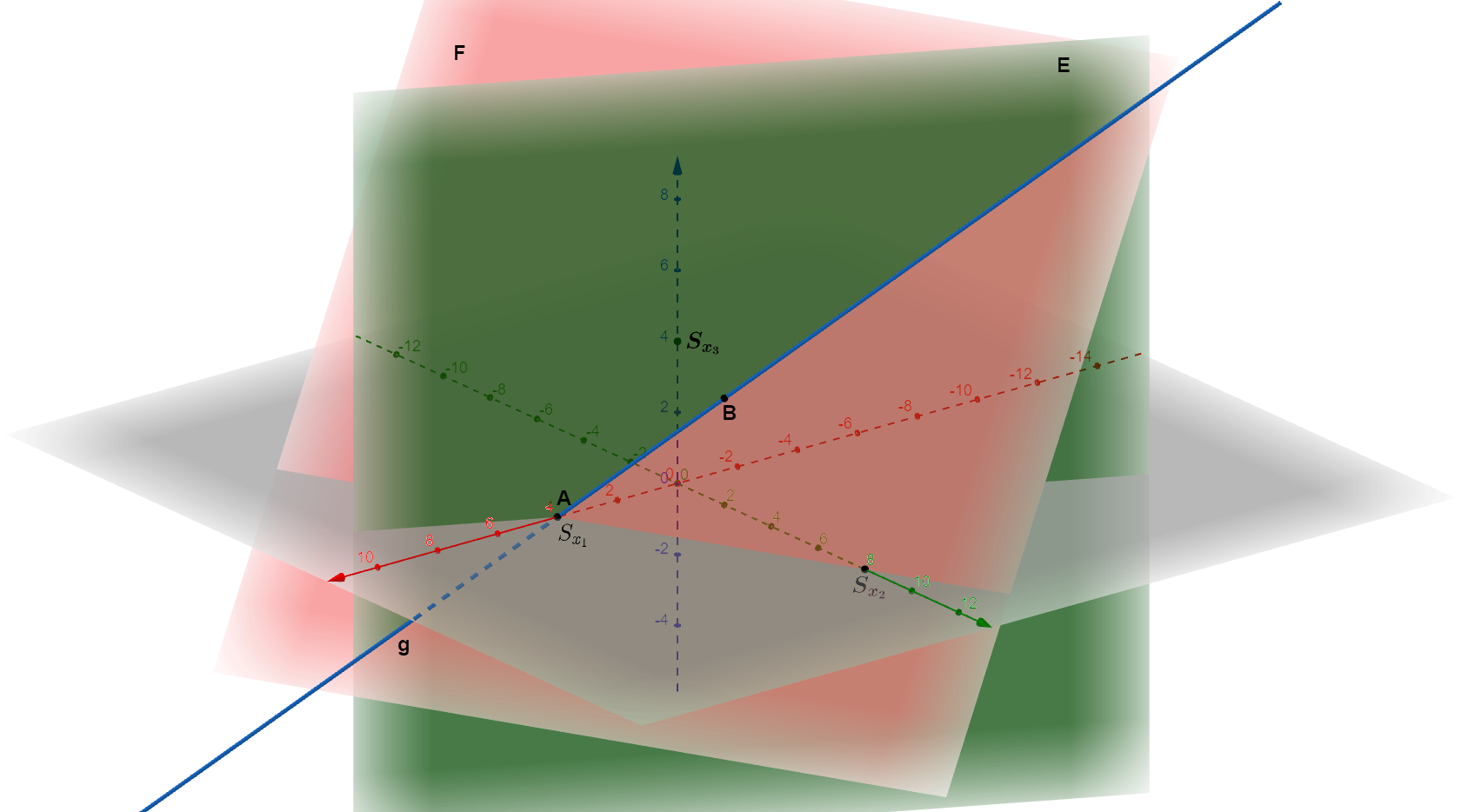
Die grüne Ebene ist die Ebene $E$ in Koordinatenform: $x_{1} + 2 x_{2} = 4$

In Achsenabschnittsform lautet $E$ : $\frac{x_{1}}{4} + \frac{x_{2}}{2} = 1$

So können die Achsenschnittpunkte (Spurpunkte) abgelesen werden: $S_{x_{1}} (4 | 0 | 0)$ ; $S_{x_{2}} (0 | 2 | 0)$

Es gibt keinen Schnittpunkt mit der $x_{3}$ -Achse, d.h. die Ebene $E$ verläuft parallel zur $x_{3}$ -Achse

Die rote Ebene ist die Ebene $F$ in Koordinatenform: $2 x_{1} + x_{2} + 2 x_{3} = 8$

In Achsenabschnittsform lautet $F$ : $\frac{x_{1}}{4} + \frac{x_{2}}{8} + \frac{x_{3}}{4} = 1$

So können die Achsenschnittpunkte abgelesen werden: $S_{x_{1}} (4 | 0 | 0)$ ; $S_{x_{2}} (0 | 8 | 0)$ ; $S_{x_{3}} (0 | 0 | 4)$

Lösung zu b)

Du suchst zwei Punkte, die in beiden Ebenen liegen.

Der Punkt $A (4 | 0 | 0) = S_{x_{1}}$ ist ein gemeinsamer Punkt der beiden Ebenen $E$ und $F$ .

Für alle Werte von $x_{3}$ liegt der Punkt $B (0 | 2 | x_{3})$ in der Ebene $E$ ( $B$ erfüllt die Ebenengleichung).

Damit $B$ auch in der Ebene $F$ liegt, muss gelten:

$B \in F \Rightarrow 2 \cdot 0 + 2 + 2 \cdot x_{3} = 8 \Rightarrow x_{3} = 3 \Rightarrow B (0 | 2 | 3)$

Die Schnittgerade ergibt sich dann zu: $g : \vec{X} = \vec{O A} + r \cdot \vec{A B}$

$g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot ((\begin{array}{c} 0 \\ 2 \\ 3 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 0 \end{array})) = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ 2 \\ 3 \end{array})$

Antwort: Die Gleichung der Schnittgeraden lautet: $g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ 2 \\ 3 \end{array})$

Aufgabe 6.5

Lösung zu a)

Die Ebene $E$ hat keinen Schnittpunkt mit der $x_{1}$ -Achse, d.h. die Ebenengleichung $E$ hat unter Berücksichtigung der gegebenen Spurpunkte die Achsenabschnittsform:

$E : \frac{x_{2}}{- 3} + \frac{x_{3}}{4} = 1 \Rightarrow - 4 x_{2} + 3 x_{3} = 12$

Antwort: Die Gleichung der Ebene $E$ lautet: $- 4 x_{2} + 3 x_{3} = 12$

Lösung zu b)

Die Ebene $E$ hat den Normalenvektor ${\vec{n}}_{E} = (\begin{array}{c} 1 \\ 0 \\ 0 \end{array})$ .

Da die Ebene $F$ parallel zu $E$ sein soll, hat sie den gleichen Normalenvektor wie $E$ und enthält den Punkt A.

$F : (\vec{x} - \vec{O A}) \circ {\vec{n}}_{E} = 0 \Rightarrow (\vec{x} - (\begin{array}{c} 3 \\ - 3 \\ - 1 \end{array})) \circ (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) = 0 \Rightarrow x_{1} - 3 = 0$

Antwort: Die Gleichung der Ebene $F$ lautet: $x_{1} = 3$ .

Lösung zu c)

Der Normalenvektor $\vec{n} = (\begin{array}{c} - 2 \\ 1 \\ 0 \end{array})$ der gegebenen Ebene $E$ ist der Richtungsvektor der Geraden $g$ ,

da die Gerade senkrecht zu $E$ steht.

Als Aufpunkt der Geraden $g$ wird der Punkt $P$ genommen.

Antwort: Die Gleichung der Geraden $g$ lautet: $\vec{X} = (\begin{array}{c} 5 \\ 1 \\ - 4 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ 0 \end{array})$

Aufgabe 6.6

Lösung zu a)

Wenn die beiden Richtungsvektoren Vielfache voneinander sind, dann gilt $g ∥ h$ :

${\vec{u}}_{g} = (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array})$ und ${\vec{u}}_{h} = (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array})$ $\Rightarrow {\vec{u}}_{h} = (- 3) \cdot {\vec{u}}_{g} \Rightarrow g ∥ h$

Der Aufpunkt der Geraden $g$ liegt nicht auf der Geraden $h$ , denn:

$(\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) = (\begin{array}{c} 4 \\ - 1 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array}) \Rightarrow (\begin{array}{c} 0 \\ 0 \\ - 1 \end{array}) \neq r \cdot (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array})$

Die letzte Gleichung ist für kein $r$ erfüllbar.

Antwort: Die beiden Geraden sind parallel, aber nicht identisch.

Lösung zu b)

Die gesuchte Ebene hat als Aufpunkt den Aufpunkt der Geraden $g$ und als einen Richtungsvektor den Richtungsvektor der Geraden $g$ . Einen zweiten Richtungsvektor der Ebene $E$ erhältst du als Differenz der beiden Aufpunkte der Geraden $g$ und $h$ .

$E : \vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot ((\begin{array}{c} 4 \\ - 1 \\ 1 \end{array}) - (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array})) = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$

Antwort: Die Gleichung der Ebene $E$ lautet: $\vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$

Aufgabe 7.1

Lösung zu a)

Die Ebenen sind parallel zueinander, wenn die Normalenvektoren parallel zueinander sind.

$\vec{a} \times \vec{b} = (\begin{array}{c} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{array}) \Rightarrow {\vec{n}}_{E} = (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array}) \times (\begin{array}{c} 1 \\ - 1 \\ - 2 \end{array}) = (\begin{array}{c} 1 \\ - 1 \\ 1 \end{array})$

Aus der Koordinatenform von der Ebene $F$ liest du den Normalenvektor ab:

${\vec{n}}_{F} = (\begin{array}{c} 1 \\ - 1 \\ 1 \end{array}) \Rightarrow {\vec{n}}_{E} = {\vec{n}}_{F}$

Die Ebenen sind parallel zueinander.

Lösung zu b)

Erstelle die Hessesche Normalenform der Ebene $F$ :

$F_{H N F} : \frac{a x_{1} + b x_{2} + c x_{3} + d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0 \Rightarrow \frac{x_{1} - x_{2} + x_{3} - 1}{\sqrt{3}} = 0$

Setze den Aufpunkt $A (1 | 2 | 3)$ der Ebene $E$ in die Hessesche Normalenform ein, um den Abstand der beiden Ebenen zu berechnen.

$d (A, F) = | \frac{1 \cdot 1 - 1 \cdot 2 + 1 \cdot 3 - 1}{\sqrt{1^{2} + (- 1)^{2} + 1^{2}}} | = | \frac{1}{\sqrt{3}} | = \frac{1}{\sqrt{3}} = \frac{1}{3} \cdot \sqrt{3}$

Antwort: Die beiden Ebenen haben einen Abstand von $\frac{1}{3} \cdot \sqrt{3}$ voneinander.

Aufgabe 7.2

Lösung zu a)

Für die Ebene in Parameterform gilt:

$E_{A B C} = \vec{O A} + r \cdot (\vec{O B} - \vec{O A}) + s \cdot (\vec{O C} - \vec{O A})$

$E_{A B C} = (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}) + r \cdot ((\begin{array}{c} 6 \\ 2 \\ 2 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) + s \cdot ((\begin{array}{c} 0 \\ 3 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}))$

$E_{A B C} = (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 3 \\ 3 \\ 4 \end{array})$

Bei der Umrechnung der Ebenengleichung in die Normalenform muss das Kreuzprodukt der beiden Richtungsvektoren der Ebene berechnet werden.

${\vec{n}}_{E} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) \times (\begin{array}{c} - 3 \\ 3 \\ 4 \end{array}) = (\begin{array}{c} 5 \\ - 15 \\ 15 \end{array})$

Der Normalenvektor kann noch vereinfacht werden: ${\vec{n}}_{E} = (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array})$

Mit dem Punkt $A (3 | 0 | 1)$ erhältst du dann die Normalenform der Ebene:

$E : (\vec{x} - \vec{O A}) \circ {\vec{n}}_{E} = 0 \Rightarrow (\vec{x} - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array}) = 0$

Wird das Skalarprodukt ausmultipliziert, erhältst du die Koordinatenform der Ebenengleichung:

$E : x_{1} - 3 x_{2} + x_{3} - (3 + 0 + 3) = 0 \Rightarrow x_{1} - 3 x_{2} + x_{3} - 6 = 0$

Antwort: Die Ebene in Normalenform hat die Gleichung $E : (\vec{x} - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array}) = 0$ und in Koordinatenform lautet sie: $E : x_{1} - 3 x_{2} + x_{3} = 6$

Lösung zu b)

Lageuntersuchung: $g \cap E$

Setze $g$ in $E$ ein:

$(4 + 2 t) - 3 (t) + 3 (1)$	$=$	$6$
	↓	Löse die Klammern auf
$4 + 2 t - 3 t + 3$	$=$	$6$
	↓	Löse nach $t$ auf.
$7 - t$	$=$	$6$	$- 7$
$- t$	$=$	$- 1$	$\cdot (- 1)$
$t$	$=$	$1$

Du hast für $t$ eine Lösung erhalten, d.h. die Gerade und die Ebene schneiden sich.

Berechnung des Schnittpunktes der Geraden mit der Ebene

Setze $t = 1$ in die Geradengleichung ein: ${\vec{x}}_{S} = (\begin{array}{c} 4 \\ 0 \\ 1 \end{array}) + 1 \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} 6 \\ 1 \\ 1 \end{array})$

Antwort: Die Gerade $g$ schneidet die Ebene $E$ im Punkt $S (6 | 1 | 1)$ .

Aufgabe 7.3

Lösung zu a)

Wenn die Geraden $g$ und $h$ orthogonal zueinander liegen sollen, dann muss das Skalarprodukt ihrer Richtungsvektoren gleich null sein.

${\vec{u}}_{g} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$ und ${\vec{u}}_{h} = (\begin{array}{c} 1 \\ 2 \\ 1 \end{array})$ $\Rightarrow {\vec{u}}_{g} \circ {\vec{u}}_{h} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \circ (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) = 2 + 2 - 4 = 0$

Antwort: Die Geraden $g$ und $h$ liegen orthogonal zueinander.

Lösung zu b)

Lageuntersuchung:

Setze $g = h$ :

$(\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) = (\begin{array}{c} 7 \\ 3 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array})$

Umgeformt erhältst du: $(\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) - (\begin{array}{c} 7 \\ 3 \\ 5 \end{array}) = s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) - t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$ bzw.

$(\begin{array}{c} - 4 \\ - 5 \\ 2 \end{array}) = s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) - t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$

Damit ergibt sich folgendes Gleichungssystem:

$\begin{array}{rccccccc} I & s & - & 2 t & = & - 4 \\ II & 2 s & - & t & = & - 5 \\ III & s & + & 4 t & = & 2 \end{array} $

Mit dem Additionsverfahren wird aus den Gleichungen $(I)$ und $(I I)$ der Parameter $s$ eliminiert.

Rechne dazu: $II + (- 2) \cdot I$ $\Rightarrow 3 t = 3 \Rightarrow t = 1$

Setze $t = 1$ in Gleichung $(I)$ ein $\Rightarrow s - 2 \cdot 1 = - 4 \Rightarrow s = - 2$

Probe in Gleichung $(I I I)$ : $s + 4 t = 2 \Rightarrow - 2 + 4 \cdot 1 = 2 ✓$

Zur Berechnung des Schnittpunktes setze $t = 1$ in die Geradengleichung $g$ ein:

${\vec{x}}_{S} = (\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) + 1 \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) = (\begin{array}{c} 5 \\ - 1 \\ 3 \end{array})$

Antwort: Die Geraden $g$ und $h$ schneiden sich im Punkt $S (5 | - 1 | 3)$ .

Aufgabe 7.4

Lösung zu a)

Wenn das Dreieck rechtwinklig ist, mit rechtem Winkel im Punkt $C$ , dann muss das Skalarprodukt $\vec{B C} \circ \vec{C A} = 0$ sein. Berechne die Vektoren $\vec{B C}$ und $\vec{C A}$ :

$\vec{B C} = (\begin{array}{c} 2 \\ 8 \\ 4 \end{array}) - (\begin{array}{c} 4 \\ 10 \\ 5 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ - 1 \end{array})$

$\vec{C A} = (\begin{array}{c} 12 \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 2 \\ 8 \\ 4 \end{array}) = (\begin{array}{c} 10 \\ - 8 \\ - 4 \end{array})$

Berechne das Skalarprodukt: $\vec{B C} \circ \vec{C A} = (\begin{array}{c} - 2 \\ - 2 \\ - 1 \end{array}) \circ (\begin{array}{c} 10 \\ - 8 \\ - 4 \end{array}) = - 20 + 16 + 4 = 0 ✓$

Antwort: Das Dreieck hat im Punkt $C$ einen rechten Winkel.

Lösung zu b)

Die Dreiecksfläche berechnet sich dann zu:

$A = \frac{1}{2} \cdot | \vec{B C} | \cdot | \vec{C A} | = \frac{1}{2} \cdot \sqrt{(- 2)^{2} + (- 2)^{2} + (- 1)^{2}} \cdot \sqrt{10^{2} + (- 8)^{2} + (- 4)^{2}} = \frac{1}{2} \cdot \sqrt{9} \cdot \sqrt{180} = \frac{3}{2} \cdot \sqrt{180} = \frac{3}{2} \cdot 6 \cdot \sqrt{5} = 9 \cdot \sqrt{5}$

Antwort: Das Dreieck hat einen Flächeninhalt von $9 \cdot \sqrt{5} FE$ .

Aufgabe 7.5

Für ein beliebiges Dreieck gilt die folgende Flächenformel: $A = \frac{1}{2} \cdot \sqrt{{\vec{a}}^{2} \cdot {\vec{b}}^{2} - (\vec{a} \circ \vec{b})^{2}}$

$\vec{a} = \vec{A B} = (\begin{array}{c} 3 \\ 7 \\ - 4 \end{array}) - (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 4 \\ - 4 \end{array})$

$\vec{b} = \vec{A C} = (\begin{array}{c} 2 \\ 8 \\ 1 \end{array}) - (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 1 \\ 5 \\ 1 \end{array})$

Eingesetzt in die Flächenformel:

$A = \frac{1}{2} \cdot \sqrt{{(\begin{array}{c} 2 \\ 4 \\ - 4 \end{array})}^{2} \cdot {(\begin{array}{c} 1 \\ 5 \\ 1 \end{array})}^{2} - {((\begin{array}{c} 2 \\ 4 \\ - 4 \end{array}) \circ (\begin{array}{c} 1 \\ 5 \\ 1 \end{array}))}^{2}}$

$A = \frac{1}{2} \cdot \sqrt{(4 + 16 + 16) \cdot (1 + 25 + 1) - (2 + 20 - 4)^{2}}$

$A = \frac{1}{2} \cdot \sqrt{36 \cdot 27 - 18^{2}} = \frac{1}{2} \cdot \sqrt{648} = \frac{1}{2} \cdot 18 \cdot \sqrt{2} = 9 \cdot \sqrt{2}$

Antwort: Das Dreieck hat einen Flächeninhalt von $9 \cdot \sqrt{2} FE$ .

Aufgabe 7.6

Lösung zu a)

Berechne die Beträge der Vektoren $\vec{A B}$ , $\vec{B C}$ und $\vec{A C}$

$\vec{A B} = (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) | = \sqrt{2^{2} + 3^{2} + 0^{2}} = \sqrt{13}$

$\vec{B C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) | = \sqrt{1^{2} + (- 3)^{2} + (- 2)^{2}} = \sqrt{14}$

$\vec{A C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}) | = \sqrt{3^{2} + 0^{2} + (- 2)^{2}} = \sqrt{13}$

$| \vec{A B} | = | \vec{A C} | \neq | \vec{B C} |$ , d.h. das Dreieck ist gleichschenklig, mit der Basis $[B C]$ .

Lösung zu b)

$[B C]$ ist die Basis des gleichschenkligen Dreiecks, d.h. der Punkt $P$ muss $A$ gegenüberliegen; siehe Skizze.

Du kannst die folgende Vektorgleichung aufstellen, um $P$ zu berechnen.

$\vec{O P} = \vec{O C} + \vec{A B} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) + (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ 3 \\ - 1 \end{array})$

Der Punkt $P$ hat die Koordinaten $P (- 2 | 3 | - 1)$ .

Lösung zu c)

Für ein beliebiges Dreieck gilt die folgende Flächenformel: $A = \frac{1}{2} \cdot \sqrt{{\vec{a}}^{2} \cdot {\vec{b}}^{2} - (\vec{a} \circ \vec{b})^{2}}$

$\vec{a} = \vec{B C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array})$

$\vec{b} = \vec{A C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array})$

Eingesetzt in die Flächenformel:

$A = \frac{1}{2} \cdot \sqrt{{(\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array})}^{2} \cdot {(\begin{array}{c} 3 \\ 0 \\ - 2 \end{array})}^{2} - {((\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) \circ (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}))}^{2}}$

$A = \frac{1}{2} \cdot \sqrt{(1 + 9 + 4) \cdot (9 + 0 + 4) - (3 + 0 + 4)^{2}}$

$A = \frac{1}{2} \cdot \sqrt{14 \cdot 13 - 7^{2}} = \frac{1}{2} \cdot \sqrt{133}$

Antwort: Das Dreieck $A B C$ hat einen Flächeninhalt von $\frac{1}{2} \cdot \sqrt{133} FE$ .

Aufgabe 9.1

1. Wähle einen beliebigen Punkt $P_{1} \in E_{1}$ .

2. Wähle einen beliebigen Punkt $P_{2} \in E_{2}$ .

3. Berechne den Mittelpunkt $M$ der Strecke $[P_{1} P_{2}]$ .

$\vec{O M} = \frac{1}{2} \cdot (\vec{O P_{1}} + \vec{O P_{2}})$

4. Nimm von den Ebenen $E_{1}$ oder $E_{2}$ einen der beiden Normalenvektoren z.B. ${\vec{n}}_{E_{1}}$ .

5. Setze in die Normalenform ein:

$F : (\vec{x} - \vec{O M}) \circ {\vec{n}}_{E_{1}} = 0$ .

Aufgabe 9.2

Gegeben $E : a x_{1} + b x_{2} + c x_{3} - d = 0$

$\Rightarrow \vec{n_{E}} = (\begin{array}{c} a \\ b \\ c \end{array})$

Der dazugehörende Normaleneinheitsvektor ist dann:

$\vec{n_{E}^{0}} = \frac{1}{\sqrt{a^{2} + b^{2} + c^{2}}} \cdot (\begin{array}{c} a \\ b \\ c \end{array})$

Finde einen Punkt $Q \in E$ . Dann führt die Vektorgleichung $\vec{O P} = \vec{O Q} + 3 \cdot \vec{n_{E}^{0}}$ zu einem Punkt $P \in F$ .

Da $F ∥ E$ ist $\vec{n_{F}} = \vec{n_{E}}$ . Mit dem Punkt $P$ kann die Gleichung der Ebene $F$ in Normalenform angegeben werden.

$F : (\vec{x} - \vec{O P}) \circ {\vec{n}}_{E} = 0$

Aufgabe 9.3

Erstelle eine Parameterform der Ebene $E$ , in der das Parallelogramm liegt.

z.B. $E : \vec{x} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A D}$

Prüfe, ob $P \in E$ ?

$(I) \vec{O P} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A D}$

1. Gleichung $(I)$ hat keine Lösung, dann gilt $P \notin E$ und $P \notin □$ .

2. Gleichung $(I)$ hat eine Lösung, dann gilt $P \in E$ und $P \in □$ , wenn die Bedingung $0 \leq r, s \leq 1$ erfüllt ist.

Aufgabe 9.4

Lösung zu a)

Das Schaubild der Funktion kann z.B. so wie in der Abbildung aussehen.

Es hat folgende Eigenschaften:

$f (x) > 0$ (alle Funktionswerte liegen oberhalb der $x$ -Achse)

$f^{'} (x) > 0$ (die Steigung ist immer positiv)

$f^{''} (x) < 0$ (Der Graph ist rechtsgekrümmt)

Lösung zu b)

Es gilt: $f^{''} (x) < 0 \Leftrightarrow (f^{'} (x))^{'} < 0 \Rightarrow f^{'} (x)$ ist streng monoton fallend. Fällt die Steigung eines Funktionsgraphen permanent, dann ist der Graph rechtsgekrümmt.

Aufgabe 9.4

Ein Bernoulli-Experiment wird $15$ -mal durchgeführt ( $n = 15$ ). Dabei ist die Erfolgswahrscheinlichkeit $p = 0,6$ und $q = 1 - p = 0,4$ .

Ereignis $A$ : Es gibt höchstens $12$ Erfolge bei $15$ Wiederholungen.

(alternative Formulierung: Es gibt weniger als $13$ Erfolge bei $15$ Wiederholungen)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu c)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lageuntersuchung: g∩E

Berechnung des Schnittpunktes der Geraden mit der Ebene

Lösung zu a)

Lösung zu b)

Lageuntersuchung:

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu c)

Lösung zu a)

Lösung zu b)

Lageuntersuchung: $g \cap E$