Kowalskys Testaufgabe
Lösung von Gleichungen-Übersicht
In einem Multiple-Choice-Test gibt es Aufgaben, bei denen man aus drei möglichen Lösungen die richtige ankreuzen muss. Felix hat sich nicht auf den Test vorbereitet. Mit welcher Wahrscheinlichkeit wird er trotzdem genau die Hälfte der Fragen richtig beantworten?
Gegeben ist der Kreis . Durch den Punkt verläuft eine Gerade , die Tangente an den Kreis sein soll. Berechne die Funktionsgleichung der Geraden und den Berührpunkt .
Welche Punkte sind Berührpunkte (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich nicht im Schnittpunkt)?
Gegeben ist ein Quader mit den Seiten , und .
Aus einer Quaderecke wird eine Pyramide herausgeschnitten. Die Schnitte verlaufen längs der Diagonalen der Seitenflächen.
a) Berechne jeweils die Flächeninhalte der vier Dreiecke , , und .
Hinweis: Verwende die Bezeichnungen von Bild 1 und Bild 3 und verwende für die Berechnung des Flächeninhalts von den Kosinussatz.
b) Weise nach, dass gilt.
Gegeben ist eine Ebenenschar mit .
a) Die beiden Ebenen und sollen senkrecht aufeinander stehen.
Welche Beziehung besteht zwischen und ?
b) Zu welcher Ebene aus der oben angegebenen Schar gibt es keine dazu senkrechte Ebene aus dieser Schar?
c) Es ist . Berechne den Abstand des Koordinatenursprungs von der Scharebene und gib gegebenenfalls den Grenzwert an.
Beziehungen zwischen den Winkelfunktionen
gegeben
gegeben
gegeben
Beziehungen zwischen Sinus, Kosinus, Tangens und Kotangens
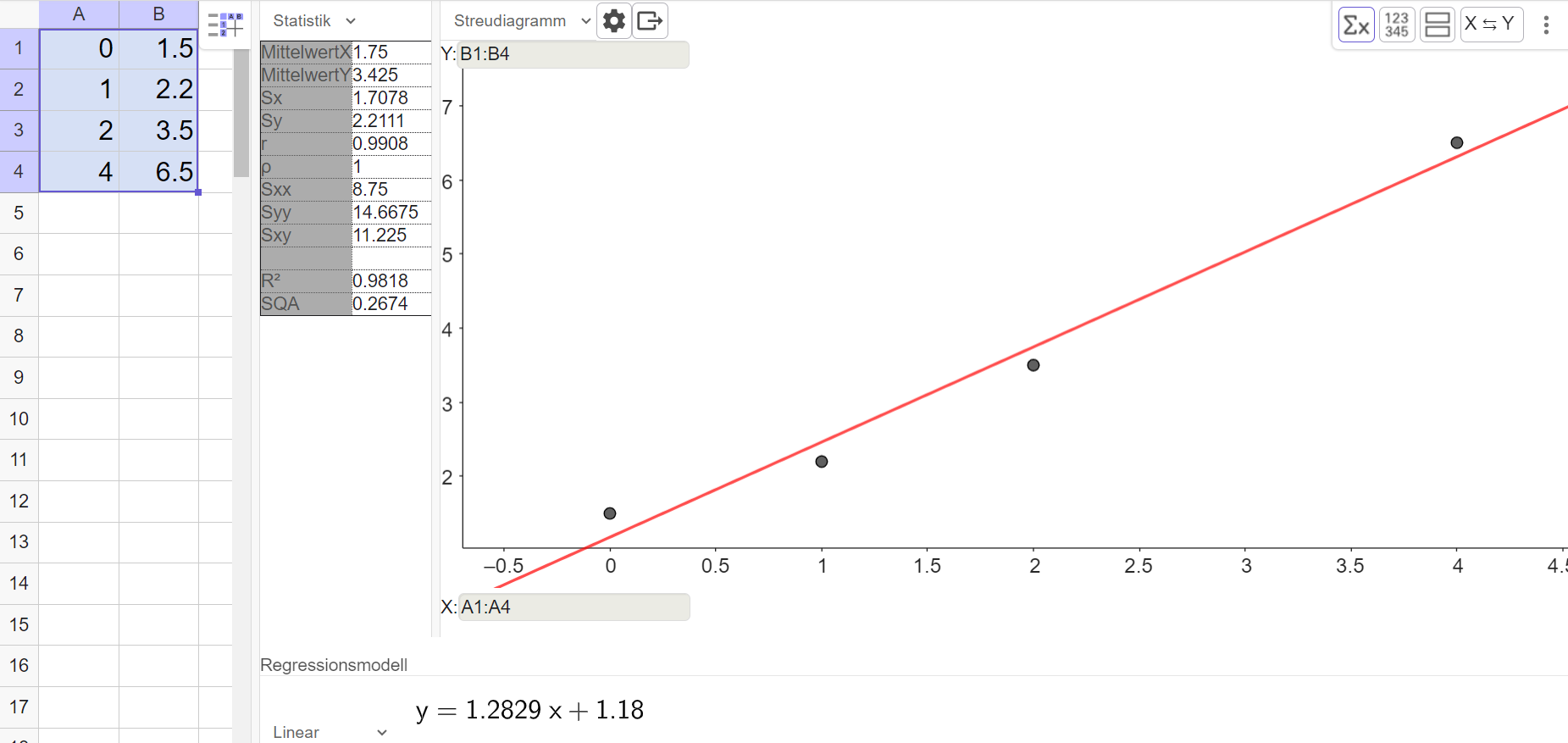
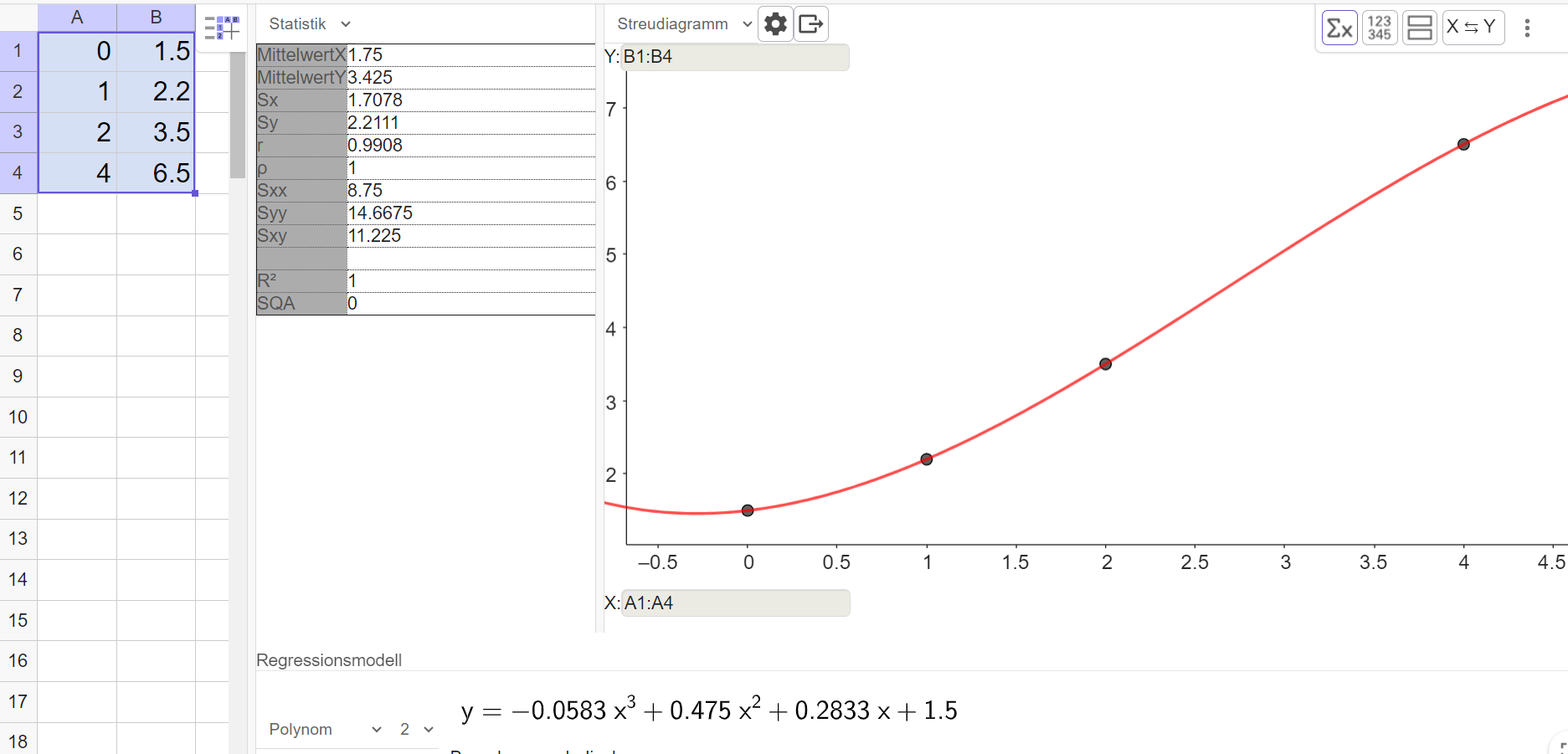
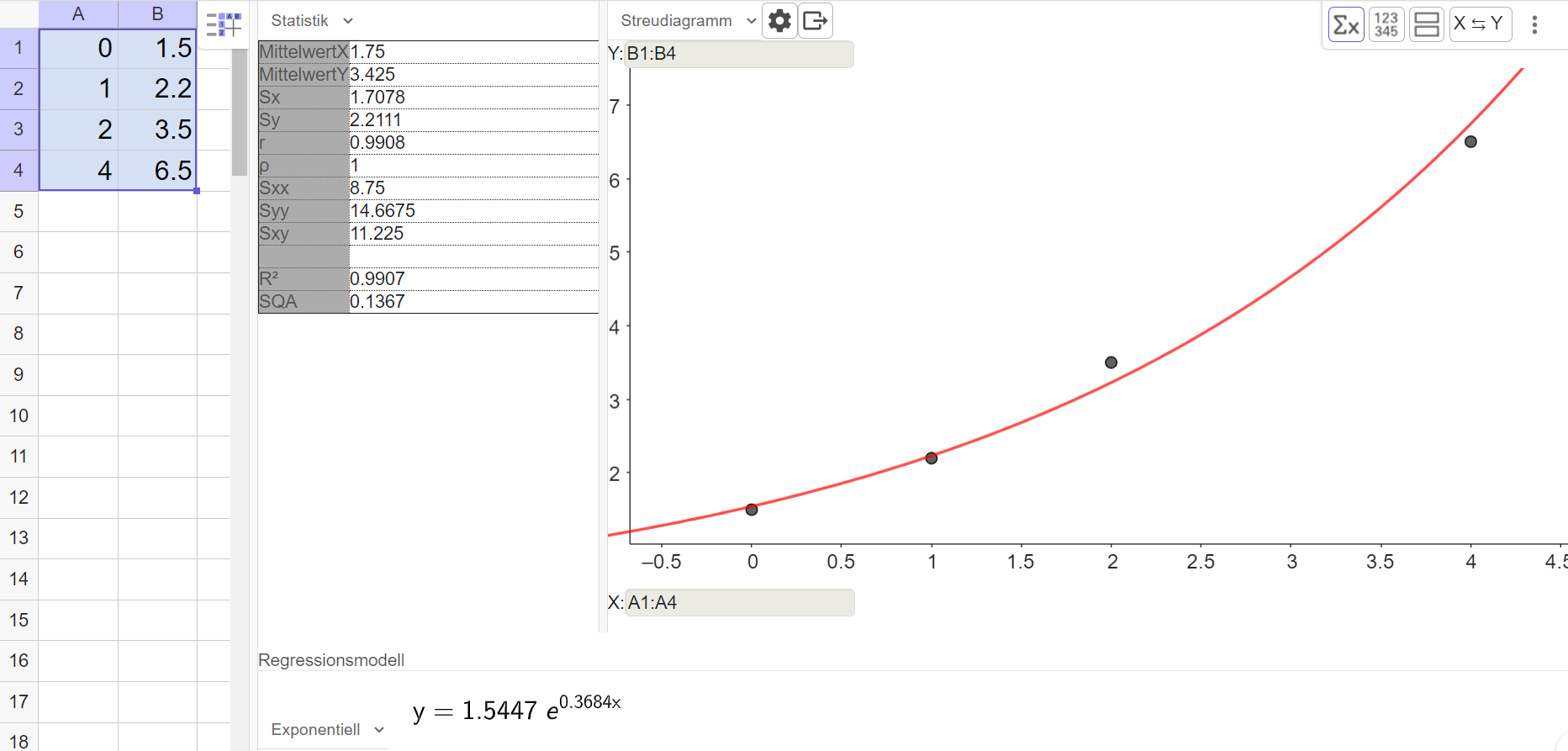
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?