Einführung in den verminderten und vermehrten Grundwert

1 Übersicht

Inhalt des Kurses

Du weißt jetzt bereits, was die Begriffe Grundwert, Prozentsatz und Prozentwert bedeuten und wie man mit ihnen rechnet. Ziel dieses Kurses ist es, dein Wissen über Prozentrechnung in neuen Situationen anzuwenden. Im Folgenden werden dir solche Situationen vorgestellt und neue Rechenmethoden eingeführt. Außerdem lernst du die Begriffe verminderter Grundwert, vermehrter Grundwert und Wachstumsfaktor kennen.

Vorkenntnisse

Du solltest die Umrechnung der drei Zahldarstellungen (Bruchzahl, Dezimalzahl, Prozentzahl) beherrschen.
Der Kurs Einführung des Prozentzeichens und seiner Umrechnung gilt als Grundvoraussetzung für diesen Kurs.
Dieser Kurs baut unmittelbar auf den Kurs Einführung in Grundwert, Prozentwert und Prozentsatz auf. Dort lernst du das Prozentrechnen mit Grundwert, Prozentwert und Prozentsatz.

Kursdauer

Der Kurs dauert ungefähr 2-3 Stunden (wenn du alle Aufgaben selbstständig lösen möchtest).

2 Verminderte und vermehrte Grundwerte im Alltag

Läden locken ihre Kunden oft mit Rabattaktionen.

Auf Produktverpackungen liest man oft Sprüche wie " $+ 33 %$ mehr Inhalt"

Wie du vielleicht schon weißt, kosten Kleidungsstücke oder andere Produkte, die um $50 %$ reduziert sind, nur noch die Hälfte.

Solche Packungen enthalten offensichtlich mehr als üblich. Doch wie viel genau?

Doch wie viel kostet ein Produkt, das um $20 %$ reduziert wurde?

Und wenn es auf einen Pullover, der schon um $50 %$ reduziert wurde, noch einmal $50 %$ Rabatt gibt - ist er dann kostenlos?

Ist eine Pflanze, die in der ersten Woche um $100\ \%$ wächst und in der zweiten Woche wieder um $100\ \%$ wächst, dann dreimal so groß wie am Anfang?

3 Hinführung zum Umgang mit verminderten/ vermehrten Grundwerten

Erinnere dich: Die Begriffe Grundwert $G$ , Prozentwert $W$ und Prozentsatz $p$ hast du schon kennengelernt. Mithilfe der Formel $W = p \cdot G$ und dem Dreisatz kannst du schon einige Aufgaben zur Prozentrechnung lösen.

Beispielaufgabe 1

Ein Paar Sportschuhe kostet normalerweise $40 €$ .

Die Schuhe kosten dich jetzt noch $40\ €-8\ €=32\ €$ . Der Grundwert wurde also um $20 %$ bzw. $8 €$ vermindert. Den neuen Preis nennt man den verminderten Grundwert $\text{G}^-$ .

Beispielaufgabe 2

In einer Packung sind $200\ g$ Cornflakes. In der Aktionspackung ist laut Werbung $10 %$ mehr Inhalt. Wie viel Gramm Cornflakes sind zusätzlich in dieser Aktionspackung?

Gegeben: $G=200\ g$ ; $p=10\ \%$

Gesucht: $W$

Lösung: $W=p\cdot G=10\ \%\cdot200\ g=0{,}1\cdot200\ g=20\ g$

Antwort: In der Aktionspackung sind $20\ g$ mehr Cornflakes.

In der Aktionspackung sind insgesamt $200\ g+20\ g=220\ g$ Cornflakes. Der Grundwert wurde also um $10 %$ bzw. $20\ g$ erhöht. Die neue Grammzahl nennt man den vermehrten Grundwert $\text{G}^+$ .

4 Übungsaufgaben zum Einstieg

Löse folgende Aufgaben wie die vorangehenden Beispielaufgaben.

Laden

5 Anschauliche Darstellung

Hier wird dir das Prinzip des verminderten / vermehrten Grundwerts anschaulich dargestellt.

1. Verminderter Grundwert

Der verminderte Grundwert ergibt sich, indem du den Prozentwert vom Grundwert subtrahierst.

$G^{-} = G - W$

Der Grundwert wird also um den Prozentwert reduziert.

2. Vermehrter Grundwert

Der vermehrte Grundwert ergibt sich, indem du Grundwert und Prozentwert addierst.

$G^{+} = G + W$

Der Grundwert wird also um den Prozentwert erhöht.

Die Entscheidung, ob der Grundwert erhöht oder vermindert werden muss, triffst du aufgrund der Aufgabenstellung.

Übungsaufgabe

Laden

6 Verminderter Grundwert

Es gibt einen weiteren Aufgabentyp, den du mit deinem jetzigen Wissen noch nicht lösen kannst.

Beispielaufgabe

Beim Braten von Fleisch gehen ca. $25 %$ des Gewichtes beim Erhitzen verloren. Wie viel Fleisch muss eingekauft werden, wenn das Fleisch nach dem Braten $180\ g$ wiegen soll?

Ordne den angegebenen Zahlen ihre passenden Fachbegriffe zu. (Tipp: Beim Erhitzen des Fleisches geht Gewicht verloren. Die $180\ g$ nach dem Braten entsprechen also einem verminderten Grundwert.)

$\Rightarrow$ Gegeben:

$p=25\ \%$

$G^-=180\ g$

Gib die gesuchte Größe an.

$\Rightarrow$ Gesucht: $G$

Wende die Formel an.

$\Rightarrow$ $G=\frac{W}{P}$

Um die Aufgabe zu lösen, musst du dein Wissen "umsortieren"!

Der Grundwert $G$ entspricht $100\ \%$

Eine wichtige Erkenntnis ist, dass $G^-~\widehat{=}~100~\%-25~\%= 75~\%$

In der Aufgabe ist aber nach dem Grundwert gefragt. Wozu also die Überlegung?

Wenn wir wissen, dass $180~g=G~\widehat{=}~ 75~\%$ , können wir mit dem uns bekannten Wissen ausrechnen, welcher Wert $100\ \%$ entspricht.

Gelöst wird das wieder mit dem Dreisatz:

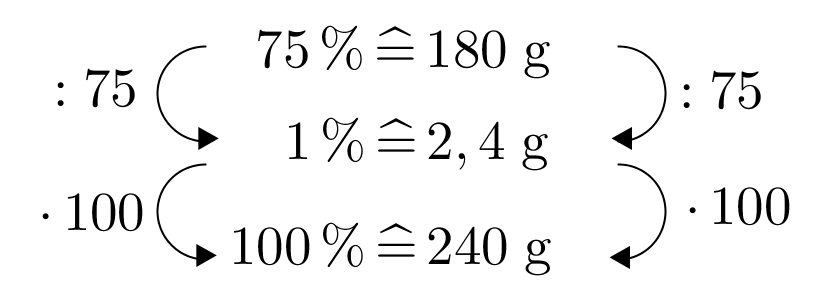
Jetzt weißt du: $G = 240 g$ .

Antwort: Du musst also ein Fleischstück von $240 g$ kaufen, damit nach dem Braten noch $180 g$ übrig bleiben.

7 Gleiche Lösung, kürzerer Weg!

Im Folgenden lernst du, wie du diesen Rechenweg abkürzt.

Dazu musst du zuerst dein jetziges Wissen verwenden.

Du weißt: $G^{-} = G - W$ und $W = p \cdot G$

Jetzt kannst du die beiden Formeln zusammenbringen, indem du statt des Prozentwerts $W$ das Produkt aus Prozentsatz $p$ und Grundwert $G$ einsetzt:

$\mathrm G^-=\mathrm G-\underbrace {\text{W}}_{=\mathrm p \cdot \mathrm G}$

$\mathrm G^-=\mathrm G-\mathrm p\cdot\mathrm G$

Du kannst G nun ausklammern:

$G^- = G - p \cdot G = G \cdot 1 - G \cdot p = G \cdot (1 - p)$

$G^- = G \cdot (1 - p)$

Kürzerer Weg:

Bezogen auf das vorherige Beispiel bedeutet das:

$G^{-} = G (1 - p)$

$180~ g = G (1 - 25~\%) = G (1 - 0{,}25) = G \cdot 0{,}75$

$\Rightarrow$ $G = 180 g : 0,75 = 240 g$

Skizze eines Schildes mit der Aufschrift "Abkürzung"

Merke

Man nennt $(1 - p)$ auch den Wachstumsfaktor, den man für den verminderten Grundwert verwendet. Es gilt $G^{-} = G (1 - p)$ .

8 Übungsaufgaben zum verminderten Grundwert

Am Anfang dieses Kurses wurden Fragen in den Raum gestellt, die du nun beantworten kannst.

Laden

9 Vermehrter Grundwert

Beispielaufgabe

Im Jahre 2012 ist die Anzahl der verkauften Smartphones in Deutschland im Vergleich zum Vorjahr um etwa $36 %$ auf 21,6 Millionen Stück gestiegen. Wie viele Smartphones wurden 2011 verkauft?

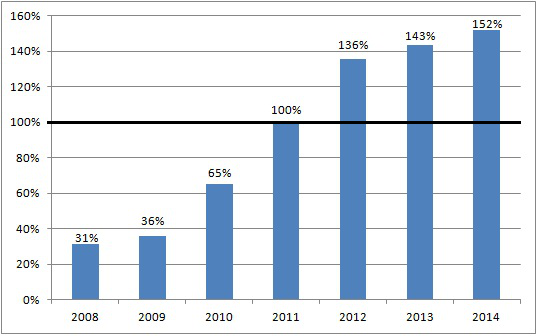
Es handelt sich bei der Verkaufszahl von 2012 um eine Steigerung ausgehend von 2011, also müssen die 21,6 Millionen von 2012 ein vermehrter Grundwert sein.

Gegeben: $p = 36~\%$ ; $G$ $^{+}$ = $21,6$ Millionen

Gesucht: $G$

Ähnlich wie schon beim verminderten Grundwert kommst du mit der bekannten Formel $G= \frac{W}{p}$ nicht weiter.

Wieder musst du dein Wissen "umsortieren", um die Lösung zu finden.

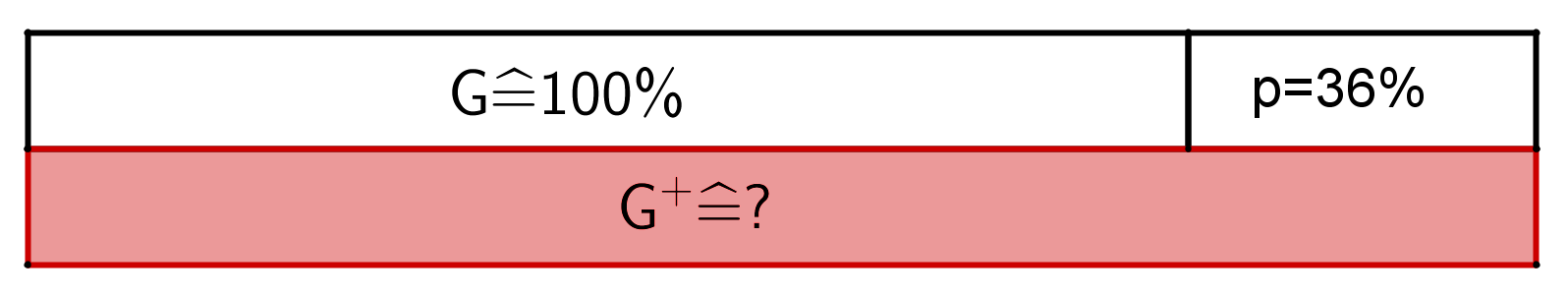
Du kannst erkennen: $G$ $^+ \widehat=$ $100~\% + 36~\% = 136~\%$

In der Aufgabe ist aber nach dem Grundwert $G$ gefragt.

Wir wissen: 21,6 Millionen = $G$ $^+ \widehat=$ $136~\%$

Löse nun mit dem Dreisatz:

Jetzt weißt du: $G = 15882352,9$ Smartphones

Runde das Ergebnis auf Millionen und eine Nachkommastelle, damit dein Ergebnis zu der Angabe passt.

Antwort: Im Jahre 2011 wurden ca. 15,9 Millionen Smartphones verkauft.

Alternativlösung (wieder eine Art Abkürzung)

Du weißt: $G^+= G + W ; W = p \cdot G$

Jetzt kannst du die beiden Formeln zusammenbringen, indem du für den Prozentwert $W$ das Produkt aus Prozentsatz $p$ und dem Grundwert $G$ einsetzt.

$G$ $^{+}$ $= G + W = G + (p \cdot G) = G + p \cdot G$

Du kannst $G$ ausklammern

$G^{+}$ $= G \cdot 1 + p \cdot G = G (1 + p)$

Wendest du diese Erkenntnis auf die Aufgabe von oben an. Erhältst du:

$G$ $^{+}$ $= G (1 + p)$

$21,6$ Millionen $= G (1 + 36~\%) = G (1 + 0{,}36)$

$21,6$ Millionen $= G \cdot 1{,}36$

$\Rightarrow$ $G =$ $21,6$ Millionen $: 1,36$

$\Rightarrow$ $G = 15,9$ Millionen

Merke

Man nennt $(1 + p)$ auch den Wachstumsfaktor, den man für den vermehrten Grundwert verwendet. Es gilt $G$ $^{+}$ $= G (1 + p)$ .

10 Übungsaufgaben zum vermehrten Grundwert

Am Anfang dieses Kurses wurden Fragen in den Raum gestellt, die du nun beantworten kannst.

Laden

11 Zusammenfassung

Wachstumsfaktor

Mit dem Wachstumsfaktor beschreibt man eine prozentuale Änderung.

$\Rightarrow$ Für den verminderten Grundwert ist der Wachstumsfaktor $(1 - p)$ und somit kleiner als 1. Wenn eine Größe z.B. um $5 %$ abnimmt, wird sie auf das 0,95-fache verringert.

$\Rightarrow$ Für den vermehrten Grundwert ist der Wachstumsfaktor $(1 + p)$ und somit größer als 1. Wenn eine Größe z.B. um $7 %$ zunimmt, wird sie auf das 1,07-fache erhöht.

Verminderter Grundwert

$G^-=G-W=G\cdot(1-p)$

Vermehrter Grundwert

$G^+=G+W=G\cdot(1+p)$

12 Zeig, was du kannst!

Laden

Hier findest du weitere Aufgaben zu vermehrtem und vermindertem Grundwert.