8Winkel
Man kann jetzt den Winkel zwischen zwei Vektoren bestimmen. Das geschieht immer gegen den Uhrzeigersinn.*
Rechts im Bild kannst du sehen, dass es dafür zwei Möglichkeiten gibt: Den kleineren Winkel und den größeren Winkel . Man gibt aber normalerweise immer nur den kleineren an.
Es gilt immer: .
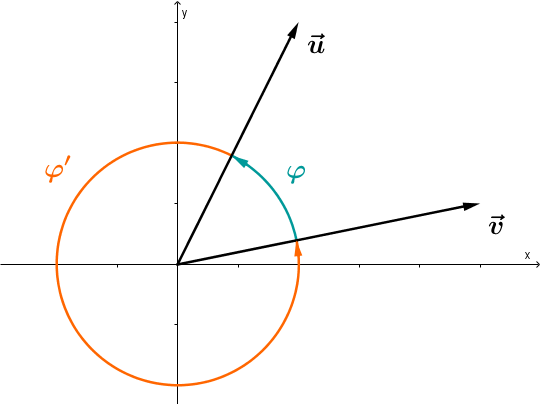
Die Berechnung des Winkels zwischen und geht folgendermaßen:
beziehungsweise
Der größere Winkel lässt sich dann so berechnen:
Dabei steht das "" für das Skalarprodukt.
"" ist die inverse Kosinus-Funktion: der Arkuskosinus. Das bedeutet insbesondere, dass
