Spiegle den Punkt an der Ursprungsgeraden und gib die Koordinaten des Bildpunktes an.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
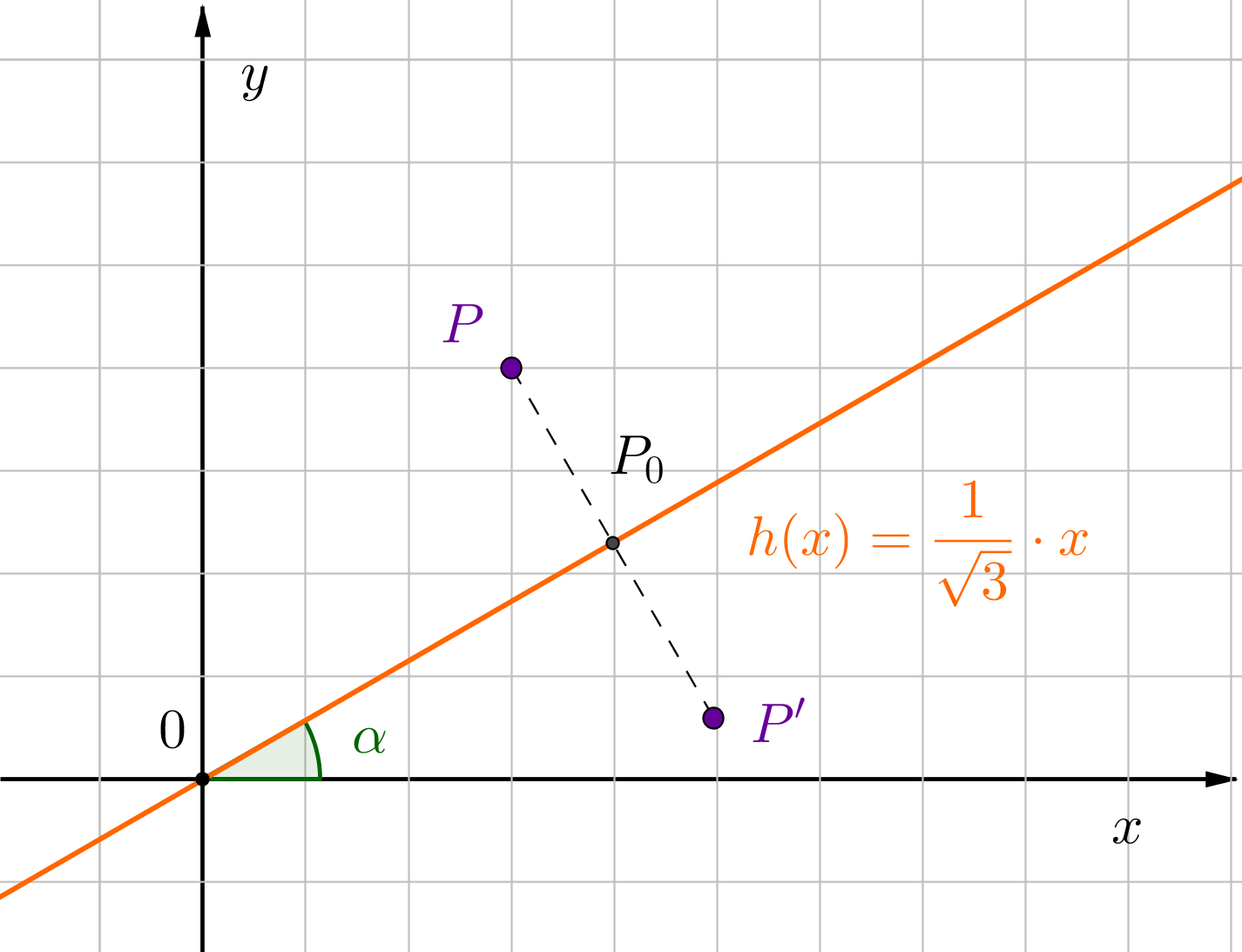
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
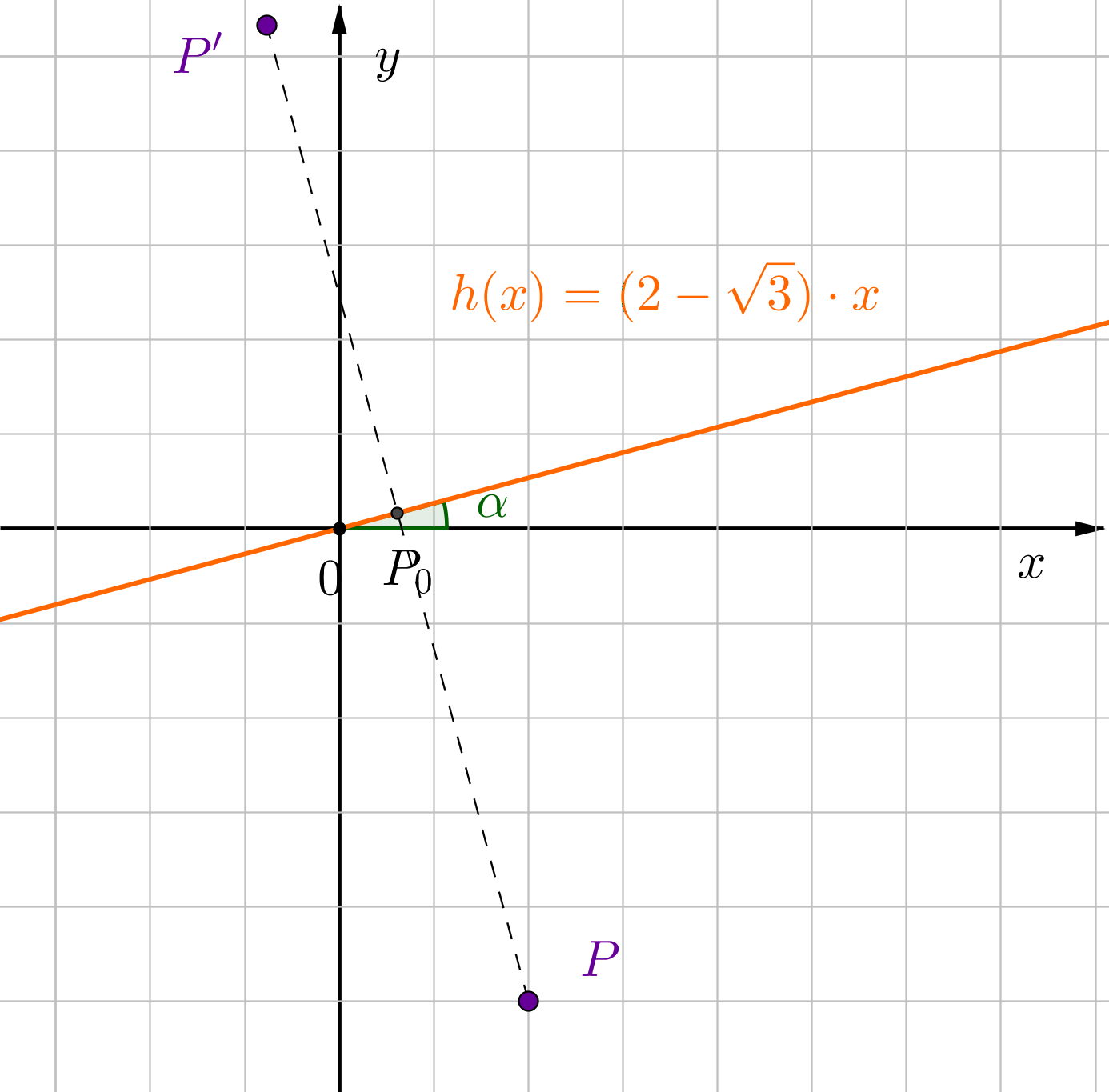
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
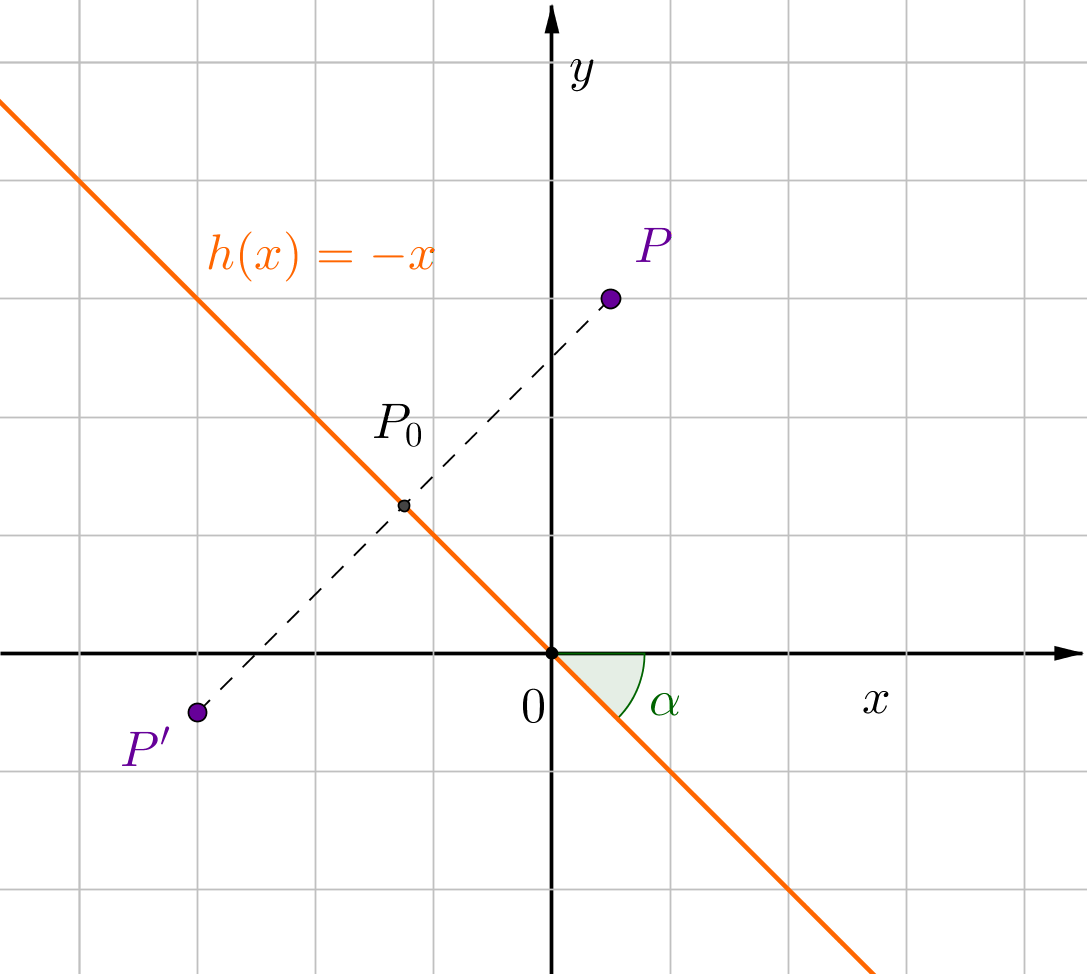
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
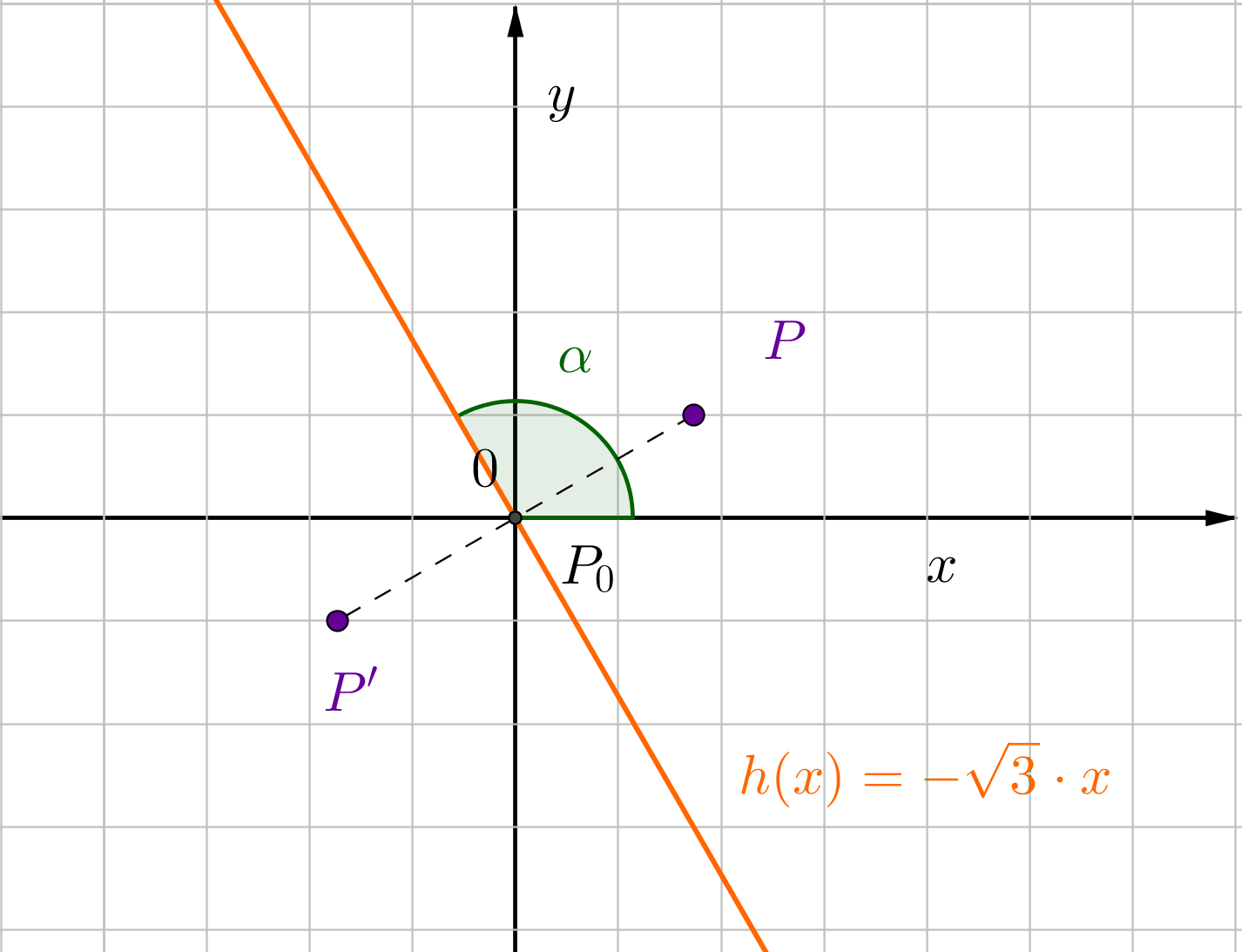
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
