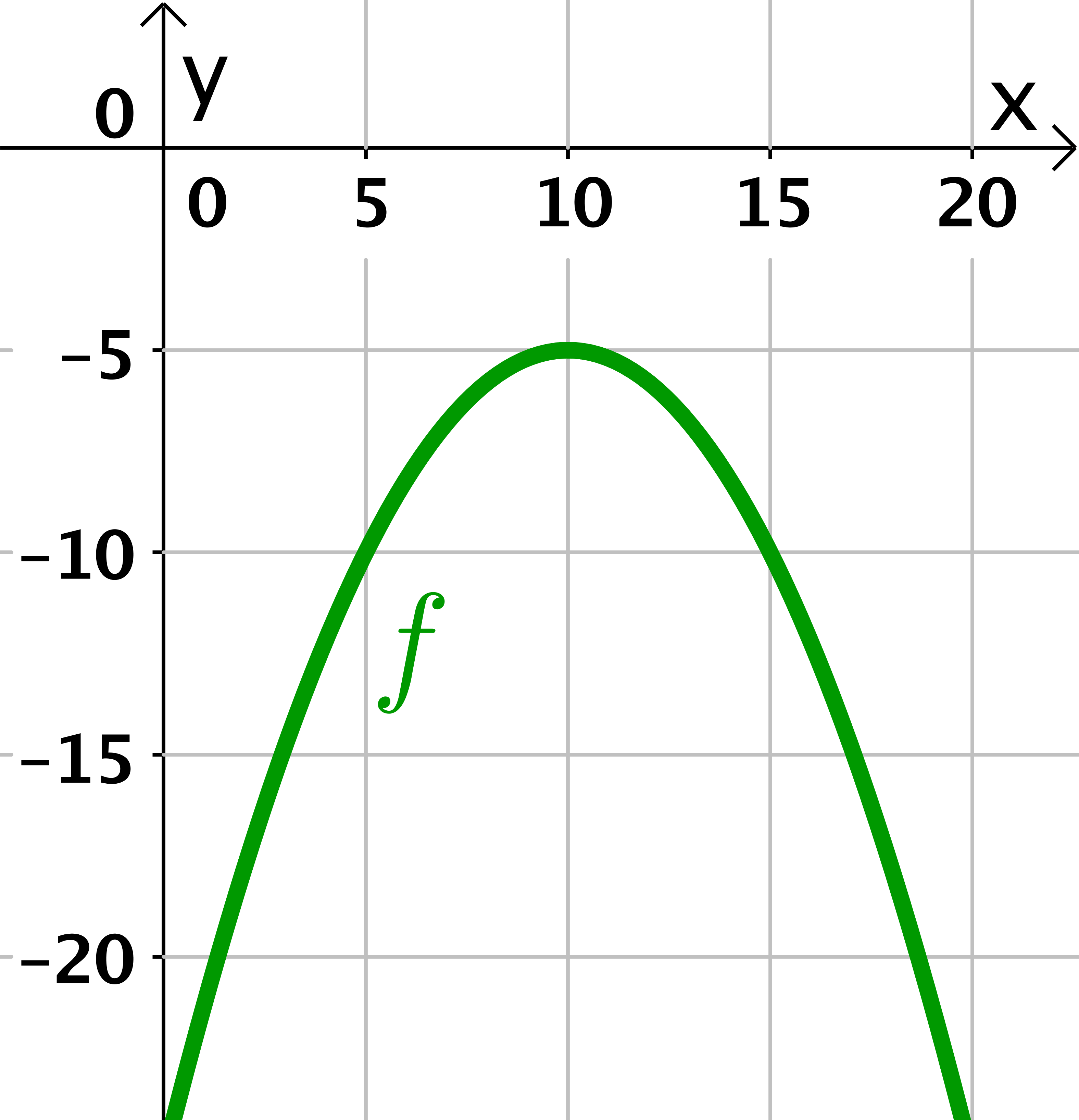
Wähle anhand der nebenstehenden Parabel die zugehörige Funktionsgleichung zu dem Graphen aus.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Wähle anhand der nebenstehenden Parabel die zugehörige Funktionsgleichung zu dem Graphen aus.
