Folgende Vorgehensweise hilft dir bei Graphen zu Exponentialfunktionen $f(x)=a\cdot b^x$:

• Ist $b>1$ werden die Funktionswerte betragsmäßig immer größer. D.h. sie entfernen sich von der Null

• Ist $b<1$ nähern sich die Werte immer mehr an die Null an. (für größer werdende x-Werte)

• Ist $a$ positiv, hat die Funktion nur positive Werte.

• Ist $a$ negativ, hat die Funktion nur negative Werte. (Die Funktion wurde an der x-Achse gespiegelt.)

In dieser Aufgabe:

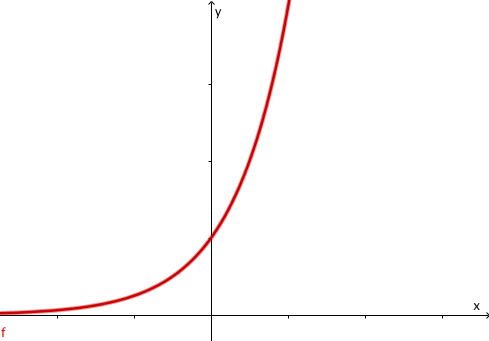
Die Funktion steigt immer steiler an (die x-Werte werden immer größer) $\Rightarrow b>1$. Die Funktion hat nur positve Werte $\Rightarrow a>0$. Der richtige Term ist $1\cdot4^x$.

Folgende Vorgehensweise hilft dir bei Graphen zu Exponentialfunktionen $f(x)=a\cdot b^x$:

• Ist $b>1$ werden die Funktionswerte betragsmäßig immer größer. D.h. sie entfernen sich von der Null

• Ist $b<1$ nähern sich die Werte immer mehr an die Null an. (für größer werdende x-Wert)

• Ist $a$ positiv, hat die Funktion nur positive Werte.

• Ist $a$ negativ, hat die Funktion nur negative Werte. (Die Funktion wurde an der x-Achse gespiegelt.)

In dieser Aufgabe:

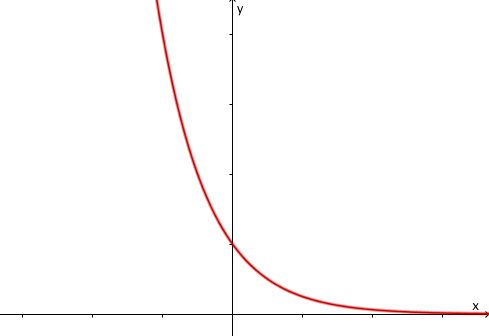
Die Funktionswerte nähern sich der x-Achse $\Rightarrow 0<b<1$. Die Funktion hat nur positve Werte $\Rightarrow a>0$. Der richtige Term ist $\;1\cdot\left({1\over4}\right)^x$.

Folgende Vorgehensweise hilft dir bei Graphen zu Exponentialfunktionen $f(x)=a\cdot b^x$:

• Ist $b>1$ werden die Funktionswerte betragsmäßig immer größer. D.h. sie entfernen sich von der Null

• Ist $b<1$ nähern sich die Werte immer mehr an die Null an. (für größer werdende x-Wert)

• Ist $a$ positiv, hat die Funktion nur positive Werte.

• Ist $a$ negativ, hat die Funktion nur negative Werte. (Die Funktion wurde an der x-Achse gespiegelt.)

In dieser Aufgabe:

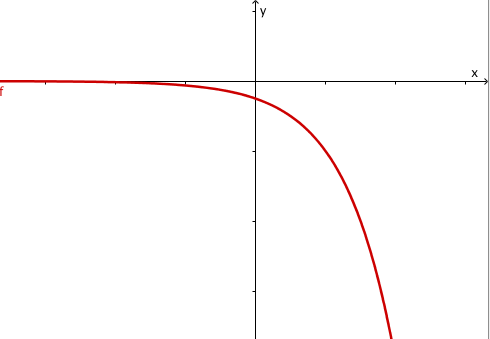
Die Funktionswerte entfernen sich von der x-Achse $\Rightarrow b>1$. Die Funktion hat nur negative Werte $\Rightarrow a<0$. Der richtige Term ist $-{1\over2}\cdot2^x$.

Folgende Vorgehensweise hilft dir bei Graphen zu Exponentialfunktionen $f(x)=a\cdot b^x$:

• Ist $b>1$ werden die Funktionswerte betragsmäßig immer größer. D.h. sie entfernen sich von der Null

• Ist $b<1$ nähern sich die Werte immer mehr an die Null an. (für größer werdende x-Wert)

• Ist $a$ positiv, hat die Funktion nur positive Werte.

• Ist $a$ negativ, hat die Funktion nur negative Werte. (Die Funktion wurde an der x-Achse gespiegelt.)

In dieser Aufgabe:

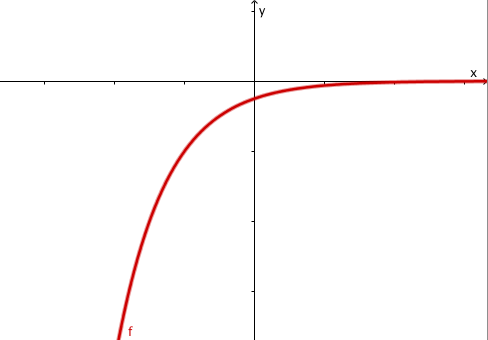
Die Funktionswerte nähern sich immer mehr an die x-Achse an $\Rightarrow 0<b<1$. Die Funktion hat nur negative Werte $\Rightarrow a<0$. Der richtige Term ist $-{1\over2}\cdot\left({1\over2}\right)^x$.