Aufgaben zu Exponentialfunktionen
Hier findest du Verständnis- und Rechenaufgaben rund um Exponentialfunktionen. Schaffst du sie alle?
- 1
Finde das exponentielle Wachstum
- 2
Wähle richtige Antworten aus.
Die Exponentialfunktion in ihrer einfachsten Form …
Betrachte die Exponentialfunktion mit . Also z.B. oder .
Gilt für die Funktion , dass beliebige Werte größer Null annehmen kann, dann…
Wenn die Exponentialfunktion in der allgemeinen Form gegeben ist und für und nur positive Werte eingesetzt werden, dann…
- 3
Erkenne Funktionsterme
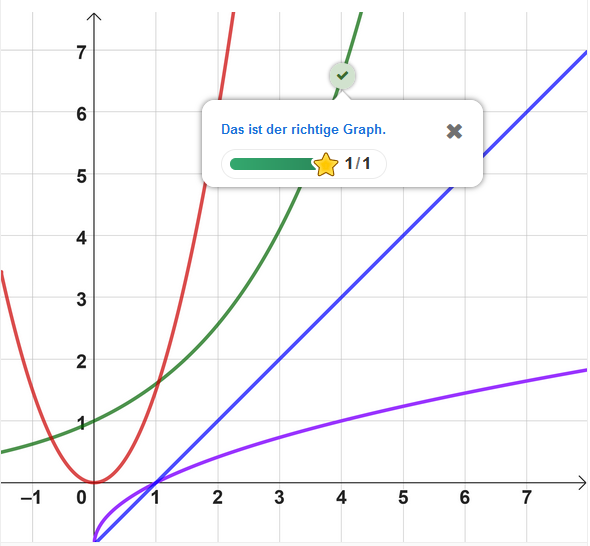
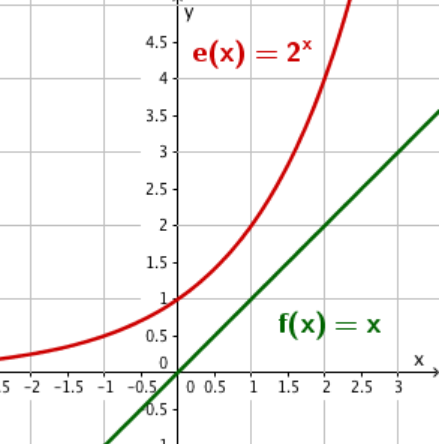
Welcher Funktionsterm gehört zum Graphen der gezeichneten Exponentialfunktion?
Welcher Funktionsterm passt?
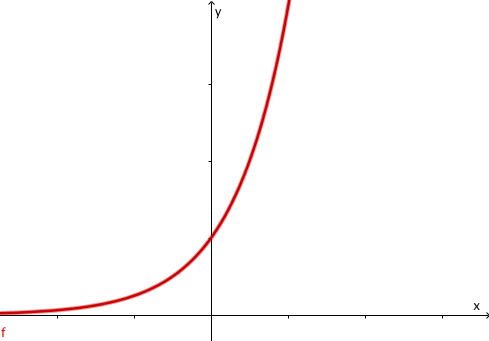
Welcher Funktionsterm passt?
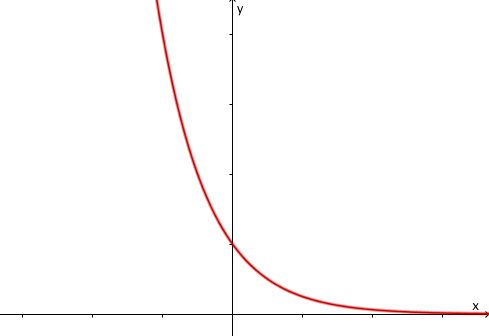
Welcher Funktionsterm passt?
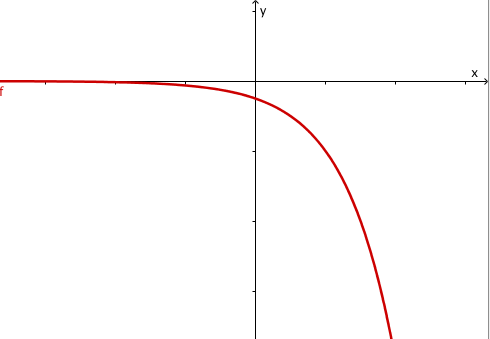
Welcher Funktionsterm passt?
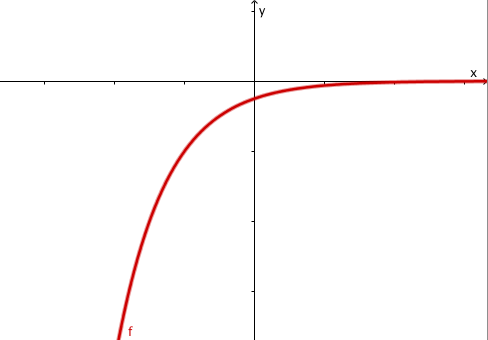
- 4
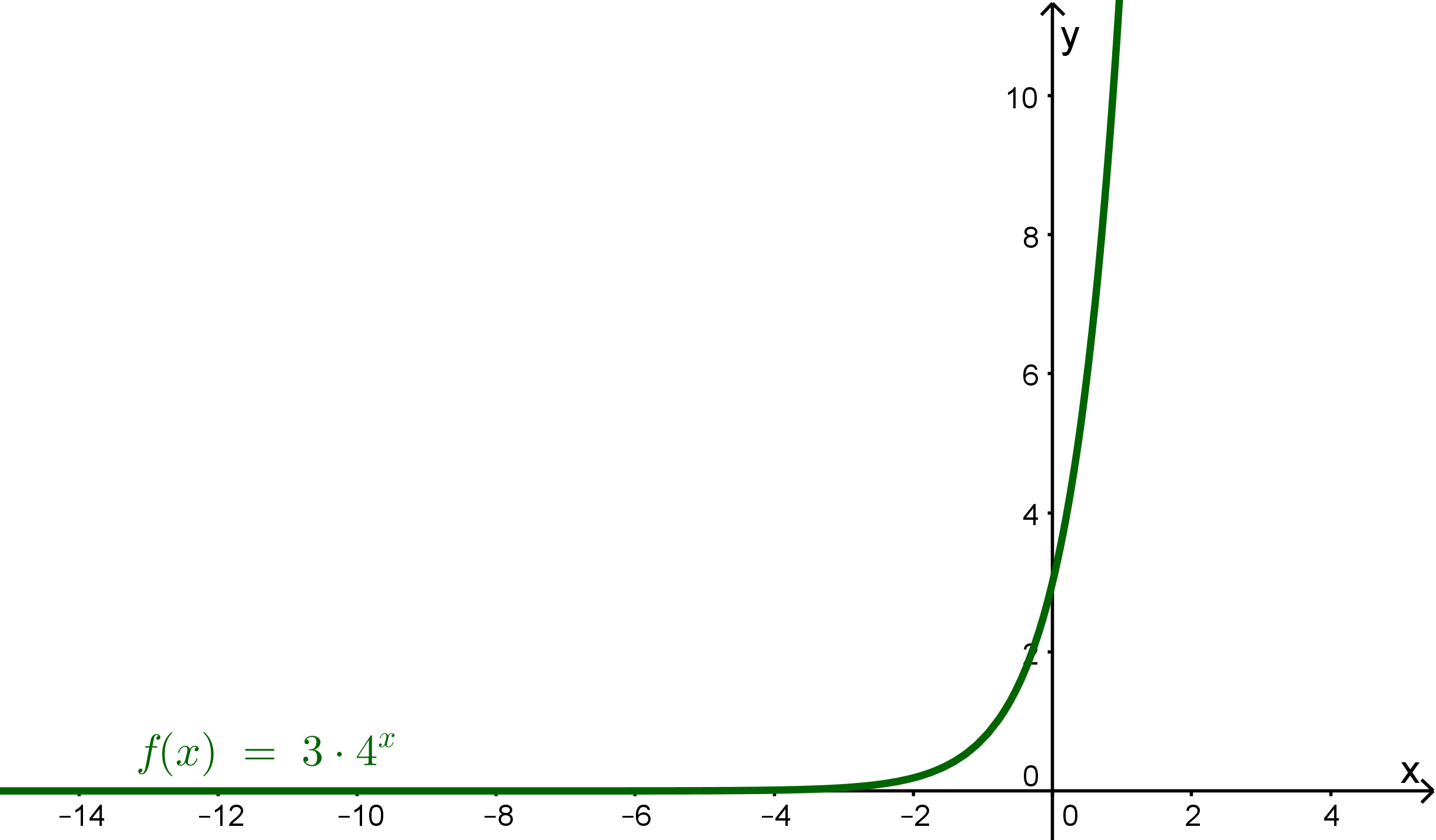
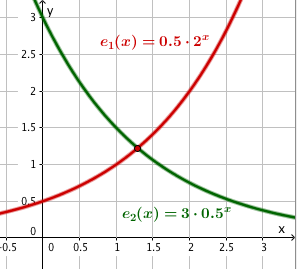
Welcher Graph gehört zum gegebenen Funktionsterm?
Welcher Graph gehört zu ?
Welcher Graph gehört zum Funktionsterm ?
Welcher Graph gehört zu ?
- 5
Beschreibe die Eigenschaften der Funktion und skizziere sie.
- 6
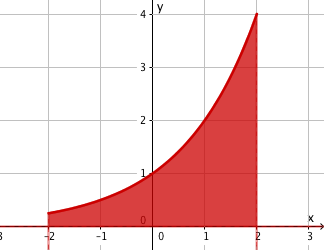
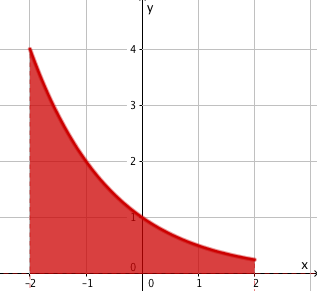
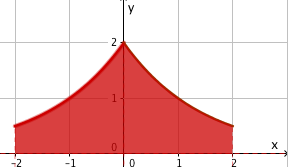
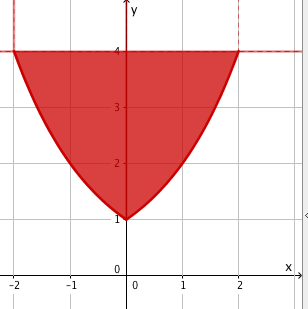
Schraffiere im Koordinatensystem alle Punkte P(x|y) im Bereich mit folgenden Vorgaben für den y-Wert
und
und
- 7
Bestimme - falls möglich - die Basis der Funktion so, dass ein gegebener Punkt P auf dem Graphen von liegt.
- 8
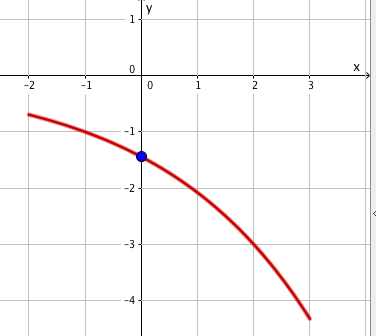
Die Punkte und sind Punkte des Graphen der Exponentialfunktion .
Skizziere den Graphen von für und lies daraus einen Näherungswert für den Parameter ab.
Berechne a und b.
- 9
Graphisches Lösen von Exponentialgleichungen
Einführungsbeispiel
Löse die Gleichung graphisch.
Lösung
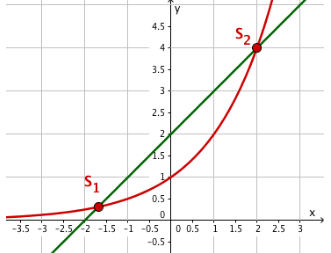
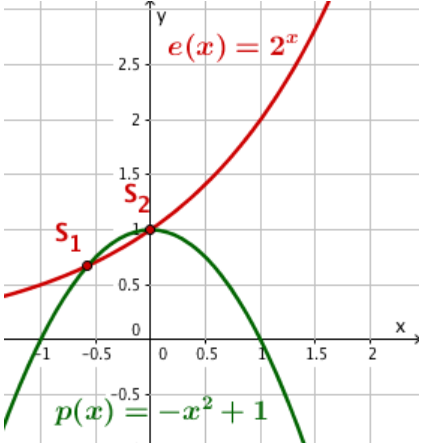
Zeichne den Graphen der Parabel und den der Exponentialfunktion .
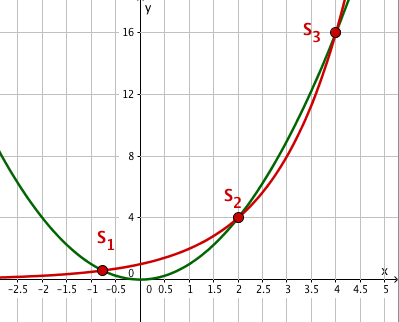
Die x-Koordinaten der gemeinsamen Punkte (Schnittpunkte) beider Graphen sind die gesuchten Lösungen der Gleichung .
Die ganzzahligen Lösungen und findet man natürlich auch durch Probieren. (eine irrationale Zahl) als Näherungswert nur graphisch.
Oft will man nur feststellen, ob eine Gleichung überhaupt lösbar ist, oder es reichen grobe Näherungswerte der Lösungen, dann genügen für die graphische Lösung Handskizzen der Graphen. Willst du es genauer, dann verwendest du einen Funktionsplotter zum Zeichen der Graphen.
Für die anschließenden Aufgaben sollen Handskizzen genügen.
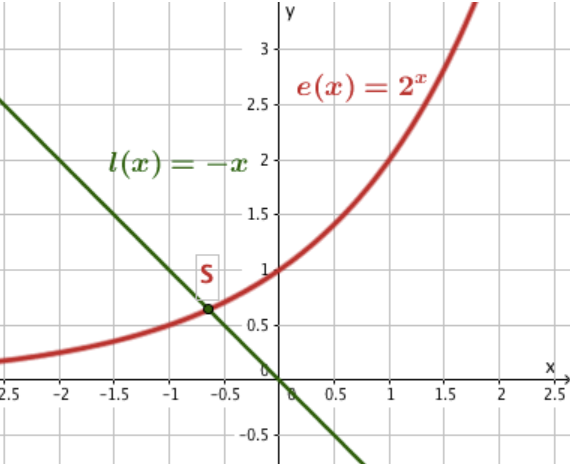
Löse die Exponentialgleichung graphisch.
Löse die Exponentialgleichung graphisch.
Löse die Exponentialgleichung graphisch.
Löse die Exponentialgleichung graphisch.
Löse die Exponentialgleichung graphisch und - falls du den Logarithmus schon kennst - auch rechnerisch.
- 10
Bringe Exponentialfunktionen auf die Grundform und entscheide dann, ob der Graph steigend oder fallend ist.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?