Bringe Exponentialfunktionen auf die Grundform und entscheide dann, ob der Graph steigend oder fallend ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
↓ Wende ein Potenzgesetz an und zerlege in ein Produkt.
↓ Rechne aus.
↓ Beachte dabei den negativen Exponenten!
↓ Vereinfache weiter.
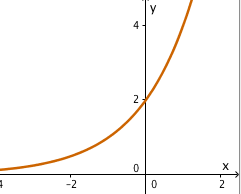
Basis und somit .
Vorfaktor und somit
⇒ Graph von steigend
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
↓ Zerlege den Potenzterm mit einer Potenzregel in ein Produkt.
↓ Rechne das Produkt soweit wie möglich aus.
Basis
Vorfaktor
Also ist der Graph von steigend
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
↓ Zerlege den Potenzterm mit einer Potenzregel in ein Produkt.
↓ Rechne negative Exponenten in positive um.
↓ Zerlege den Potenzterm erneut und berechne den Rest.
↓ Wähle die Basis nun so, dass sich insgesamt die Form ergibt.
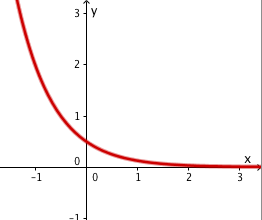
Basis
Vorfaktor
⇒ Graph von fallend
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
↓ Zerlege den Potenzterm mit einer Potenzregel.
↓ Zerlege den Potenzterm erneut.
↓ Wandle den negativen Exponenten in einen positiven um und berechne.
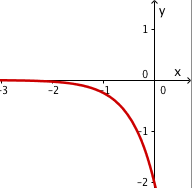
Basis
Vorfaktor
⇒ Graph von fallend.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

