Aufgaben zur Polynomdivision - lernen mit Serlo!

Zeige, dass die Polynomdivisionen dieser Aufgabengruppe nicht aufgehen. Gib für jede der zu den Polynomdivisionen gehörenden gebrochenrationalen Funktion deren asymptotisches Verhalten im Unendlichen an.

$(2 x^{2} - x - 2) : (x - 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\begin{array}{l} (2 x^{2} - x - 2) : (x - 1) = 2 x + 1 - \frac{1}{x - 1} \\ - (2 x^{2} - 2 x) \\ 1 x - 2 \\ - (1 x - 1) \\ - 1 R e s t \end{array}$
Die Polynomdivision "geht nicht auf". Der verbleibende Rest $(- 1)$ wird als Bruchterm mit dem Divisor als Nenner zum Teilergebnis des Divisionsverfahrens hinzugefügt.
Nun folgt die Asymptotenberechnung für $x \to \pm \infty$ .
Dem Quotient $(2 x^{2} - x - 2) : (x - 1)$ entspricht die gebrochenrationale Funktion
$f (x) = \frac{2 x^{2} - x - 2}{x - 1}$
Die Polynomdivision hat f(x) in die Differenz aus dem Polynom ersten Grades $a (x) = 2 x + 1$ und der echtgebrochenrationalen Funktion $r (x)$ zerlegt.
$f (x) = \underset{a (x)}{\underset{⏟}{2 x + 1}} - \underset{r (x)}{\underset{⏟}{\frac{1}{x - 1}}}$
Bringe $a (x)$ auf die linke Seite der Gleichung.
$f (x) - a (x) = \frac{- 1}{x - 1}$
Für jede echtgebrochenrationale Funktion $r (x)$ gilt:
$\lim_{x \to \pm \infty} r (x) = 0$
$f (x) - a (x) = \underset{\to 0 falls x \to \pm \infty}{\underset{⏟}{\frac{- 1}{x - 1}}}$
Damit unterscheiden sich $f (x)$ und $a (x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a (x) = 2 x + 1$ ist deshalb die Asymptote von $f (x)$ für $x$ gegen plus/minus Unendlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$(x^{2} - x) : (x + 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\begin{array}{l} (x^{2} - x) : (x + 1) = x - 2 + \frac{2}{x - 1} \\ - (x^{2} + x) \\ - 2 x + 0 \\ - (2 x - 2) \\ 2 R e s t \end{array}$
Die Polynomdivision "geht nicht auf". Der verbleibende Rest wird als Bruchterm mit dem Divisor als Nenner dem Teilergebnis hinzugefügt.
Nun folgt die Asymptotenberechnung für $x \to \pm \infty$ .
Dem Quotienten $(x^{2} - x) : (x + 1)$ entspricht die gebrochenrationale Funktion
$f (x) = \frac{x^{2} - x}{x + 1}$
Die Polynomdivision hat $f (x)$ in die Summe aus der linearen Funktion $a (x)$ und die echtgebrochenrationale Funktion $r (x)$ zerlegt.
$f (x) = \underset{a (x)}{\underset{⏟}{x - 2}} + \underset{r (x)}{\underset{⏟}{\frac{2}{x + 1}}}$
Bringe $a (x)$ auf die linke Seite der Gleichung.
$f (x) - a (x) = \frac{2}{x + 1}$
Für jede echtgebrochenrationale Funktion $r (x)$ gilt
$\lim_{x \to \pm \infty} r (x) = 0$
$f (x) - a (x) = \underset{\to 0 falls x \to \pm \infty}{\underset{⏟}{\frac{2}{x + 1}}}$
Damit unterscheidet sich $f (x)$ von $a (x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a (x) = x - 2$ ist somit die Asymptote von $f (x)$ für $x$ gegen plus/minus Unendlich.
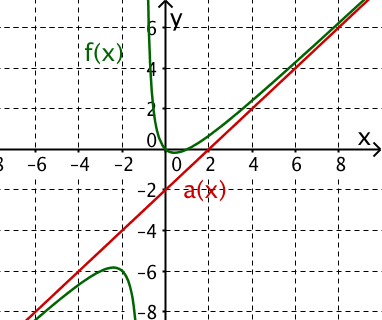
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$(x^{3} - 2 x^{2} + 1) : (2 x^{2} + 4 x)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
$\begin{array}{l} (x^{3} - 2 x^{2} + 1) : (2 x^{2} + 4 x) = \frac{1}{2} x - 2 + \frac{8 x + 1}{2 x^{2} + 4 x} \\ - (x^{3} + 2 x^{2}) \\ - 4 x^{2} + 1 \\ - (- 4 x^{2} - 8 x) \\ + 8 x + 1 R e s t p o l y n o m \end{array}$
Die Polynomdivision "geht nicht auf".
Der Grad des verbleibenden Restpolynoms des Dividenden ist kleiner als der Grad des Divisors und es wird als Bruchterm mit dem Divisor als Nenner zum Teilergebnis des Divisionsverfahrens hinzugefügt
Nun folgt die Asymptotenberechnung für $x \to \pm \infty$ .
Dem Quotienten $(x^{3} - 2 x^{2} + 1) : (2 x^{2} + 4 x)$ entspricht die gebrochenrationale Funktion
$f (x) = \frac{x^{3} - 2 x^{2} + 1}{2 x^{2} + 4 x}$
Die Polynomdivision hat $f (x)$ in die Summe der linearen Funktion $a (x)$ und eine echtgebrochenrationale Funktion $r (x)$ zerlegt.
$f (x) = \underset{a (x)}{\underset{⏟}{0,5 x - 2}} + \underset{r (x)}{\underset{⏟}{\frac{8 x + 1}{2 x^{2} + 4 x}}}$
Bringe $a (x)$ auf die linke Seite der Gleichung.
$f (x) - a (x) = \frac{8 x + 1}{2 x^{2} + 4 x}$
Für jede echtgebrochenrationale Funktion $r (x)$ gilt
$\lim_{x \to \pm \infty} r (x) = 0$
$f (x) - a (x) = \underset{\to 0 falls x \to \pm \infty}{\underset{⏟}{\frac{8 x + 1}{2 x^{2} + 4 x}}}$
Damit unterscheidet sich $f (x)$ von $a (x)$ für $x$ gegen plus/minus Unendlich um beliebig wenig.
Die Gerade $a (x) = 0,5 x - 2$ ist somit die Asymptote der Funktion $f (x)$ für $x$ gegen plus/minus Unendlich.
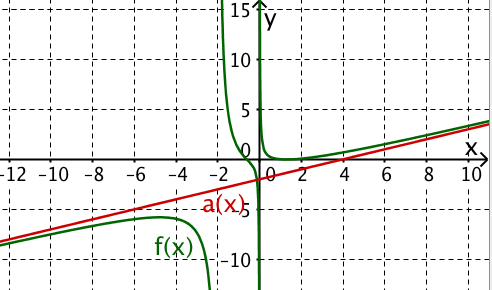
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$(1 - x^{4}) : (1 + x + x^{2})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Vorbereitung der Polynomdivision:
Ordne sowohl das Polynom des Dividenden als auch das Polynom des Divisors nach fallenden Potenzen.
$(1 - x^{4}) : (1 + x + x^{2}) =$
$(- x^{4} + 1) : (x^{2} + x + 1)$
Polynomdivision:
$\begin{array}{l} (- x^{4} + 1) : (x^{2} + x + 1) = - x^{2} + x + \frac{1 - x}{x^{2} + x + 1} \\ - (- x^{4} - x^{3} - x^{2}) \\ x^{3} + x^{2} + 1 \\ - (x^{3} + x^{2} + x) \\ - x + 1 R e s t \end{array}$
ausführliche Polynomdivision mit den fehlenden Gliedern im Dividenden
$\begin{array}{l} (- x^{4} + 0 \cdot x^{3} + 0 \cdot x^{2} + 0 \cdot x + 1) : (x^{2} + x + 1) = - x^{2} + x + \frac{1 - x}{x^{2} + x + 1} \\ - (- x^{4} - 1 \cdot x^{3} - 1 \cdot x^{2}) \\ + 1 \cdot x^{3} + 1 \cdot x^{2} + 0 \cdot x \\ - (x^{3} + x^{2} + x) \\ - x + 1 \end{array}$
Nun folgt die Asymptotenberechnung für $x \to \pm \infty$ .
Dem Quotienten $(- x^{4} + 1) : (x^{2} + x + 1)$ entspricht die gebrochenrationale Funktion
$f (x) = \frac{- x^{4} + 1}{x^{2} + x + 1}$
.
Die Polynomdivision hat $f (x)$ in die Summe aus dem Polynom 2. Grades $a (x) = - x^{2} + x$ und die echt gebrochenrationale Funktion r(x) mit dem Zählergrad 1 und dem Nennergrad 2 zerlegt.
$f (x) = \underset{a (x)}{\underset{⏟}{- x^{2} + x}} + \underset{r (x)}{\underset{⏟}{\frac{1 - x}{x^{2} + x + 1}}}$
Bringe $a (x)$ auf die linke Seite der Gleichung.
$f (x) - a (x) = \frac{1 - x}{x^{2} + x + 1}$
Für jede echtgebrochenrationale Funktion $r (x)$ gilt:
$\lim_{x \to \pm \infty} r (x) = 0$
$f (x) - a (x) = \underset{\to 0 falls x \to \pm \infty}{\underset{⏟}{\frac{1 - x}{x^{2} + x + 1}}}$
Damit unterscheiden sich $f (x)$ und $a (x)$ für x gegen plus/minus Unendlich um beliebig wenig.
Die nach unten geöffnete Parabel $a (x)$ ergibt die asymptotische Kurve von $f (x)$ für x gegen plus/minus Unendlich.
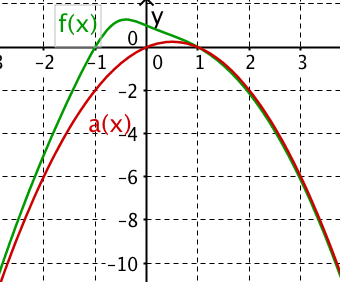
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?