Berechnung der Asymptote bei gebrochen-rationalen Funktionen

Für gebrochen-rationale Funktionen lässt sich einfach durch Vergleich der Grade von Zähler und Nenner bestimmen, ob diese Asymptoten im Unendlichen haben. Um diese konkret zu bestimmen, werden hier verschiedene Rechentechniken gezeigt. Eine allgemeine Definition der Asymptote findest Du im Artikel Asymptote.

Zunächst einmal vier Skizzen. An diesen kann man sich orientieren, um sich das Aussehen der Asymptoten grob vorzustellen.

Grobe Skizzen durch Vergleich der Grade

Es gibt vier Faustregeln, um sich eine grobe Vorstellung von dem Verlauf der Asymptote zu machen. Diese gelten egal welche gebrochenrationale Funktion man sich gerade anschaut.

Hinweis: Mit ZG oder NG ist jetzt immer der Grad des Zählers beziehungsweise der des Nenners gemeint.

1. ZG (Zählergrad) < NG (Nennergrad)

waagrechte Asymptote bei $y=0$

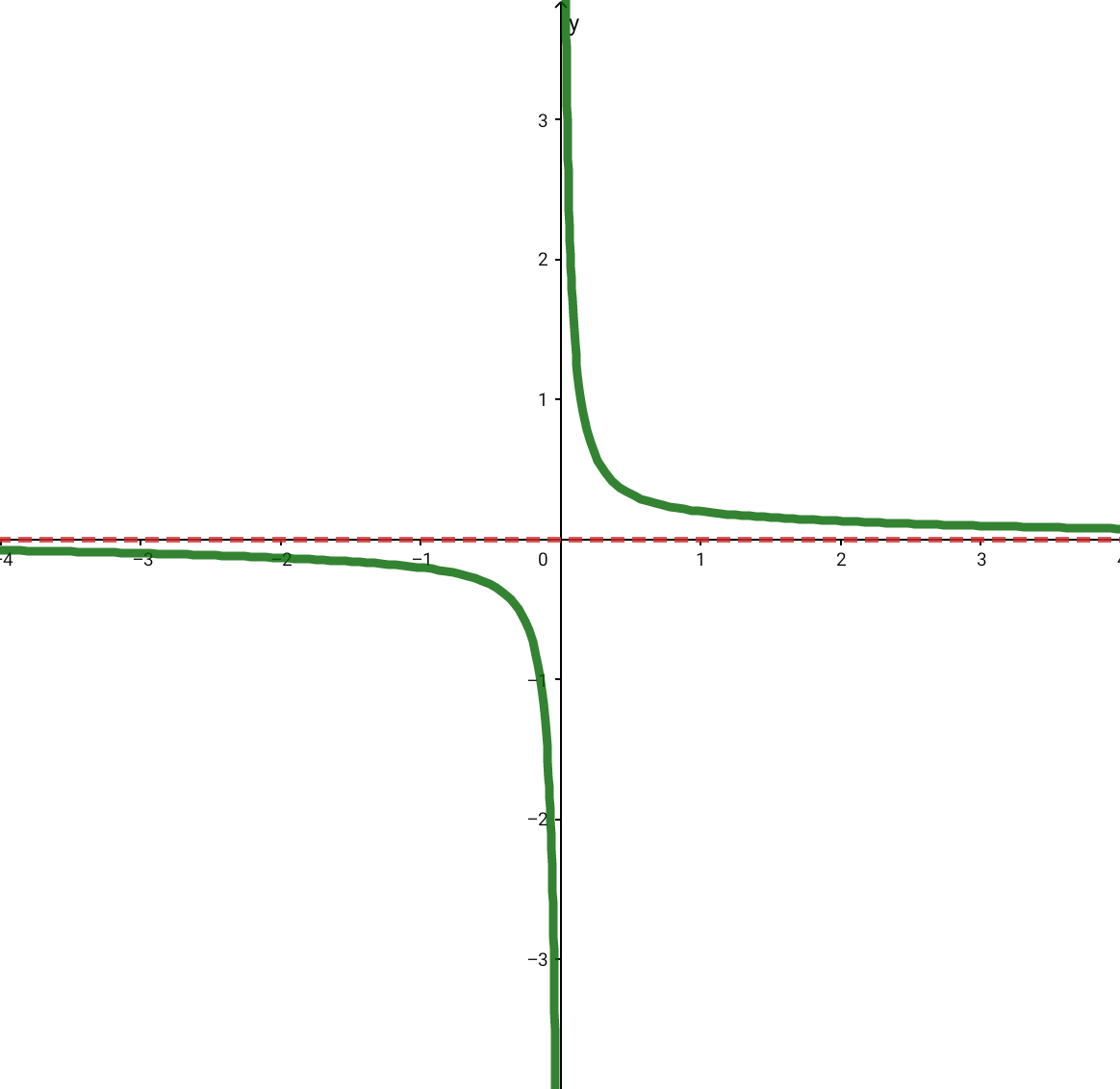
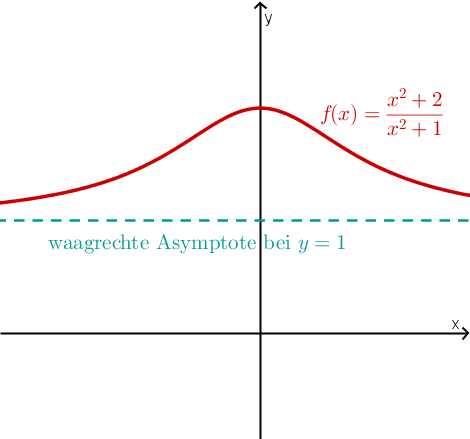
2. ZG (Zählergrad) = NG (Nennergrad)

waagrechte Asymptote bei einem $y$ - Wert $\neq 0$

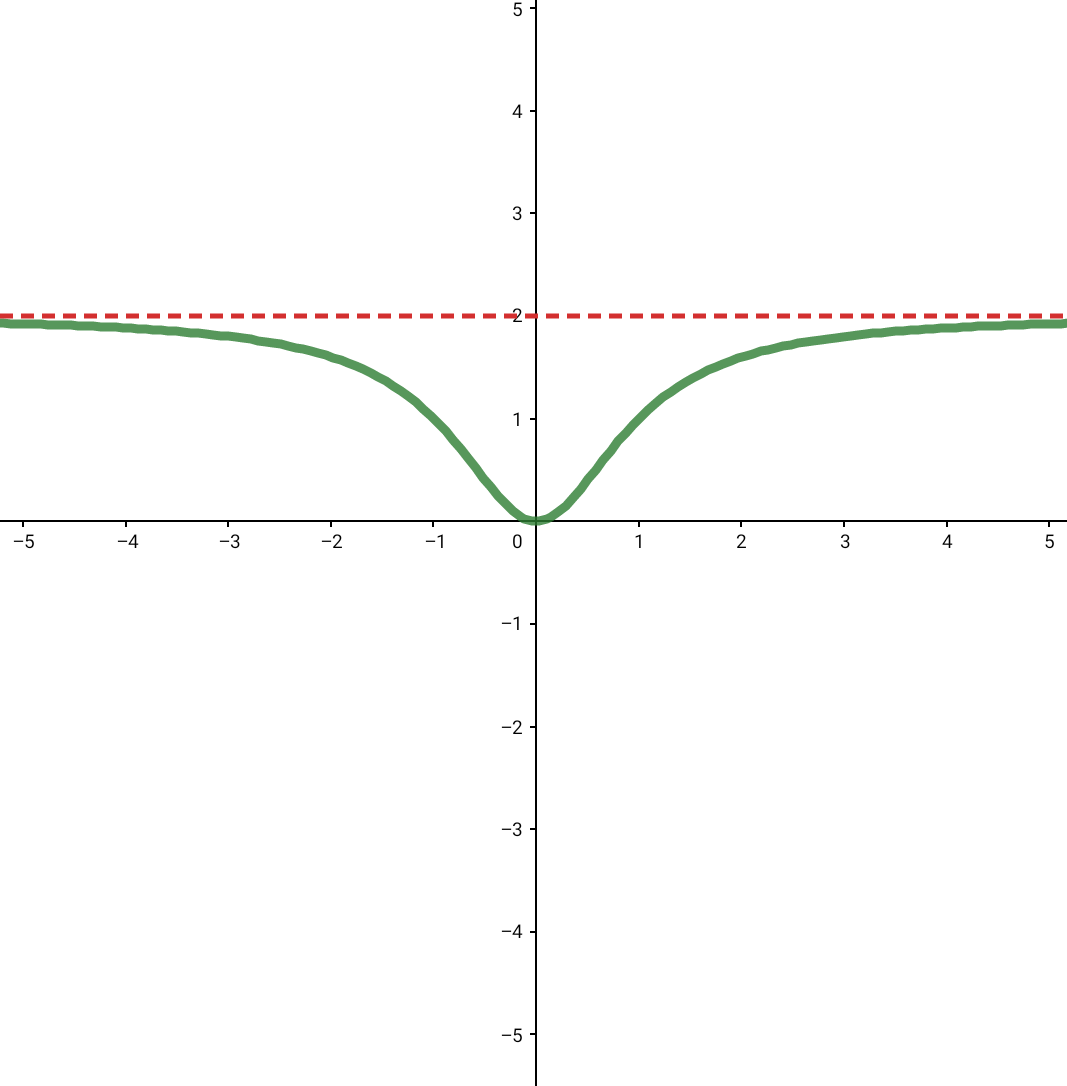
3. ZG (Zählergrad) = NG + 1 (Nennergrad)

schiefe Asymptote (Gerade)

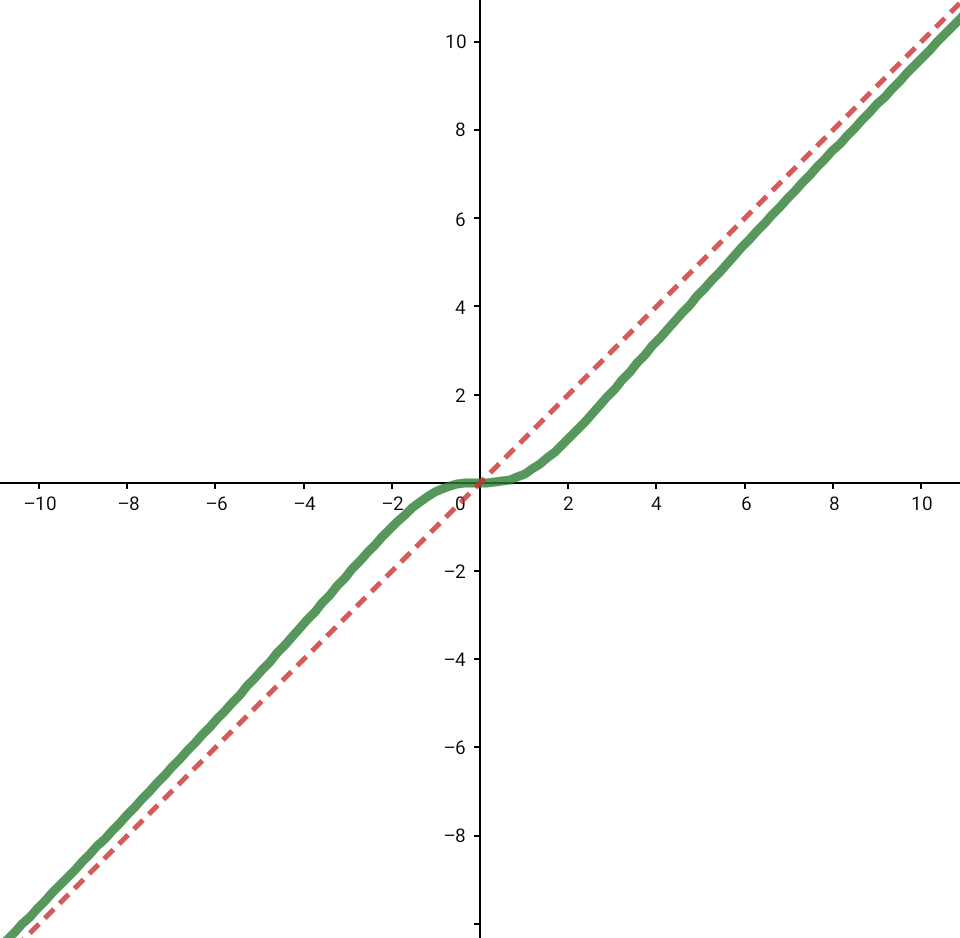
4. ZG (Zählergrad) > NG + 1 (Nennergrad)

kurvenförmige Asymptote

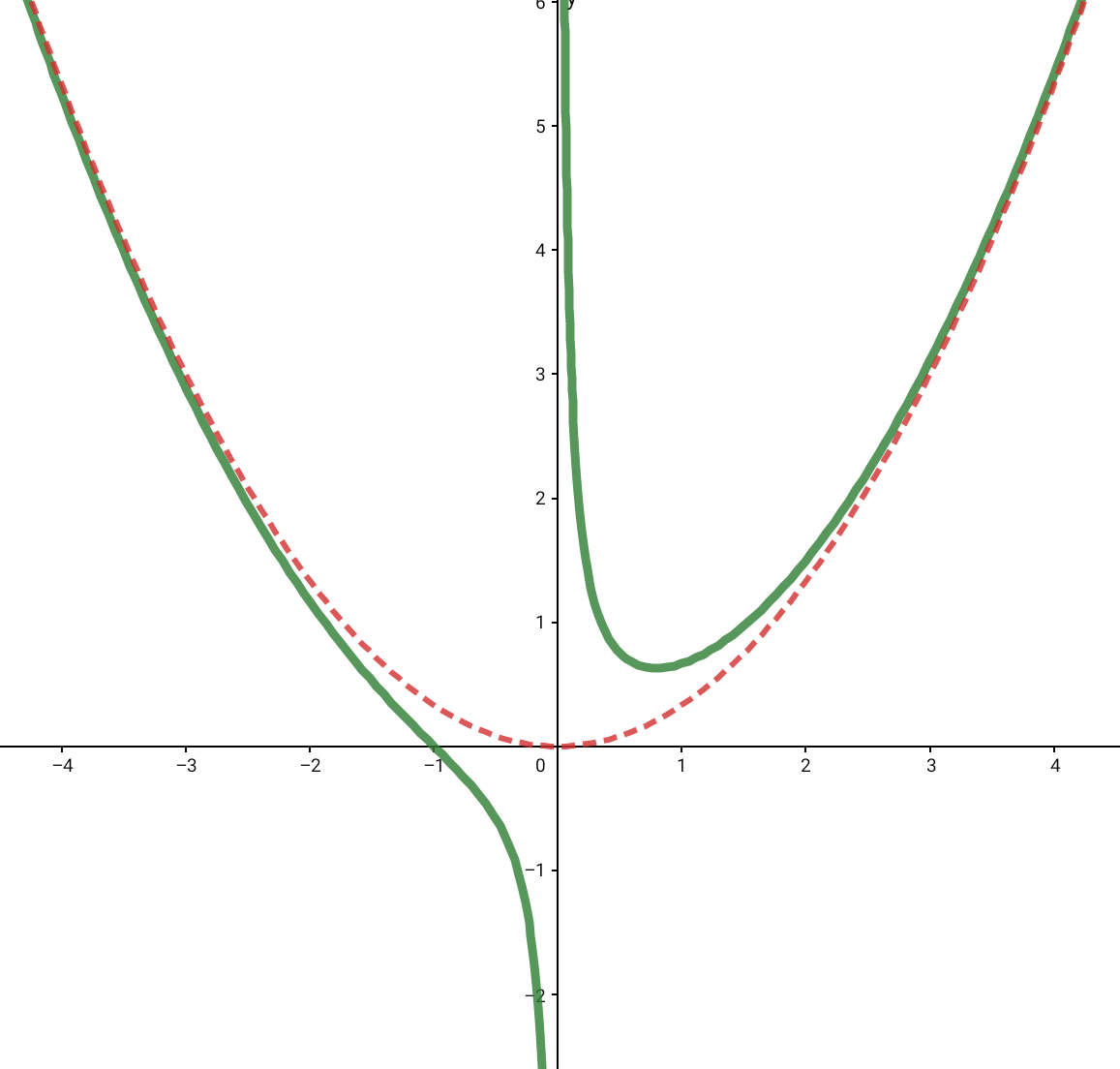
Asymptote Zählergrad größer Nennergrad + 1

Anmerkungen

Im zweiten Fall muss man die Funktion genauer untersuchen, um zu wissen, wo die waagerechte Asymptote liegt.
Diese Faustregeln gelten, auch wenn die Funktionen Polstellen haben. Die schwarz eingezeichneten Funktionen würden dann anders aussehen, aber der Verlauf der Asymptoten würde sich nicht groß ändern.
Im Fall ZG > NG lässt sich der Funktionsterm der Asymptote mithilfe von Polynomdivision bestimmen.
Senkrechte Asymptoten können bei Nullstellen des Nenners auftreten. Die Vielfachheit der Nullstelle bestimmt hierbei ggf., ob ein Vorzeichenwechsel auftritt.

Berechnung der Asymptote

Bei gebrochen-rationalen Funktionen betrachtet man zur Bestimmung der Asymptoten vor allem den Zähler- und Nennergrad (ZG und NG) und die Vielfachheit der Nullstellen in Zähler und Nenner.

Waagrechte Asymptoten

$\mathrm{ZG}<\mathrm{NG}:y=0$ ist Asymptote.

$\mathrm{ZG}=\mathrm{NG}$ : $y=\dfrac{a_n}{b_n}$ ist Asymptote, wobei $a_n$ der Koeffizient der höchsten Zählerpotenz und $b_n$ der Koeffizient der höchsten Nennerpotenz ist.

Senkrechte Asymptoten

Bei Polstellen betrachtet man die Nullstellen des Nenners nach dem Kürzen des Bruchs.

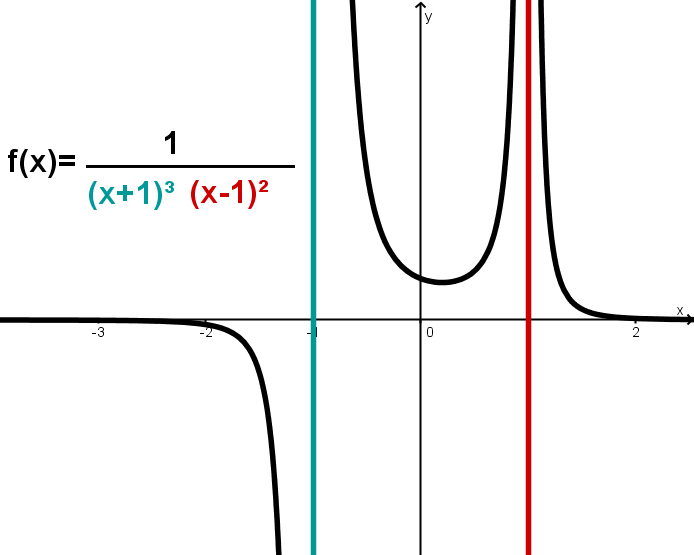
Vielfachheit der Nullstelle $x_0$ :

ungerade Vielfachheit $\Rightarrow$ senkrechte Asymptote bei $x_0$ mit Vorzeichenwechsel.

gerade Vielfachheit $\Rightarrow$ senkrechte Asymptote bei $x_0$ ohne Vorzeichenwechsel.

Um das Vorzeichen zu erhalten, betrachtet man den links- und rechtsseitigen Grenzwert.

Schiefe Asymptoten

ZG = NG+1 $\Rightarrow$ Es gibt eine schiefe Asymptote.

Die Geradengleichung der schiefen Asymptote erhält man durch Polynomdivision des Zählers durch den Nenner.

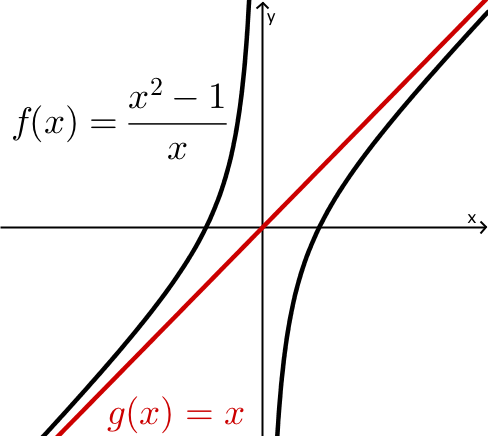
Beispiel

Man hat $f\left(x\right)=\dfrac{\left(x+0{,}5\right)^3}{x^2}$ gegeben und will anhand einer Betrachtung der Asymptoten den Graphen skizzieren.

Skizzieren: man sollte als allererstes grob einzeichnen, was man schon weiß.

Waagrechte Asymptoten

Mit der Grenzwertbetrachtung sieht man, dass es keine waagrechten Asymptoten gibt.

Senkrechte Asymptoten

Nenner $x^2$ hat die Nullstelle $0$ mit gerader Vielfachheit: zwei. $\Rightarrow\;\;$ Es gibt eine senkrechte Asymptote bei $0$ ohne Vorzeichenwechsel.

Setzt man einen Wert in den Funktionsterm ein, der geringfügig kleiner/größer als Null ist, erhält man das Vorzeichen der Funktion links/rechts der Null.

Man wählt zum Beispiel $x=1$ . Das geht ohne Probleme, da es zwischen $0$ und $1$ keine Nullstelle gibt. Man erhält

\displaystyle f\left(1\right)=\dfrac{\left(1+0{,}5\right)^3}{1^2}

Da sowohl Nenner als auch Zähler in diesem Term positiv sind, weiß man, dass dieser Bruch positiv ist (auch ohne ihn explizit auszurechnen).

$\Rightarrow\;\;$ Der Graph hat um die Null ein positives Vorzeichen.

Nun kann man den Funktionsgraphen mit seinen Asymptoten skizzieren.

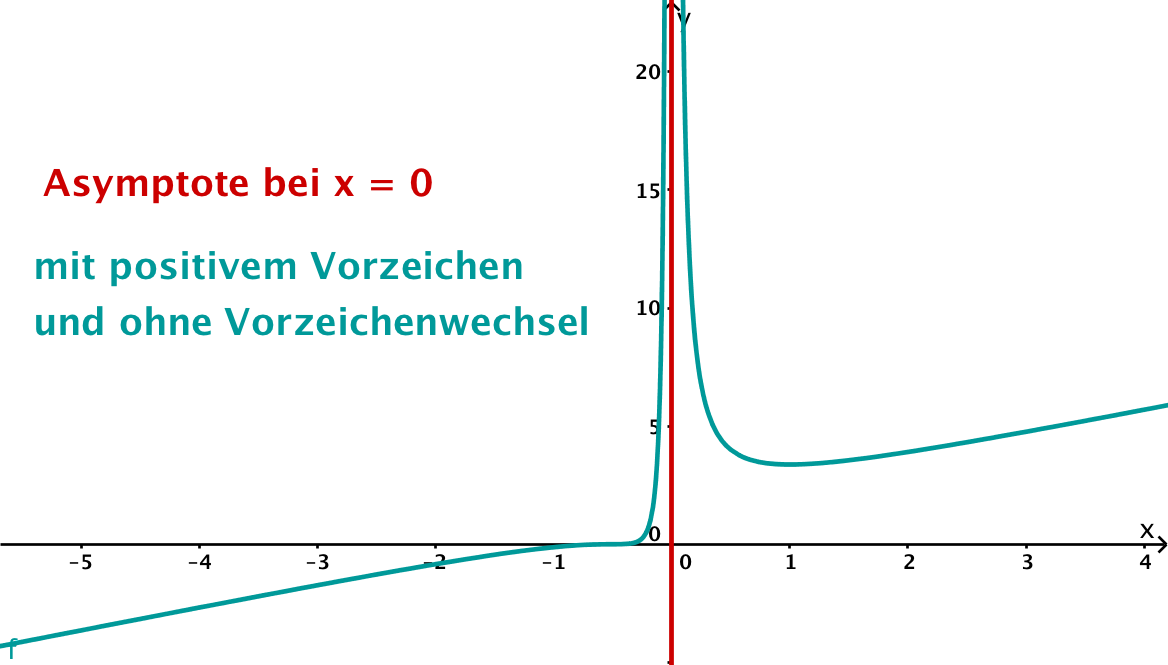
Schiefe Asymptoten

Um den Zähler- und Nennergrad zu erhalten, multipliziert man diese aus:

\displaystyle f\left(1\right)=\dfrac{\left(1+0{,}5\right)^3}{1^2}

$\Rightarrow\;\;$ ZG $=3=2+1=$ NG $+1$

$\Rightarrow\;\;$ Es gibt eine schiefe Asymptote.

Nun kannst du eine Polynomdivision durchführen. Alternativ lässt sich hier auch jeder Summand des Zählers durch den Nenner teilen:

$\def\arraystretch{2} \begin{array}{rcl}&&\left(x^3+1{,}5x^2+0{,}75x+0{,}125\right):x^2\\&=&\dfrac{x^3+1{,}5x^2+0{,}75x+0{,}125}{x^2}\\&=&\dfrac{x^3}{x^2}+\dfrac{1{,}5x^2}{x^2}+\dfrac{0{,}75x+0{,}125}{x^2}\\&=&x+1{,}5+\dfrac{0{,}75x+0{,}125}{x^2}\end{array}$

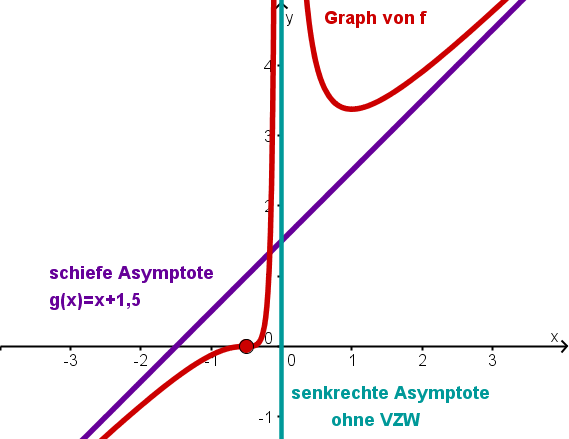
Der Nennergrad des Bruchs ganz rechts der Gleichung ist größer als der Zählergrad. Damit wird dieser Restterm für sehr große $x$ -Werte immer kleiner und nähert sich der $0$ an. Der Graph der gebrochenrationalen Funktion schmiegt sich deshalb dem Graphen der Asymptote mit der Gleichung $g(x)$ an:

\displaystyle f\left(1\right)=\dfrac{\left(1+0{,}5\right)^3}{1^2}

Ob der Graph der Funktion oberhalb oder unterhalb der Asymptote verläuft, hängt vom Vorzeichen des Restterms an der jeweiligen Stelle ab.

	$x\lt0{,}1\overline{6}$	$x=-0{,}1\overline6$	$x\gt -0{,}1\overline6$
Vorzeichen des Restterms	negativ	0	positiv
Lage der Funktionsgraphen	unterhalb der Asymptote	auf der Asymptote	oberhalb der Asymptote

Übungsaufgaben: Berechnung der Asymptote bei gebrochen-rationalen Funktionen

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Berechnen von Asymptoten

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Asymptote

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Berechnung der Asymptote bei gebrochen-rationalen Funktionen

Grobe Skizzen durch Vergleich der Grade

1. ZG (Zählergrad) < NG (Nennergrad)

2. ZG (Zählergrad) = NG (Nennergrad)

3. ZG (Zählergrad) = NG + 1 (Nennergrad)

4. ZG (Zählergrad) > NG + 1 (Nennergrad)

Anmerkungen

Berechnung der Asymptote

Waagrechte Asymptoten

Senkrechte Asymptoten

Vielfachheit der Nullstelle x0x_0x0​:

Schiefe Asymptoten

Beispiel

Waagrechte Asymptoten

Senkrechte Asymptoten

Schiefe Asymptoten

Übungsaufgaben: Berechnung der Asymptote bei gebrochen-rationalen Funktionen

Du hast noch nicht genug vom Thema?

Artikel

Vielfachheit der Nullstelle $x_0$ :