Rätselaufgaben zu besonderen ebenen Figuren

…

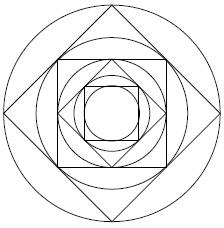
Folgende Figur besteht aus Quadraten und einbeschriebenen Kreisen.Wie ist das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreises?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras

Inkreis und Umkreis eines Quadrates

Man bertrachtet zunächst die zwei äußersten Kreise und das äußerste Quadrat.

Der Durchmesser des Inkreises im Quadrat ist $a$ , also gilt für den Innkreisradius: $r_{i} = \frac{a}{2}$

Kreis Quadrat Inkreis Umkreis Satz des Pythagoras legacy geogebra formula

Den Umkreisradius kann man mit Hilfe des Satz des Pythagoras berechnen:

$r_{u}^{2} + r_{u}^{2}$	$=$	$a^{2}$
$2 r_{u}^{2}$	$=$	$a^{2}$	$: 2$
$r_{u}^{2}$	$=$	$\frac{a^{2}}{2}$	$\sqrt{}$
	↓	Wurzel ziehen
$r_{u}$	$=$	$\sqrt{\frac{a^{2}}{2}}$
	$=$	$\frac{a}{\sqrt{2}}$
	↓	Bruch erweitern
	$=$	$\frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}$
	$=$	$\frac{a}{{(\sqrt{2})}^{2}} \cdot \sqrt{2}$
	$=$	$\frac{a}{2} \cdot \sqrt{2}$

Wir betrachten zuerst allgemein ein Quadrat mit Umkreisradius $r_{u}$ und Inkreisradius $r_{i}$ .

Löse die eben erhaltene Formel $r_{u} = \frac{a}{2} \cdot \sqrt{2}$ nach der Seitenlänge a auf:

$r_{u}$	$=$	$\frac{a}{2} \sqrt{2}$	$\cdot 2$
$2 r_{u}$	$=$	$a \sqrt{2}$	$: \sqrt{2}$
$a$	$=$	$\frac{2 r_{u}}{\sqrt{2}}$

Nun kann a in die Formel für den Inkreisradius $r_{i} = \frac{a}{2}$ eingesetzt werden:

$r_{i}$	$=$	$\frac{\frac{2 r_{u}}{\sqrt{2}}}{2}$
	↓	Faktor 2 kürzen
	$=$	$\frac{r_{u}}{\sqrt{2}}$

Das heißt $r_{i}$ ist $\frac{1}{\sqrt{2}} \approx 0,71$ so groß wie $r_{u}$ .

Weil diese Zusammenhang allgemein gilt, gilt er natürlich auch für das äußerste Quadrat. Also:

r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}

Nun betrachten wir das zweite Quadrat. Der Umkreis dieses Quadrats ist der Inkreis des äußersten Quadrats. Also gilt:

r_{i 1} = r_{u 2}

Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius erhalten wir:

r_{i 2} = \frac{r_{u 2}}{\sqrt{2}} = \frac{r_{i 1}}{\sqrt{2}}

Setze jetzt $r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}$ ein und vereinfache:

\begin{aligned} r_{i 2} & = \frac{\frac{r_{u 1}}{\sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \end{aligned}

Der Umkreis des dritten Quadrats ist der Inkreis des zweiten Quadrats. Also gilt:

r_{u 3} = r_{i 2} = \frac{r_{u 1}}{2}

Aber auch der allgemeine Zusammenhang zwischen In- und Umkreisradius glit in diesem Quadrat:

r_{i 3} = \frac{r_{u 3}}{\sqrt{2}}

Setze $r_{u 3} = \frac{r_{u 1}}{2}$ ein und vereinfache:

\begin{aligned} r_{i 3} & = \frac{\frac{r_{u 1}}{2}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \end{aligned}

Auch beim vierten Quadrat ist der Umkreis der Inkreis des dritten Quadrats. Damit ergibt sich:

r_{u 4} = r_{i 3} = \frac{r_{u 1}}{2 \sqrt{2}}

Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius folgt:

r_{i 4} = \frac{r_{u 4}}{\sqrt{2}}

Setze $r_{u 4} = \frac{r_{u 1}}{2 \sqrt{2}}$ ein und vereinfache:

\begin{aligned} r_{i 4} & = \frac{\frac{r_{u 1}}{2 \sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \cdot \sqrt{2} \cdot \sqrt{2}} \\ = \frac{r_{u 1}}{4} \end{aligned}

Das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreis beträgt also 1:4.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0

serlo.org CC BY-SA 4.0

→ Was bedeutet das?