Aufgaben zu Sinussatz und Kosinussatz

Hier findest du Rechenaufgaben zum Sinus- und Kosinussatz, mit denen du deren Anwendung lernst.

Berechne die (rot markierten) gesuchten Größen. Runde das Ergebnis auf zwei Nachkommastellen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kosinussatz
Gegeben: $a = 4$ $b = 6$ $γ = 67^{\circ}$
Gesucht: $c = ?$
Der gegebene Winkel ist von den beiden gegebenen Seiten eingeschlossen. Verwende deshalb den Kosinussatz.
$c^{2}$ $=$ $a^{2} + b^{2} - 2 a b \cdot \cos (γ)$
↓
Setze die gegebenen Werte ein.
$c^{2}$ $=$ $4^{2} + 6^{2} - 2 \cdot 4 \cdot 6 \cdot \cos (67^{\circ})$
↓
Rechne die rechte Seite zusammen.
$c^{2}$ $\approx$ $33,24$ $\sqrt{}$
↓
Ziehe die Wurzel. Runde auf 2 Nachkommastellen.
$c$ $\approx$ $5,77$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

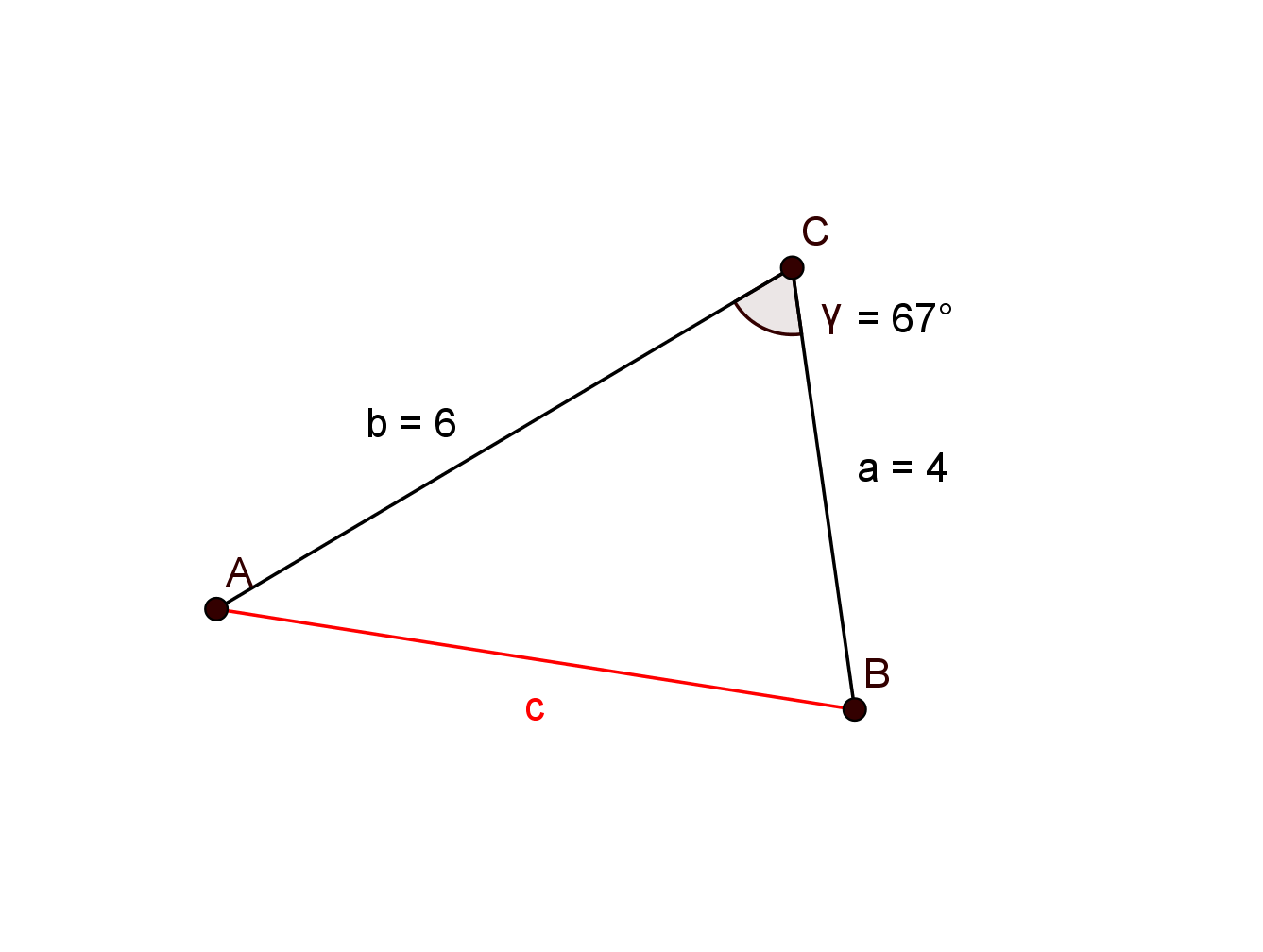
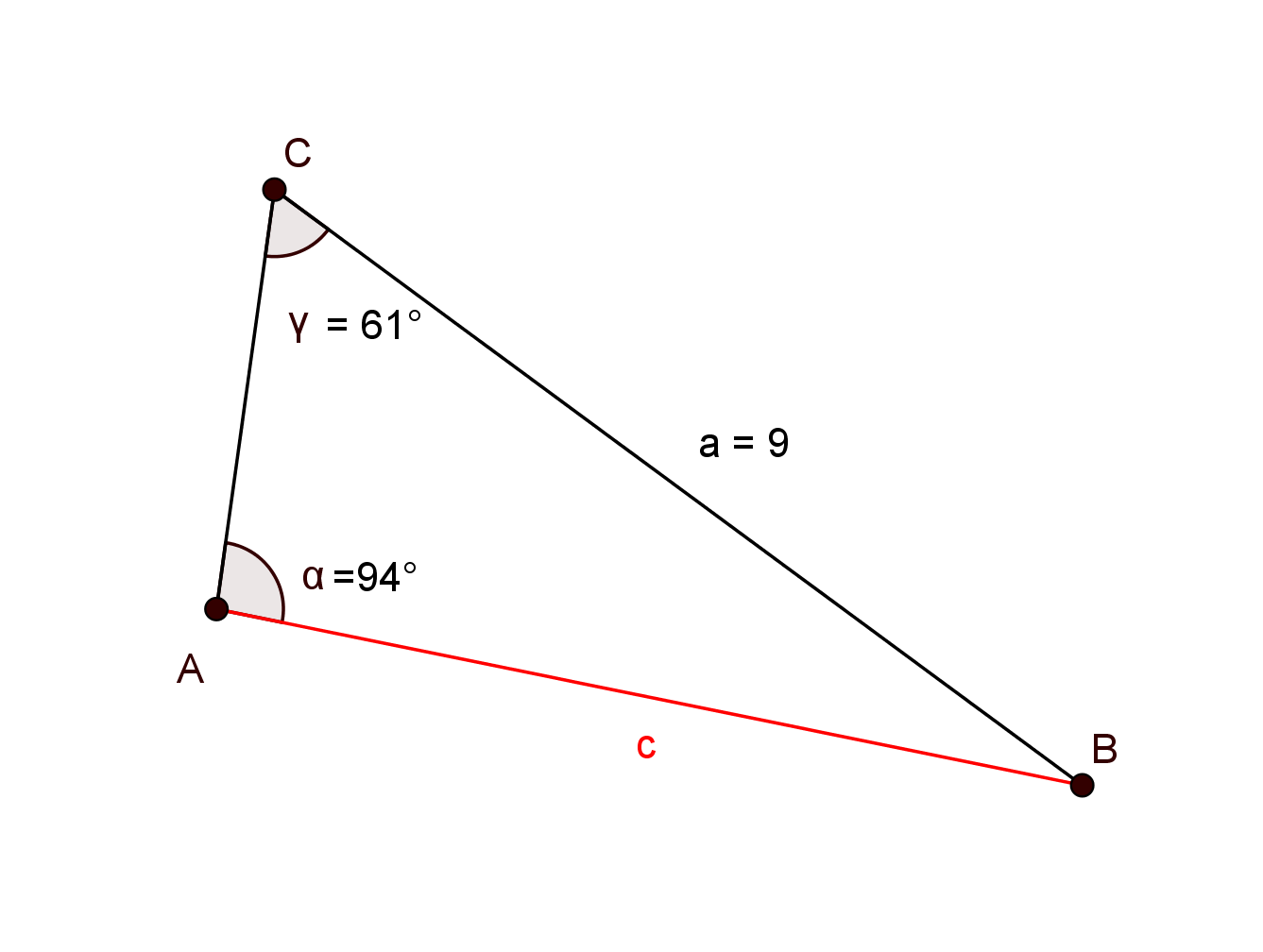
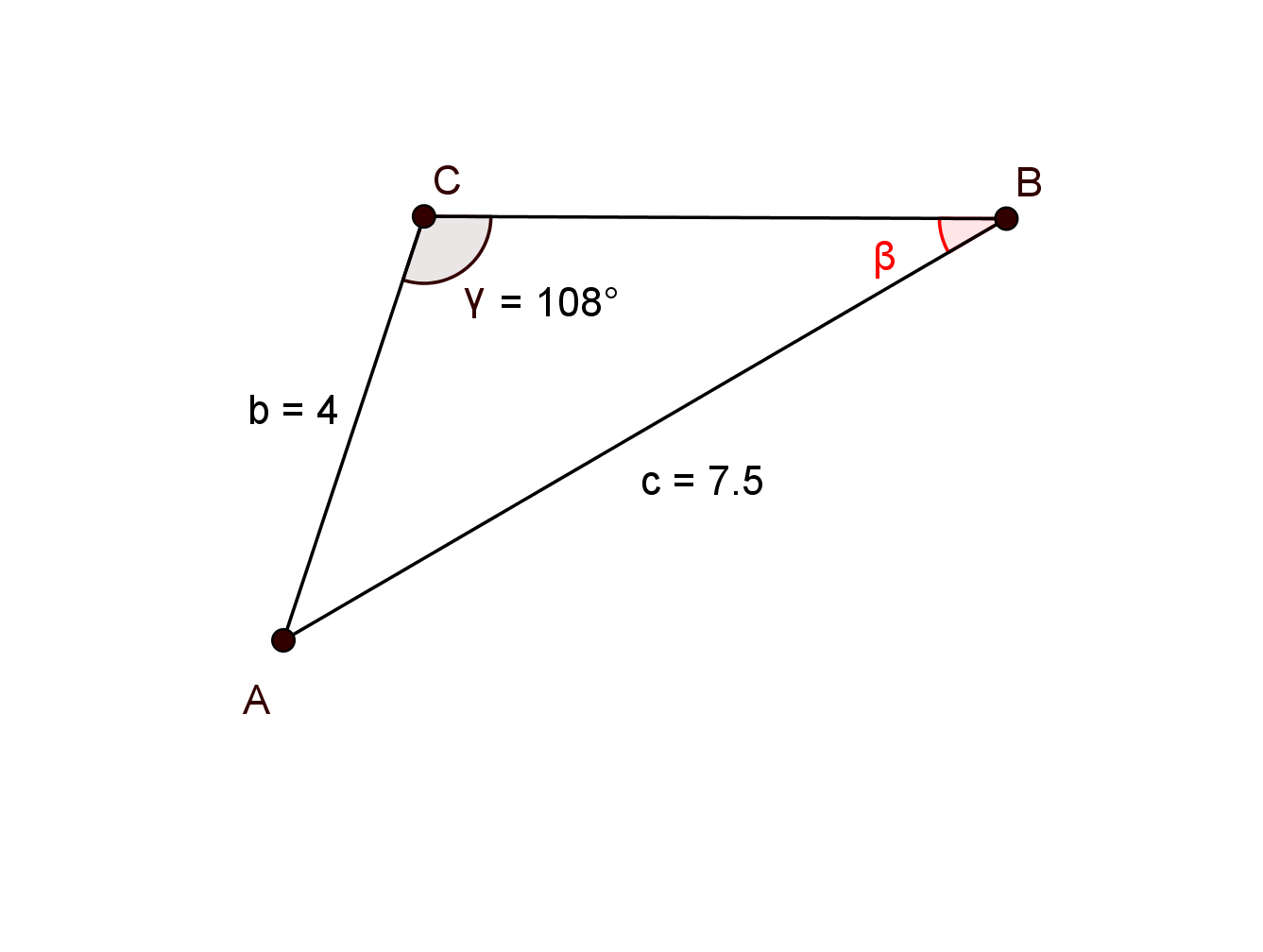2
Berechne die fehlenden Größen des Dreiecks, indem du den Kosinus- und Sinussatz anwendest.
Gegeben ist: $β = {36,1}^{\circ}$ ; $b = 9,5 cm$ und $γ = {111,5}^{\circ}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz
Berechne zuerst mit Hilfe des Sinussatzes die Länge der Seite c:
$\frac{b}{\sin (β)} = \frac{c}{\sin (γ)}$ Setze die bekannten Werte ein
$\frac{9,5}{\sin ({36,1}^{\circ})} = \frac{c}{\sin ({111,5}^{\circ})}$ Löse nach c auf.
$\Rightarrow c = \frac{9,5 \cdot \sin ({111,5}^{\circ})}{\sin ({36,1}^{\circ})} = 15,0$
Berechne nun mit Hilfe des Kosinussatzes die Länge der Seite $a$ :
$a = \sqrt{b^{2} + c^{2} - 2 b c \cdot \cos (α)}$
$= \sqrt{{9,5}^{2} + {15,0}^{2} - 2 \cdot 9,5 \cdot 15,0 \cdot \cos ({32,4}^{\circ})} = 8,6$
Der Winkel $α$ läßt sich berechnen aus:
180 $^{\circ}$ - ( $γ + β)$ = $180^{\circ} - ({111,5}^{\circ} + {36,1}^{\circ}) = 180^{\circ} - {147,6}^{\circ} = {32,4}^{\circ}$
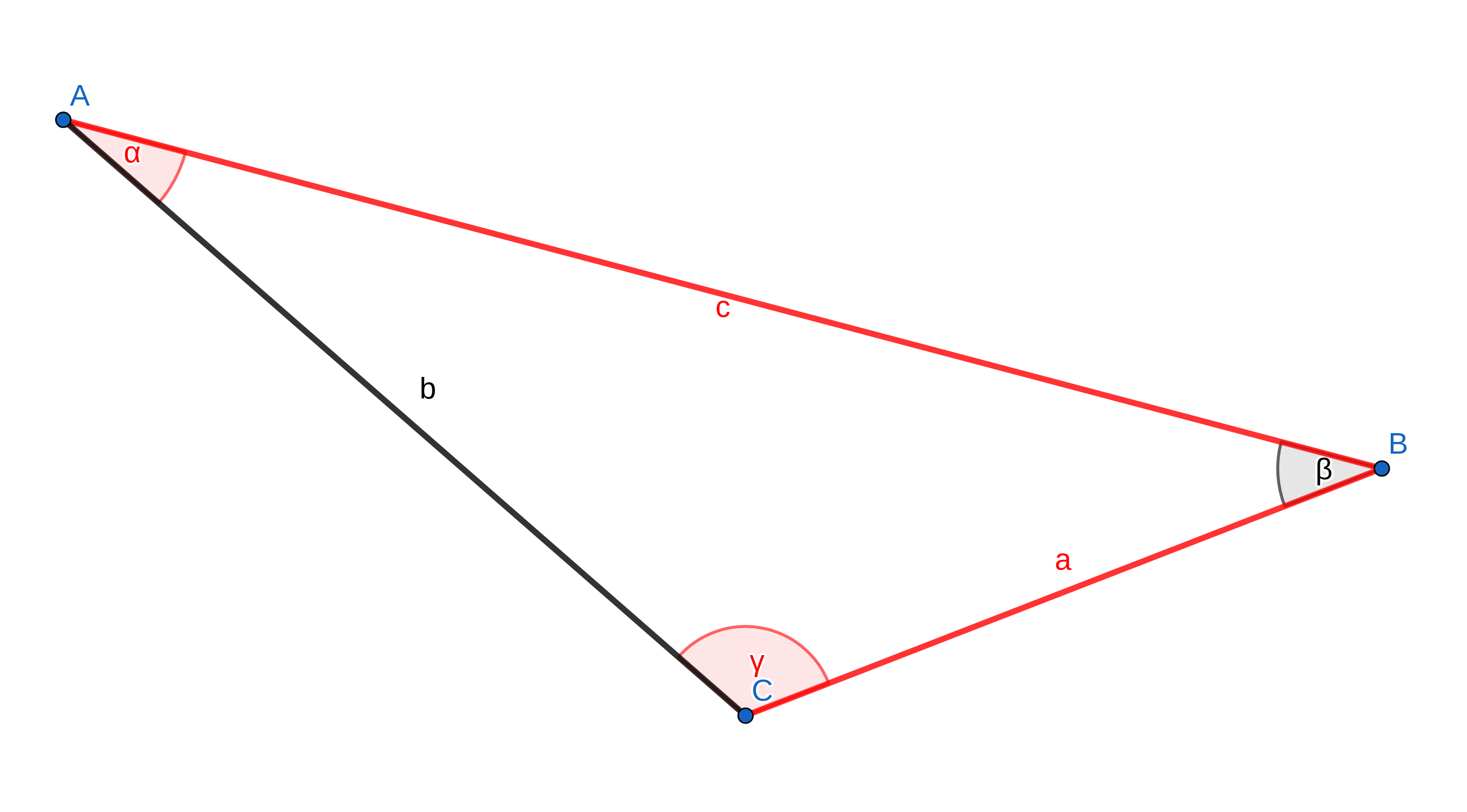
3
Die Skizze zeigt ein Parallelogramm mit den Seitenlängen: $a = 6 cm$ und $b = 8 cm$ und dem Winkel $α = 70^{\circ}$ .
Berechne den Winkel $ε$ .
°
Für diese Aufgabe benötigst Du folgendes Grundwissen: Eigenschaften eines Parallelogramms
Insbesondere benötigst du folgende Regeln:
Die Diagonalen in einem Parallelogramm halbieren sich.
Benachbarte Winkel ergänzen sich zu $180^{\circ}$ .
Zielgleichung aufstellen
Zunächst suchen wir eine Gleichung, die den gesuchten Winkel $ε$ enthält. Im Parallelogramm sind zunächst nur die Seitenlängen $a$ und $b$ sowie der Winkel $α$ bekannt. Da die Seite $a$ dem gesuchten Winkel gegenüberliegt, bietet sich der Kosinussatz für $a$ an.
Da sich in einem Parallelogramm die Diagonalen halbieren, haben die Seiten, die am Winkel $ε$ anliegen, die Länge $\frac{e}{2}$ bzw. $\frac{f}{2}$ . Die Zielgleichung ist also:
$a^{2} = {(\frac{e}{2})}^{2} + {(\frac{f}{2})}^{2} - 2 \cdot \frac{e}{2} \cdot \frac{f}{2} \cdot \cos (ε)$
Zielgleichung vereinfachen
Um später weniger rechnen zu müssen, kannst du die Gleichung durch Ausklammern und Kürzen vereinfachen:
$a^{2} = \frac{1}{4} (e^{2} + f^{2}) - \frac{e \cdot f}{2} \cdot \cos (ε)$
Fehlende Größen berechnen
Die Längen von $e$ und $f$ kannst du mit dem Kosinussatz berechnen. Es gilt:
$e^{2} = a^{2} + b^{2} - 2 a b \cos (α)$
$f^{2} = a^{2} + b^{2} - 2 a b \cos (β)$
In einem Parallelogramm ergänzen sich benachbarte Winkel zu $180 °$ . Also ist $β = 180 ° - α$ . Zusammen mit den Supplementbeziehungen für Sinus und Kosinus gilt:
$\cos (β) = \cos (180 ° - α) = - \cos (α)$
Damit berechnest du die Werte von $e^{2}, f^{2}$ bzw. $e, f$ :
$\begin{array}{lr} e^{2} = 100 - 96 \cdot \cos (α) \approx 67,17; & e \approx 8,20 \\ f^{2} = 100 + 96 \cdot \cos (α) \approx 132,83; & f \approx 11,53 \end{array}$
Einsetzen in die Zielgleichung
Einsetzen in die Zielgleichung $a^{2} = \frac{1}{4} (e^{2} + f^{2}) - \frac{e \cdot f}{2} \cdot \cos (ε)$ ergibt:
$\begin{array}{lrcll} 36 & \approx & 50 - 47,273 \cos (ε) & | - 50 \\ \Leftrightarrow & - 14 & \approx & - 47,273 \cos (ε) & | : (- 47,273) \\ \Leftrightarrow & \cos (ε) & \approx & 0,2962 \\ \Leftrightarrow & ε & \approx & 72,77 ° \end{array}$
Der gesuchte Winkel $ε$ hat die Größe $72,77 °$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\frac{b}{\sin (β)}$	$=$	$\frac{c}{\sin (γ)}$
	↓	Tipp: Indem du von beiden Brüchen den Kehrbruch bildest, kannst du die gesuchte Größe in den Zähler bekommen.
$\frac{\sin (β)}{b}$	$=$	$\frac{\sin (γ)}{c}$	$\cdot b$
	↓	Löse nach der gesuchten Größe auf.
$\sin (β)$	$=$	$\frac{\sin (γ)}{c} \cdot b$
	↓	Setze die gegebenen Werte ein.
$\sin (β)$	$=$	$\frac{\sin (108^{\circ})}{7,5} \cdot 4$
	↓	Rechne aus.
$\sin (β)$	$\approx$	$0,5072$	$\sin^{- 1}$
	↓	Löse nach dem Winkel auf.
$β$	$\approx$	$30, 48 °$

$b^{2}$	$=$	$a^{2} + c^{2} - 2 a c \cdot \cos (β)$	$- a^{2} - c^{2}$
	↓	Forme nach $β$ um.
$b^{2} - a^{2} - c^{2}$	$=$	$- 2 a c \cdot \cos (β)$	$: (- 2 a c)$
$\frac{b^{2} - a^{2} - c^{2}}{- 2 a c}$	$=$	$\cos (β)$	$\cos^{- 1}$
$β$	$=$	$\cos^{- 1} (\frac{b^{2} - a^{2} - c^{2}}{- 2 a c})$
	↓	Setze die gegebenen Werte ein.
$β$	$=$	$\cos^{- 1} (\frac{8^{2} - {5,1}^{2} - {4,3}^{2}}{- 2 \cdot 5,1 \cdot 4,3})$
	↓	Rechne aus und runde auf 2 Nachkommastellen.
$β$	$\approx$	$116,40 °$

$c^{2}$	$=$	$a^{2} + b^{2} - 2 a b \cdot \cos (γ)$
	↓	Setze die gegebenen Werte ein.
$c^{2}$	$=$	$4^{2} + 6^{2} - 2 \cdot 4 \cdot 6 \cdot \cos (67^{\circ})$
	↓	Rechne die rechte Seite zusammen.
$c^{2}$	$\approx$	$33,24$	$\sqrt{}$
	↓	Ziehe die Wurzel. Runde auf 2 Nachkommastellen.
$c$	$\approx$	$5,77$

$\frac{c}{\sin (γ)}$	$=$	$\frac{a}{\sin (α)}$	$\cdot \sin (γ)$
	↓	Forme nach der gesuchten Größe um. Multipliziere hierzu mit $\sin (γ)$ .
$c$	$=$	$\frac{a}{\sin (α)} \cdot \sin (γ)$
	↓	Setze die Werte ein.
$c$	$=$	$\frac{9}{\sin (94^{\circ})} \cdot \sin (61^{\circ})$
$c$	$\approx$	$7,89$

Aufgaben zu Sinussatz und Kosinussatz

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Zielgleichung aufstellen

Zielgleichung vereinfachen

Fehlende Größen berechnen

Einsetzen in die Zielgleichung