Gruppe A - lernen mit Serlo!

…

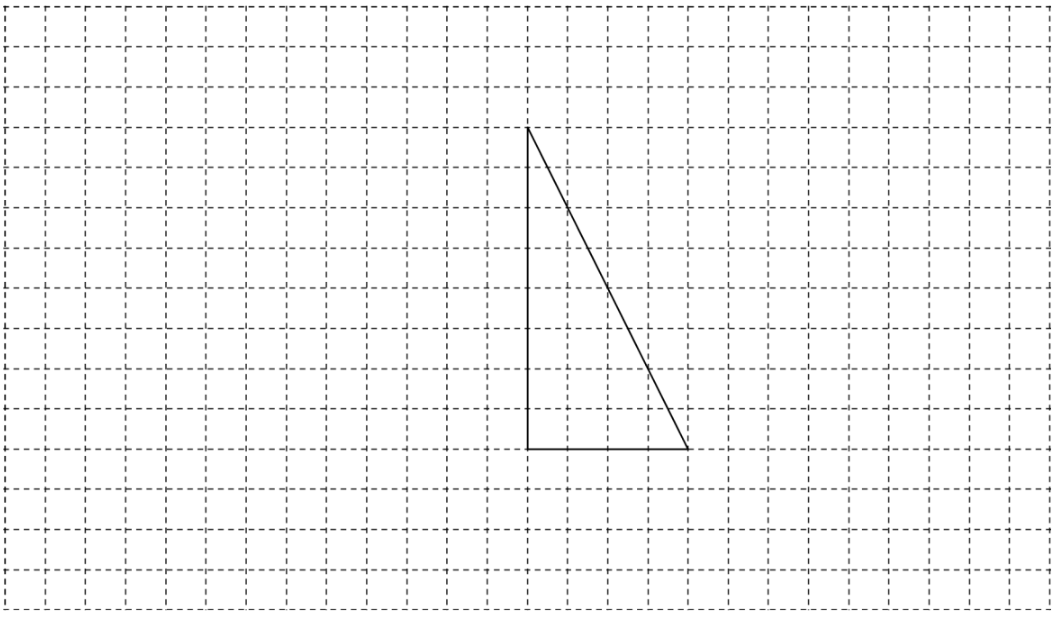
Ergänze das im Gitternetz abgebildete Dreieck so zu einer achsensymmetrischen Figur, dass der Inhalt des Dreiecks $\frac{2}{5}$ des Inhalts der Gesamtfläche der Figur beträgt. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsensymmetrie

In dieser Aufgabe sollst du das angegebene Dreieck so erweitern, dass

es achsensymmetrisch ist und
die Fläche des Dreiecks $\frac{2}{5}$ des Flächeninhalts der gesamten Figur ausmacht.

Bestimmung des Flächeninhalts der Gesamtfigur

Durch Abzählen der Kästchen kannst du den Flächeninhalt des Dreiecks berechnen:

A_{Δ} = \frac{1}{2} \cdot 4 \cdot 8 = 16

Da der Flächeninhalt des Dreiecks $A_{Δ}$ $\frac{2}{5}$ des Flächeninhalts der gesamten Fläche sein soll, kannst du nun den Flächeninhalt der gesamten Figur $A$ bestimmen.

$A_{Δ}$	$=$	$\frac{2}{5} \cdot A$	$\cdot \frac{5}{2}$
$\frac{5}{2} \cdot A_{Δ}$	$=$	$A$
	↓	Setze $A_{Δ} = 16$ ein.
$\frac{5}{2} \cdot 16$	$=$	$A$
$A$	$=$	$40$

Die Gesamtfigur muss also einen Flächeninhalt von 40 Kästchen haben. Du kannst nun auf vielen verschiedenen Arten das Dreieck zu einer achsensymmetrischen Figur mit diesem Flächeninhalt ergänzen.

Verschiedene Lösungsmöglichkeiten

Du kannst beispielsweise das Dreieck erstmal zu einem Rechteck ergänzen. Rechtecke sind achsensymmetrisch. Dieses entstandene Rechteck hat einen Flächeninhalt von $2 \cdot 16 = 32$ Kästchen. Jetzt können wir das Rechteck nach oben/unten oder links/rechts erweitern, um die fehlenden $8$ Kästchen Flächeninhalt zu ergänzen.

Deine Lösung kann dann so aussehen:

Eine andere Herangehensweise ist, den Flächeninhalt erstmal um $4$ Kästchen zu erweitern und die enstandene Figur zu spiegeln. Dann kann deine Lösung so aussehen:

Viele weitere Lösungen sind möglich! Du liegst immer richtig, wenn deine Gesamtfigur einen Flächeninhalt von 40 Kästchen hat und achsensymmetrisch ist.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0

serlo.org CC BY-SA 4.0

→ Was bedeutet das?