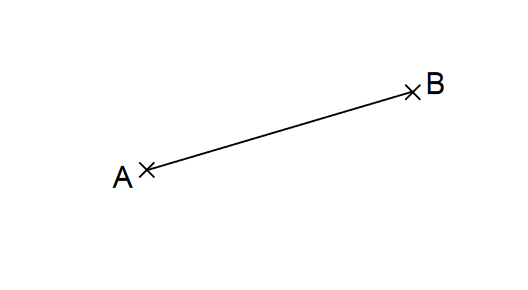
Die Abbildung zeigt die Hypotenuse eines rechtwinkligen Dreiecks ABC. Konstruiere den Punkt C so, dass die Kathete [AC] halb so lang ist wie die Hypotenuse. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Mittelsenkrechte
1.Zeichne einen Kreis um A, dessen Radius größer ist als der halbe Abstand zwischen A und B.
2. Nun Zeichne ebenfalls einen Kreis mit dem gleichen Radius um B.
3. Als nächstes wird die Mittelsenkrechte g eingezeichnet. Sie entsteht, wenn man eine Gerade durch die beiden Schnittpunkte der Kreise zeichnet.
4. Der Schnittpunkt der Strecke AB und der Mittelsenkrechten ergibt einen Punkt (I). Nun benutzen wir den Satz des Thales, damit unser Dreieck rechtwinklig wird. Das heißt es wird ein Kreis um I mit dem Radius AI gezogen.
5. Da die Strecke AC halb so lang sein soll wie die Strecke AB, wird ein Kreis um A gezogen, welcher den Radius AI hat (mit Hilfe der Mittelsenkrechten hatten wir den Mittelpunkt der Strecke AB ermittelt, somit ist I der Mittelpunkt der Strecke). Der Schnittpunkt ergibt den Punkt C.
6. Zu guter Letzt werden die Punkte A, B und C verbunden. Nun haben wir ein rechtwinkliges Dreieck, wo die Seite AC halb so lang ist wie die vorgegebene Strecke AB.
