Gruppe A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Ein Internetportal bietet Zusatzprogramme für Smartphones an. Bei jedem Verkauf eines solchen Programms behält der Betreiber des Portals $30\%$ des Verkaufpreises; den Rest erhält der Entwickler des Programms. Ein Entwickler eines Programms möchte bei jedem Verkauf 1,40 Euro erhalten. Ermittle den festzulegenden Kaufpreis. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Dreisatz
Beim Verkauf eines Programmes behält der Betreiber $30\%$ des Verkaufspreises,den Rest erhält der Entwickler.
Das heißt, der Entwickler erhält $70\%$ des Verkaufspreises. Der Entwickler möchte pro verkauftem Programm $1{,}40€$ verdienen. Der Kaufpreis berechnet sich daher wie folgt.
$1{,}40$ € $\widehat{=}$ $70\% \qquad \vert :7$
$0{,}20$ € $\widehat{=}$ $10 \% \qquad \vert\cdot10$
$2{,}00$ € $\widehat{=}$ $100\%$
Wenn der Entwickler $1{,}40 €$ und der Betreiber $30$ % pro Programm erhalten wollen, muss der Verkaufspreis $2{,}00€$ betragen.
2
Entscheide für jede der folgenden Aussagen, ob sie falsch oder wahr ist. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruenzsätze
Richtige Aussage (SWS-Satz):
Zwei Dreiecke sind kongruent, wenn sie in den Längen zweierSeiten und der Größe des eingeschlossenen Winkels übereinstimmen.
Falsche Aussage:
Alle Dreiecke, die in den Größen ihrer 3 Winkel übereinstimmen, sind kongruent.
3
Die Altstadt von Bamberg hat sowohl in Nord-Süd-Richtung als auch in Ost-West-Richtung eine Ausdehnung von etwa 1,8 km. In einer Informationsbroschüre soll die Altstadt auf einer Seite mit einer Breite von 10,5 cm und einer Länge von 14,5 cm vollständig abgebildet werden. Ermittle, ob sich der Maßstab 1:10.000 eignet. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Maßstab
Umrechnen der Längen
Zunächst musst du die in der Aufgabe gegebenen Längen in eine einheitliche Einheit umrechnen. Dazu brauchst du Grundwissen über das Umrechnen von Einheiten.
Da die Breite der Informationsbroschüre in $\text{cm}$ angegeben ist, musst du die Ausdehnung der Stadt von $\text{km}$ in $\text{cm}$ umrechnen.
$1\text{\,km}=1000\text{\,m}\Rightarrow 1{,}8\text{\,km}=1{,}8\cdot1000\text{\,m}=1800\text{\,m}$
$1\text{\,m}=100\text{\,cm}\Rightarrow 1800\text{\,m}=1800\cdot100\text{\,cm}=180000\text{\,cm}$
Größe der Karte bei gegebenem Maßstab prüfen
Ein Maßstab von $1:10000$ bedeutet, $1\text{\,cm}$ auf der Karte entsprechen $10000\text{\,cm}$ in Wirklichkeit.
Bei einem Maßstab von $1:10000$ entsprechen $180000\text{\,cm}$ in Wirklichkeit $18\text{\cm}$ auf der Karte.
Da die Informationsbroschüre nur $10{,}5\text{\,cm}$ breit und $14{,}5\text{\,cm}$ lang ist, kann die Altstadt beim Maßstab von $1:10000$ weder in der Länge noch in der Breite abgebildet werden.
Rechne die Längen in eine einheitliche Einheit um
Berechne, wie viel Platz die Karte beim vorgegebenen Maßstab benötigt
4
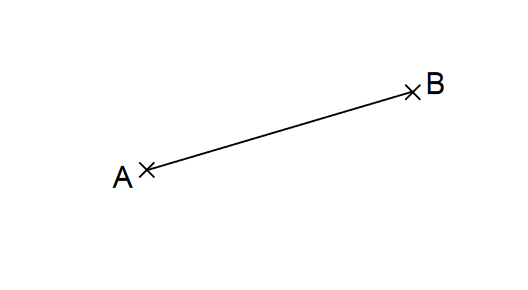
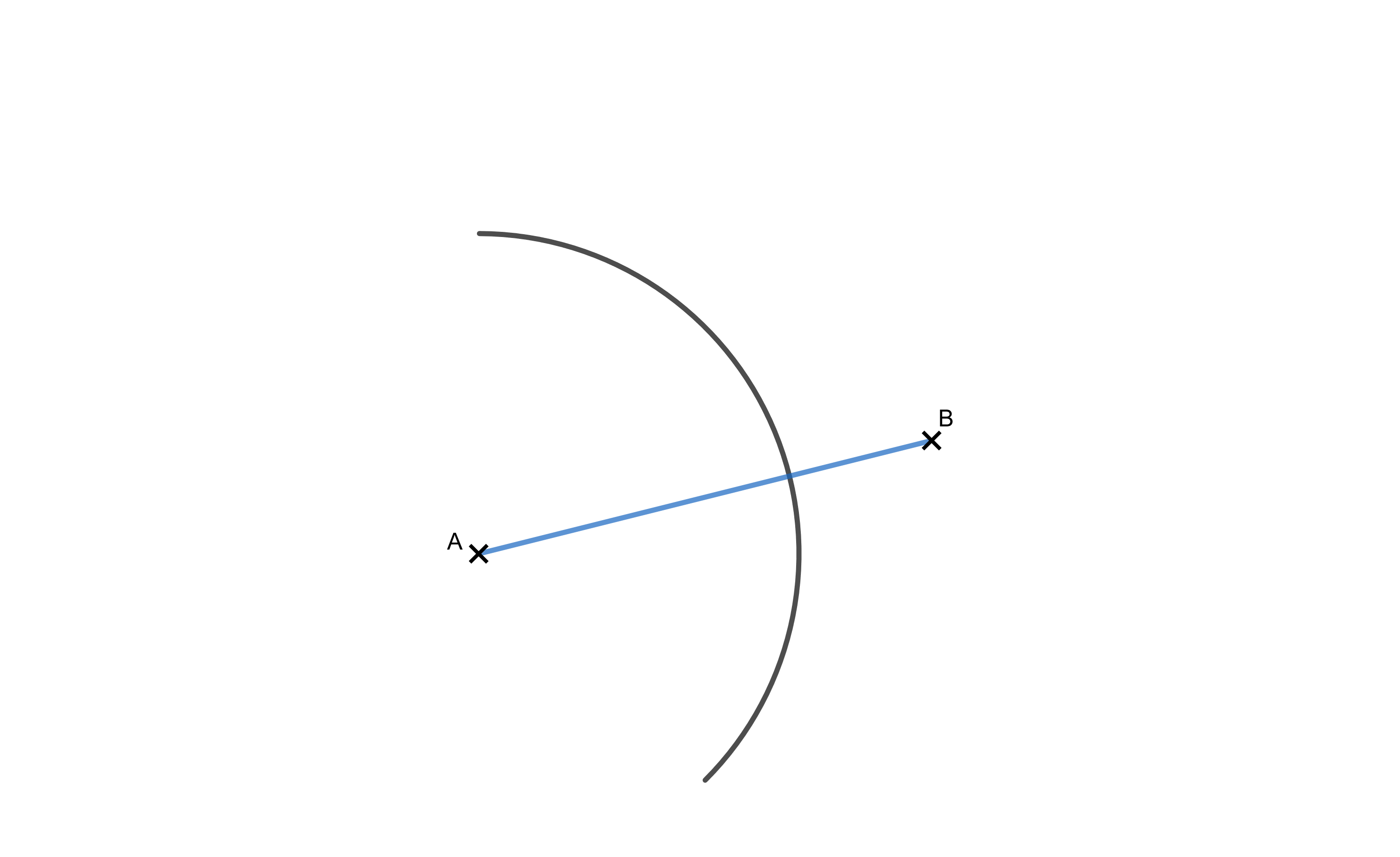
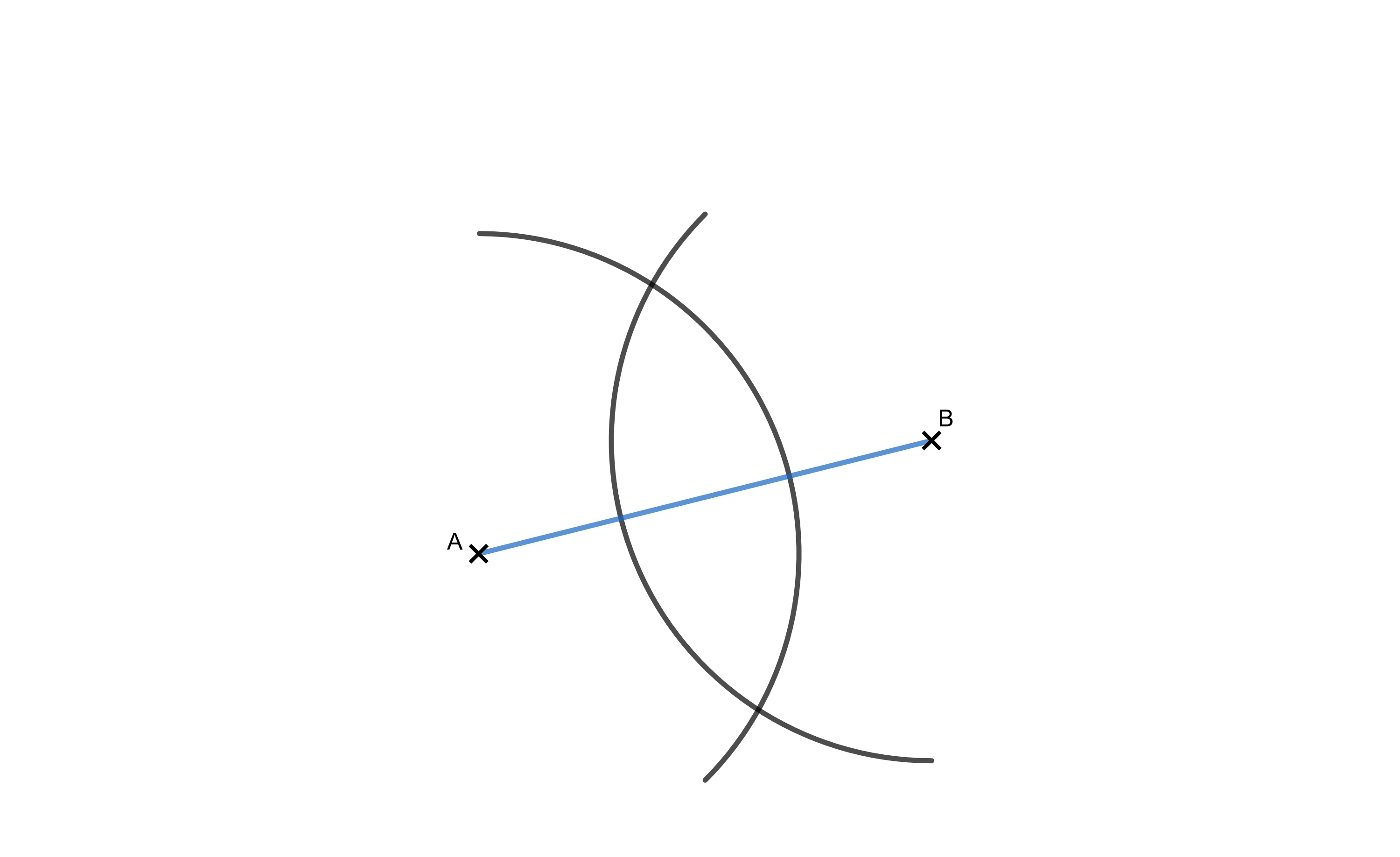
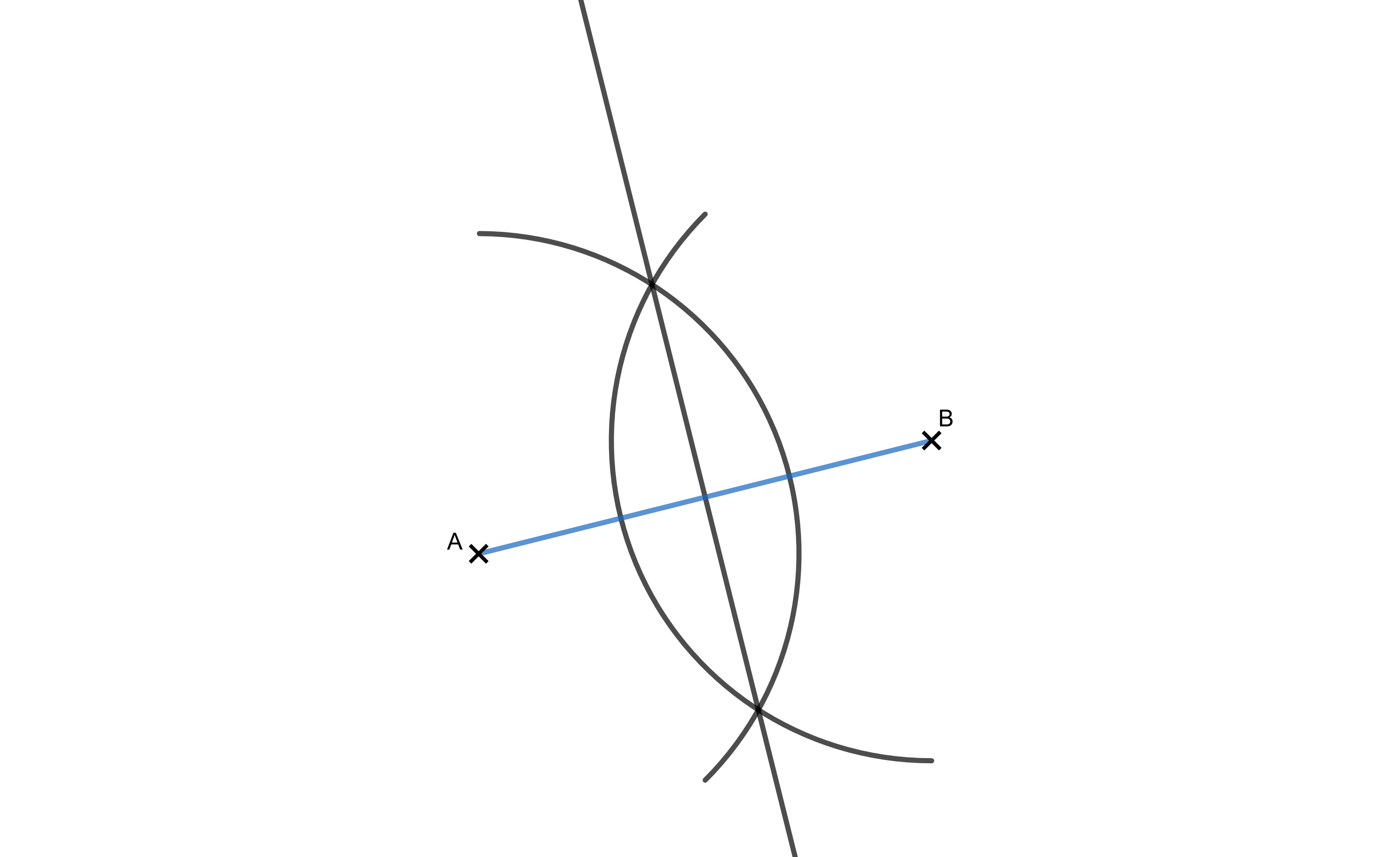
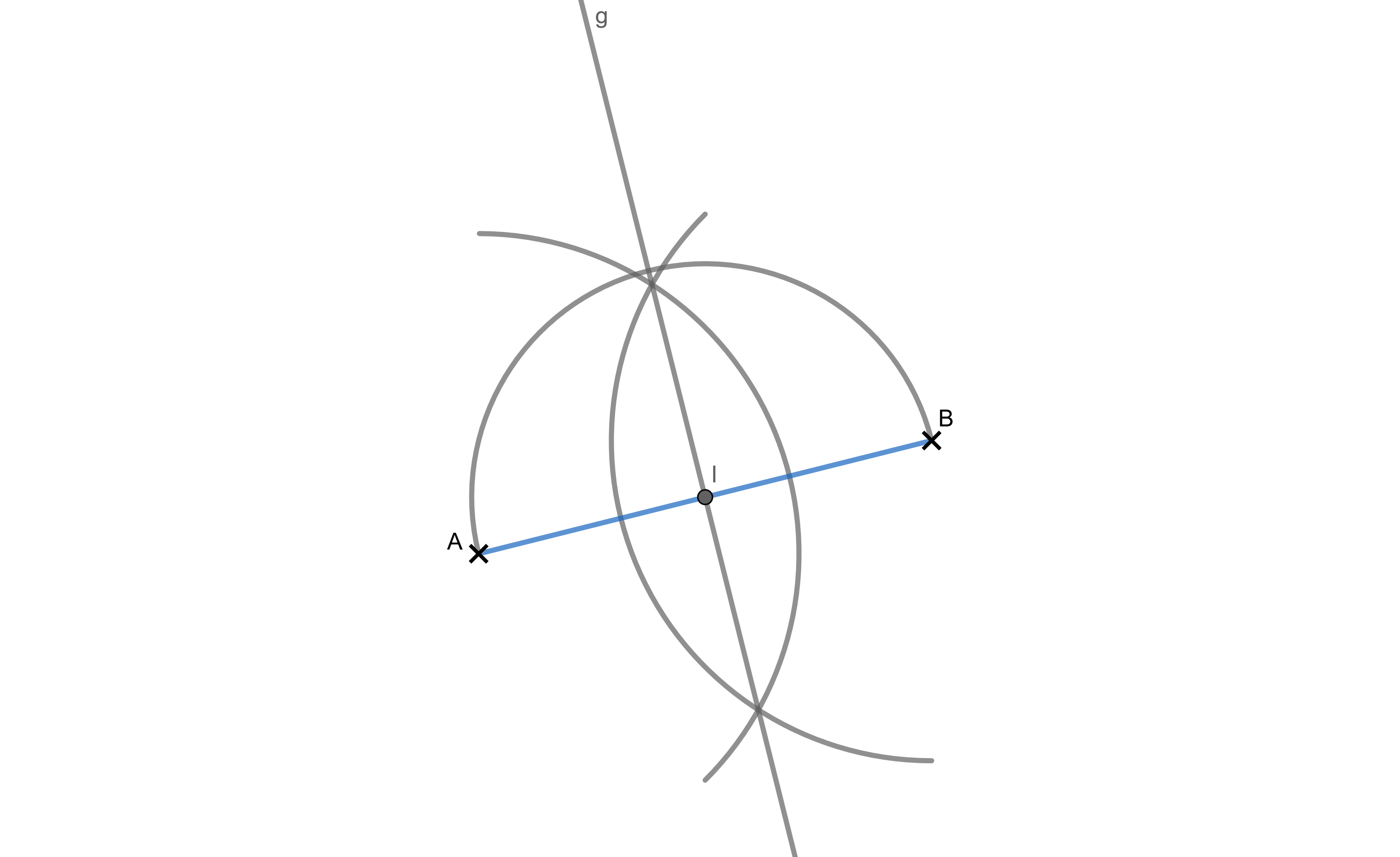
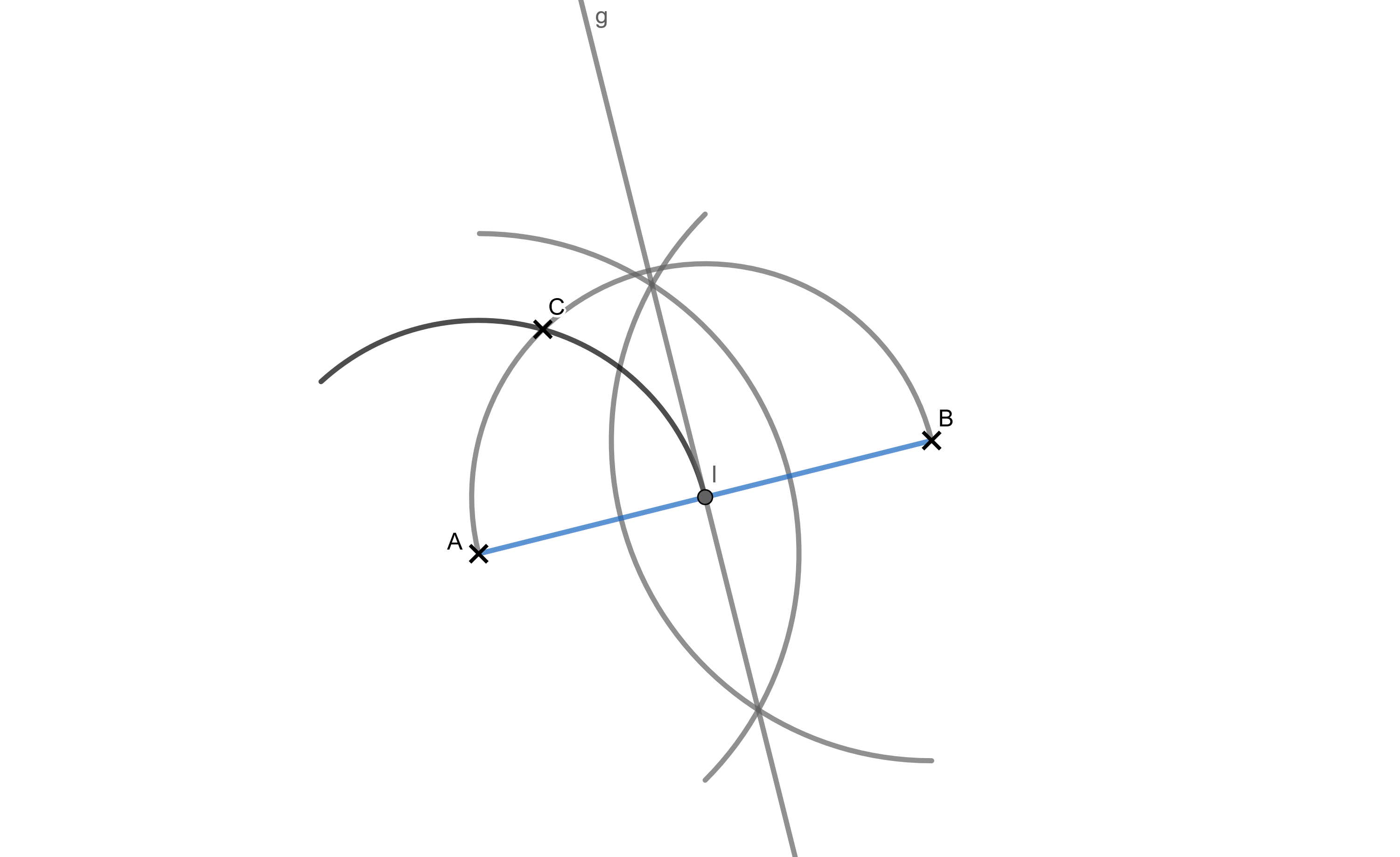
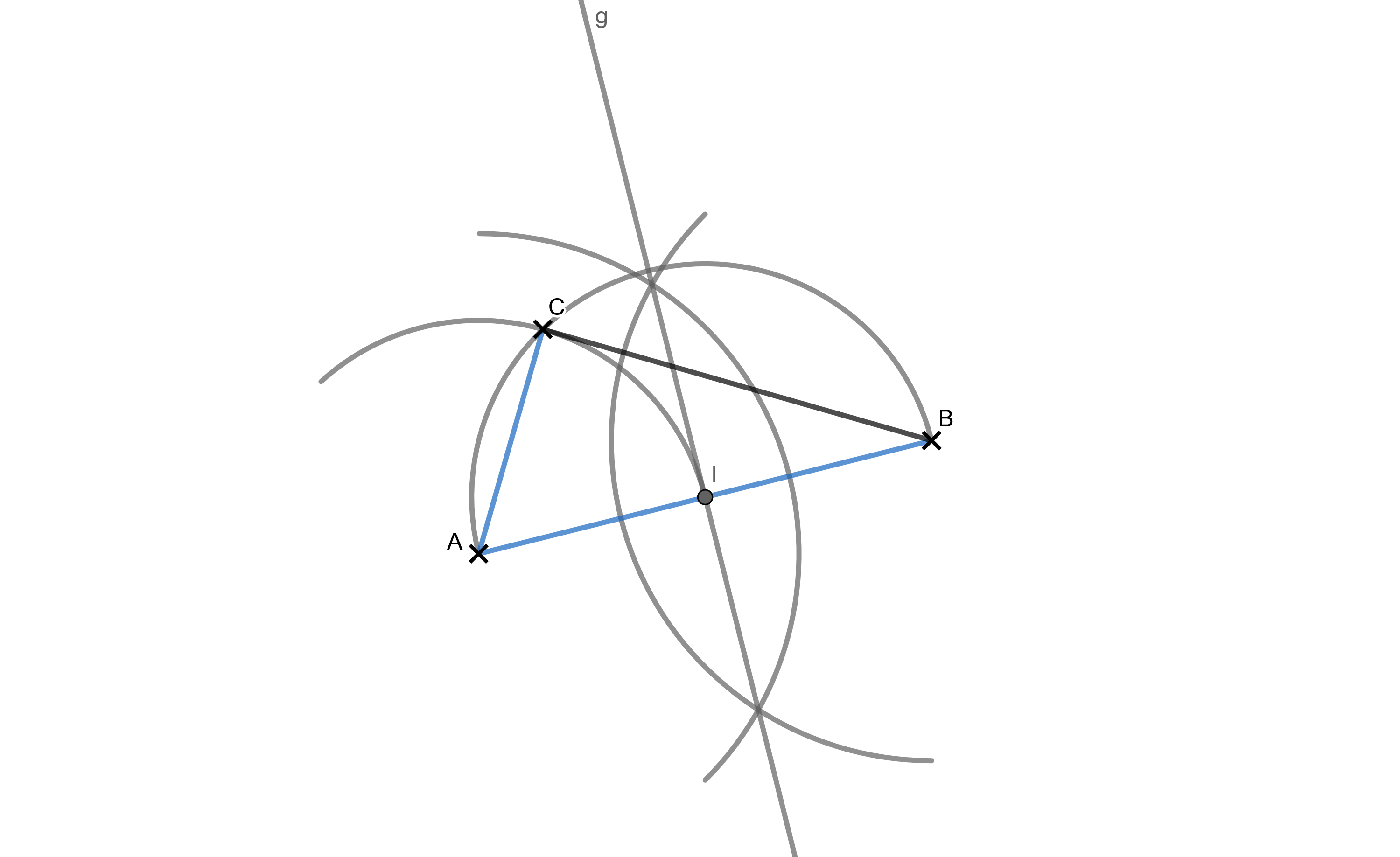
Die Abbildung zeigt die Hypotenuse eines rechtwinkligen Dreiecks $ABC$ . Konstruiere den Punkt $C$ so, dass die Kathete $[AC]$ halb so lang ist wie die Hypotenuse. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Mittelsenkrechte
1.Zeichne einen Kreis um A, dessen Radius größer ist als der halbe Abstand zwischen A und B.
2. Nun Zeichne ebenfalls einen Kreis mit dem gleichen Radius um B.
3. Als nächstes wird die Mittelsenkrechte g eingezeichnet. Sie entsteht, wenn man eine Gerade durch die beiden Schnittpunkte der Kreise zeichnet.
4. Der Schnittpunkt der Strecke AB und der Mittelsenkrechten ergibt einen Punkt (I). Nun benutzen wir den Satz des Thales, damit unser Dreieck rechtwinklig wird. Das heißt es wird ein Kreis um I mit dem Radius AI gezogen.
5. Da die Strecke AC halb so lang sein soll wie die Strecke AB, wird ein Kreis um A gezogen, welcher den Radius AI hat (mit Hilfe der Mittelsenkrechten hatten wir den Mittelpunkt der Strecke AB ermittelt, somit ist I der Mittelpunkt der Strecke). Der Schnittpunkt ergibt den Punkt C.
6. Zu guter Letzt werden die Punkte A, B und C verbunden. Nun haben wir ein rechtwinkliges Dreieck, wo die Seite AC halb so lang ist wie die vorgegebene Strecke AB.
5
Bei einer Spielshow treten zwei Kontrahenten in einem Wettkampf, der aus zehn Spielen besteht, gegeneinander an. Jedes Spiel hat einen Sieger, der beim ersten Spiel einen Punkt, beim zweiten Spiel zwei Punkte usw. erhält und einen Verlierer, der jeweils keinen Punkt erhält. Ist es möglich, dass am Ende dieses Wettkampfs beide Kontrahenten gleich viele Punkte erhalten haben? Begründe deine Antwort. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition
In den 10 Spielen gibt es
im 1. Spiel einen Punkt
im 2. Spiel zwei Punkte
im 3. Spiel drei Punkte
usw.
zu gewinnen.
Zusammen sind das
$1+2+3+4+5+6+7+8+9+10=55$ Punkte.
Weil $55$ eine ungerade Zahl ist, kann man sie nicht in zwei gleich große natürliche Zahlen aufteilen.
Daher ist es nicht möglich, dass beide Spieler am Ende die gleiche Punktzahl haben.
6
Gegeben ist der Term $3{,}5 \;\mathrm{kg}:100\;\mathrm{g}$ .
1. Berechne den Wert des Terms. (1 BE)
  $3{,}5 \;\mathrm{kg}:100\;\mathrm{g}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Mengeneinheiten
  Berechne den Wert des Terms.
  $3{,}5\ kg:100\ g=3500\ g:100\ g=35$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Formuliere eine Sachaufgabe, die mithilfe des Terms gelöst werden kann. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Mengeneinheiten
  Formuliere eine Sachaufgabe, die mithilfe des Terms gelöst werden kann.
  $3{,}5\ kg$ Schokolade werden zu Tafeln mit einem Gewicht von je $100\ g$ aufgeteilt. Wie viele Tafeln Schokolade ergibt das?
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Vereinfache jeweils so weit wie möglich. (je 1 BE)

$-20+(-2)^3$

Berechne zunächst die Klammer
↓
$\displaystyle -20+(-2)^3$ $=$ $\displaystyle -20-8$
↓
Fasse zusammen
$=$ $\displaystyle -28$
Die Vereinfachung lautet $-28$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$4 \;\mathrm{c}^2-(4c-7)\cdot c$

8
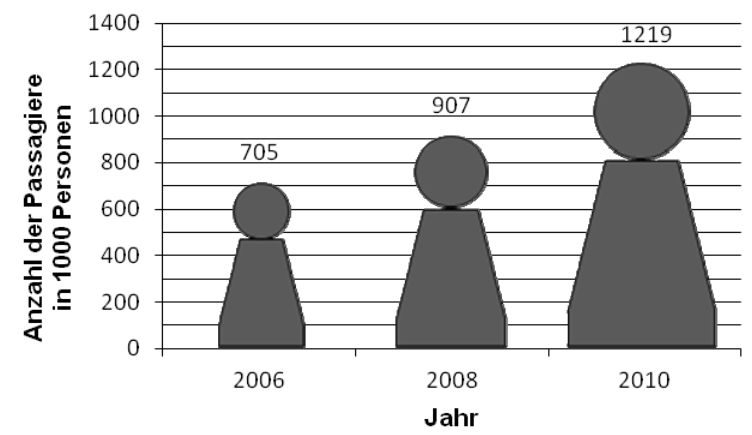
Das Diagramm zeigt für Kreuzfahrten deutscher Reiseveranstalter die Entwicklung der Anzahl der Passagiere.
1. Wähle aus, um wie viel Prozent die Anzahl der Passagiere zwischen 2006 und 2010 ungefähr gestiegen ist. (1 BE)
  40 %
  50 %
  60 %
  70 %
  80 %
  
  2006 waren auf dem Schiff 705 Passagiere und 2010 waren es 1219 Passagiere. Um zu berechnen, wie sich das Passagieraufkommen vergrößert hat, brauchst du Methoden der Prozentrechnung.
  $\dfrac {1219} {705} = 1{,}729$
  Zwischen 2006 und 2010 ist die Anzahl der Passagiere also um ca. $70\ \%$ gestiegen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Figuren im Diagramm könnten den Eindruck erwecken, dass die Anzahl Passagiere zwischen 2006 und 2010 deutlich stärker stieg als dies tatsächlich der Fall war. Beschreibe die Ursache für diesen Eindruck. (1 BE)
  
  Der Eindruck wird übermittelt, da die Figur nicht nur in die Höhe sondern auch in die Breite gewachsen ist. In Folge dessen wird auch die Fläche der Person größer.
  Jedoch soll nur die Höhe und nicht der Flächeninhalt der Figuren das Passagierwachstum verdeutlichen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Die Passagiere eines Kreuzfahrtschiffs beobachten gerne die Ablegemanöver ihres Schiffs. Besonders begehrt sind dabei die Plätze direkt am Geländer, das das obere Deck des Schiffs vollständig umgibt. Dieses Deck hat näherungsweise die Form eines Rechtecks der Länge $175\ m$ und der Breite $30\ m$ . Schätze ab, wie viele Passagiere nebeneinander auf den besonders begehrten Plätzen stehen können. (2 BE)
  Hinweis: Bei einer Abschätzung muss grundsätzlich der Lösungsweg nachvollziehbar sein.
  
  Als Erstes muss der Umfang des Decks berechnet werden. Dazu müssen die vier Seiten des Rechtecks addiert werden.
  Nun muss überlegt werden, welche Durchschnittsbreite ein Mensch hat. Du kannst zum Beispiel eine Breite von $55\text{cm}$ annehmen. Daraufhin wird die Länge des Geländers durch die umgerechnete Breite von $55\text{cm}$ , also $0{,}55\text{m}$ , geteilt.
  Vergiss nicht deine Lösung in einem Satz zusammenzufassen!
  Es haben ca. $745$ Personen an den begehrten Plätzen direkt am Geländer Platz.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
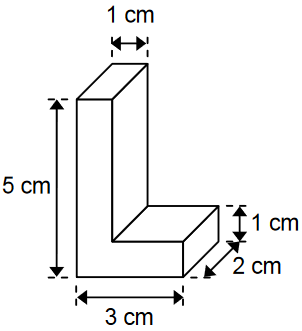
Lukas hat aus Tonpapier einen Körper hergestellt, der die Form des Buchstabens „L" hat (vgl. nebenstehende Abbildung).
1. Berechne das Volumen des Körpers. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen
  Das Volumen eines Quaders berechnet sich wie folgt:
  $V=l\cdot b\cdot h$
  Der L-förmige Körper, den Lukas gezeichnet hat, setzt sich aus 2 Teilkörpern zusammen, einem senkrechten Körper $V_{1}$ und einem waagrechten Körper $V_{2}$ . Die beiden Volumina errechnen sich wie folgt.
  $V_1=1\ cm\cdot2\ cm\cdot4\ cm=8\ cm^3$
  $V_2=3\ cm\cdot2\ cm\cdot1\ cm=6\ cm^3$
  $V=V_1+V_2=14\ cm^3$
  Das Volumen des gesamten Körpers beträgt $14\ cm^3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
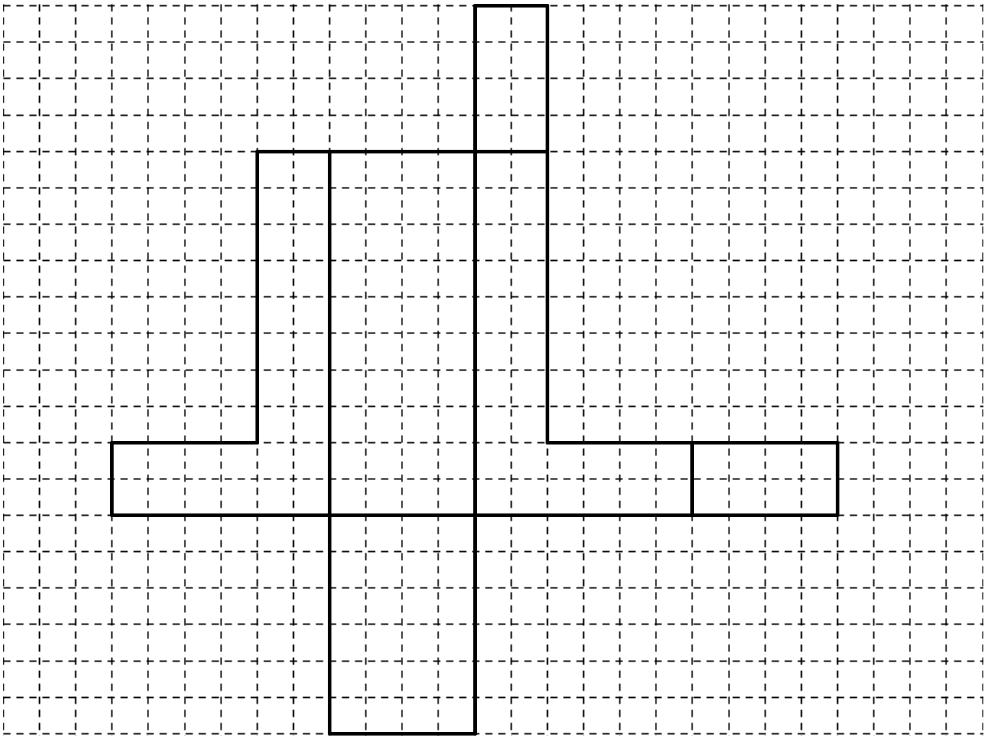
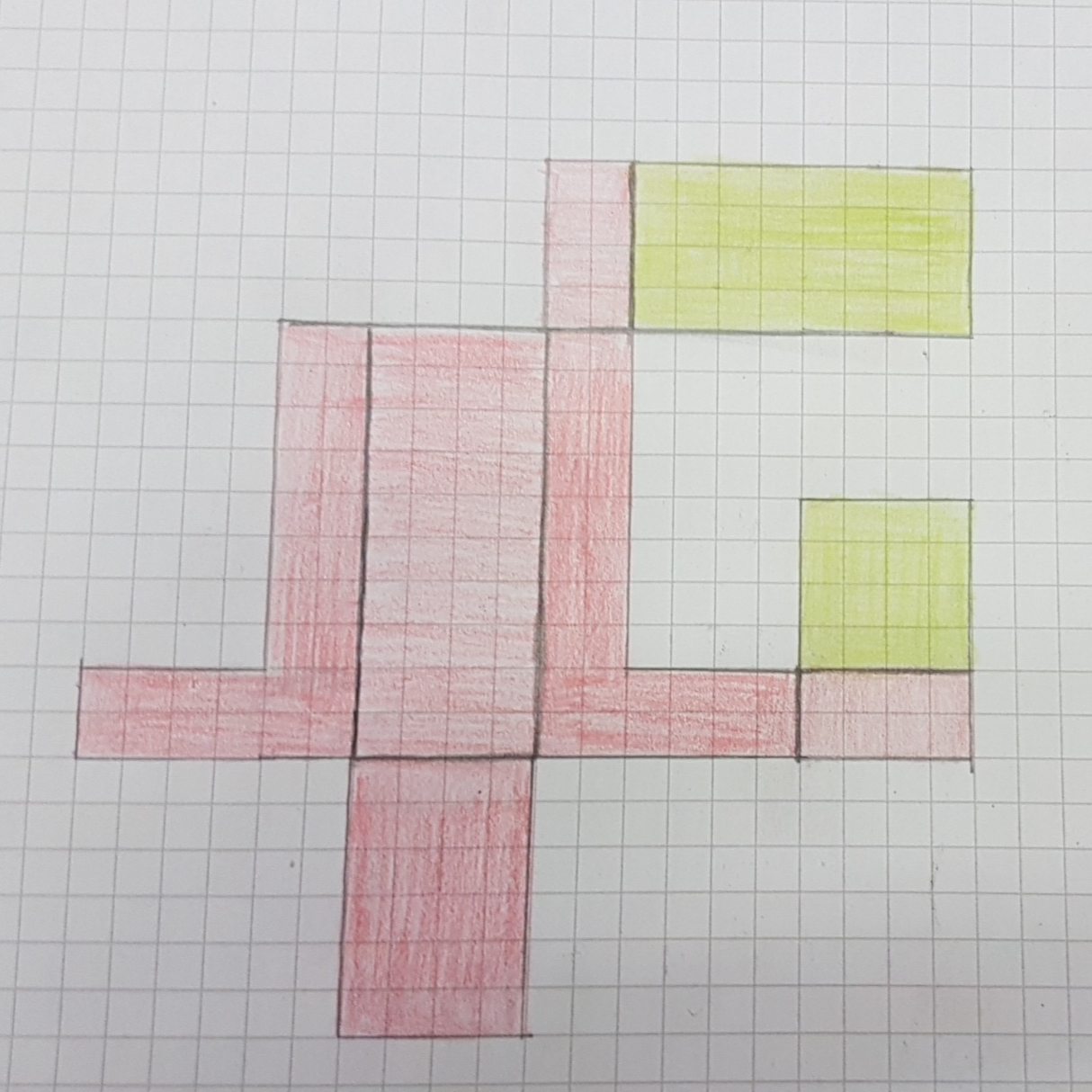
2. Trage in die folgende Abbildung zusätzliche Linien so ein, dass ein Netz des Körpers entsteht (Klebefalze müssen nicht berücksichtigt werden). (2 BE)
  
  Eine Beispiel-Lösung:
  Man erhält die richtige Form, indem man die fehlenden Seiten vom L an den richtigen Positionen ergänzt.
  Es sind verschiedene Lösungen möglich. Um nachzuprüfen, dass eine Form wirklich richtig ist, sollte man das Netz ausschneiden und versuchen das L nachzubasteln.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Berechne zunächst die Klammer
	↓
$\displaystyle -20+(-2)^3$	$=$	$\displaystyle -20-8$
	↓	Fasse zusammen
	$=$	$\displaystyle -28$

Multipliziere zunächst die Klammer.
	↓
$\displaystyle 4c^2-(4c-7)\cdot c$	$=$	$\displaystyle 4c^2-(4c^2-7c)$
	↓	Löse die Klammer auf.
	$=$	$\displaystyle 4c^2-4c^2+7c$
	↓	Fasse zusammen
	$=$	$\displaystyle 7c$

Gruppe A

Umrechnen der Längen

Größe der Karte bei gegebenem Maßstab prüfen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?