Konstruktion des Thaleskreises

Zeichne eine Strecke $[AB]$ mit der Länge $6\mathrm{cm}$.

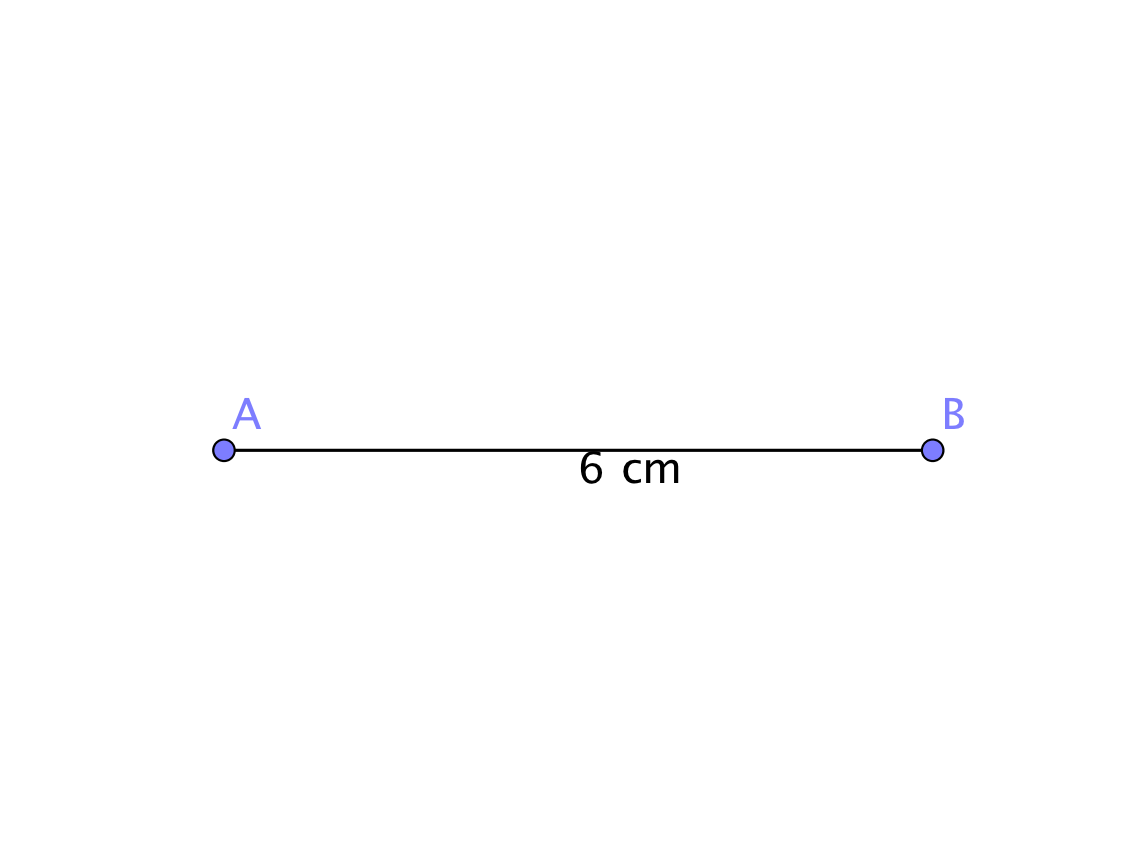
Konstruiere die Mittelsenkrechte $g$ zu den Punkten $A$ und $B$. Der Schnittpunkt der Mittelsenkrechten mit der Strecke $[AB]$ ist der Mittelpunkt $M$ von $A$ und $B$.

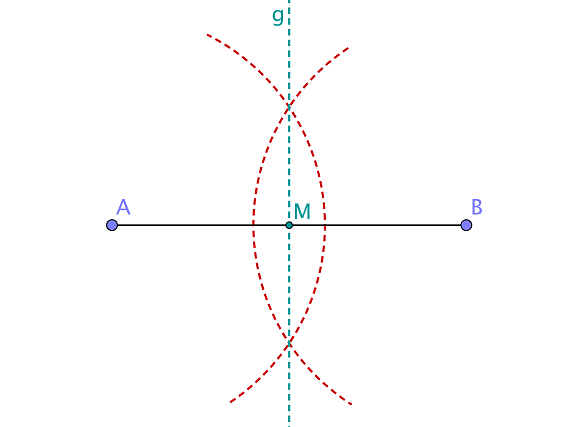
Zeichne den Thaleskreis, indem du einen Kreis mit Mittelpunkt $M$ durch $A$ und $B$ ziehst.

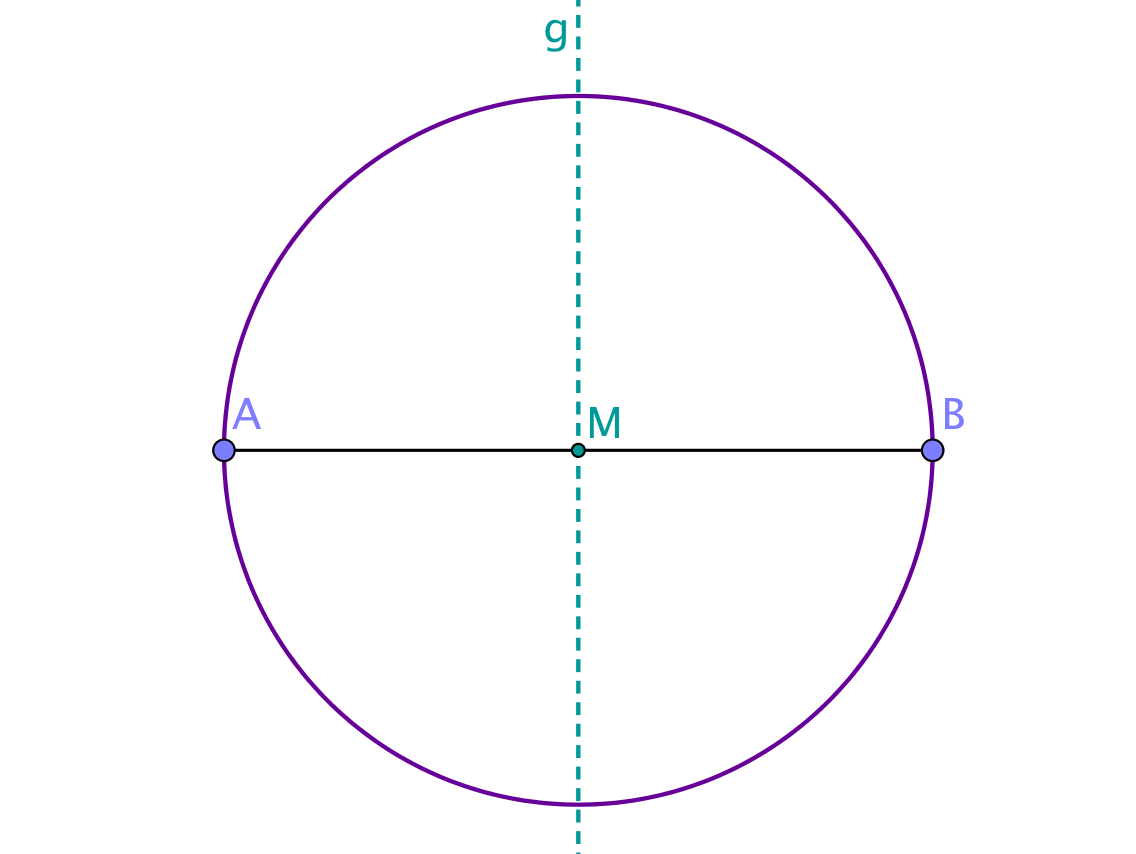
Konstruktion einer Parallelen

Nun musst du eine Parallele mit $\mathrm{1,5}\mathrm{cm}$ Abstand zur Strecke $[AB]$ konstruieren. Zeichne dafür zuerst einen Punkt $P$ auf der Mittelsenkrechten $g$, sodass der Abstand vom Mittelpunkt $M$ zu $P$ $\mathrm{1,5}\mathrm{cm}$ beträgt.

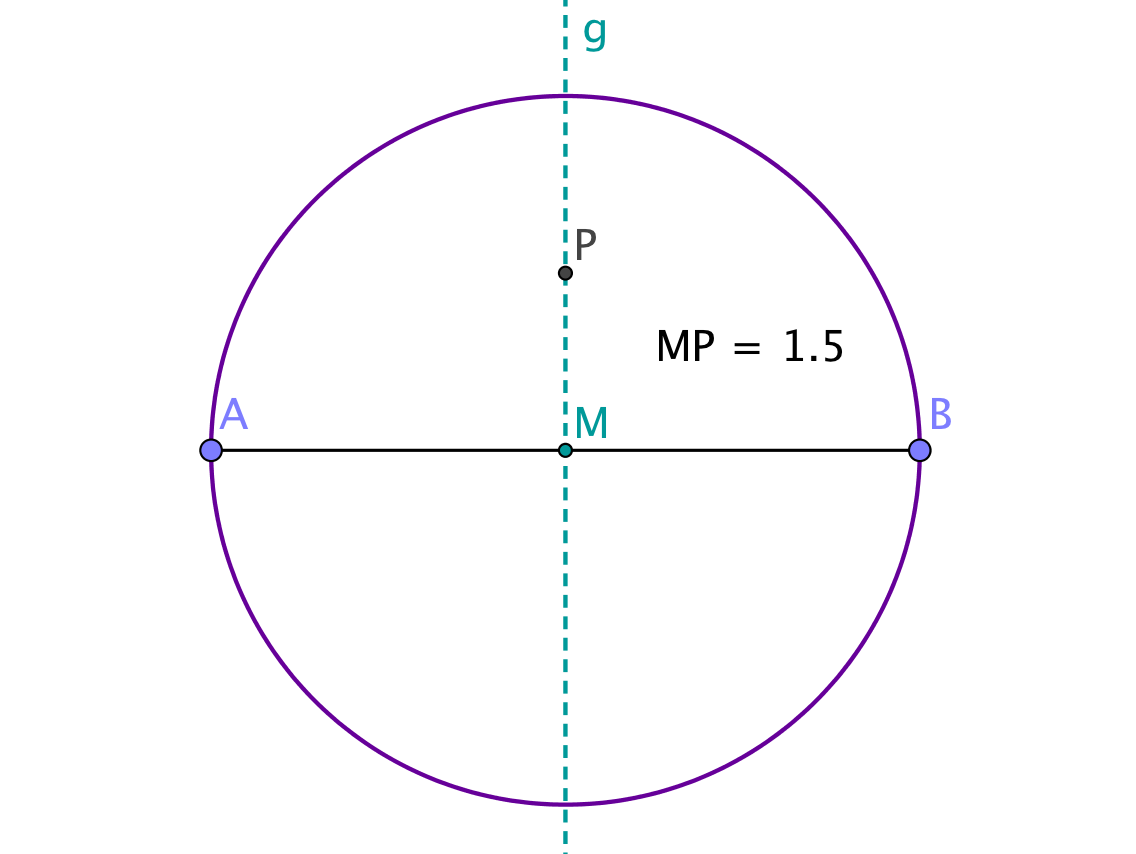
Ziehe nun einen Kreis mit Kreismittelpunkt $P$ und beliebigem Radius. Finde die Schnittpunkte $R$ und $S$ des Kreises mit der Mittelsenkrechten $g$.

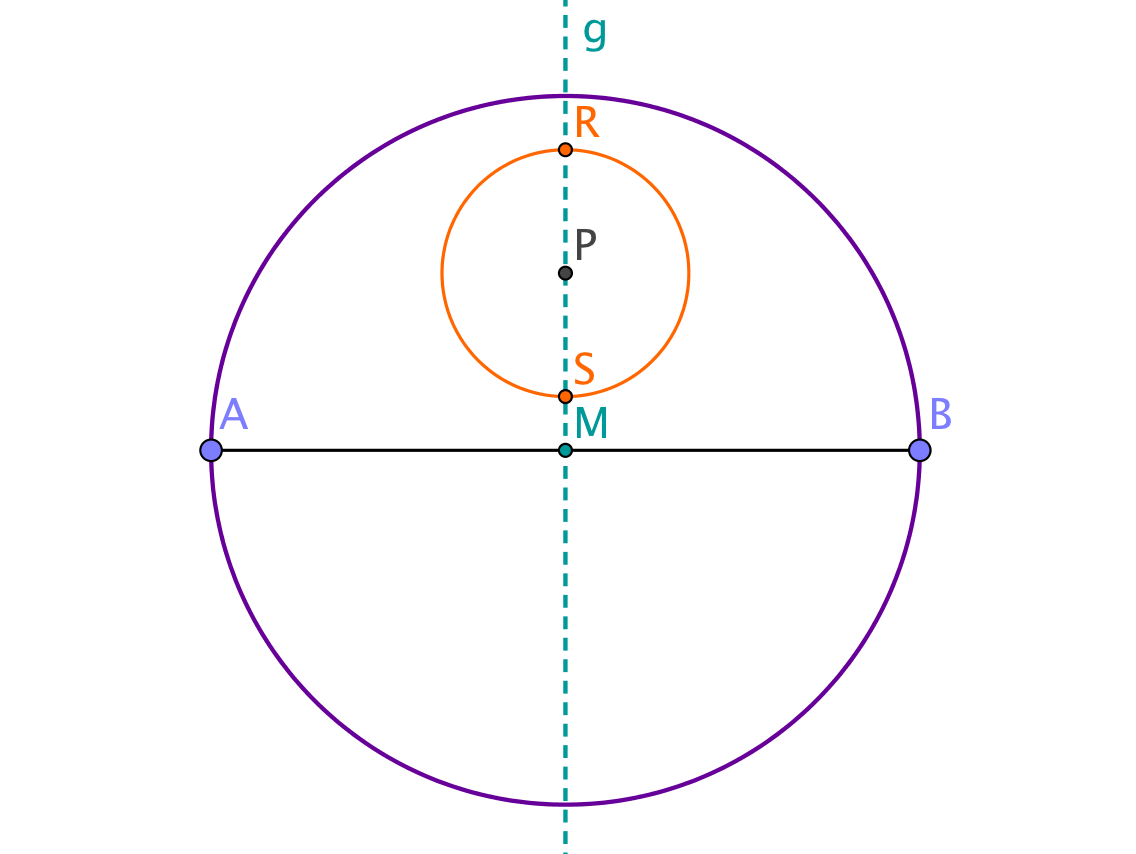
Wie oben kannst du nun die Mittelsenkrechte zu $R$ und $S$ konstruieren. Dadurch erhältst du eine zu $[AB]$ parallele Gerade mit Abstand $\mathrm{1,5}\mathrm{cm}$.

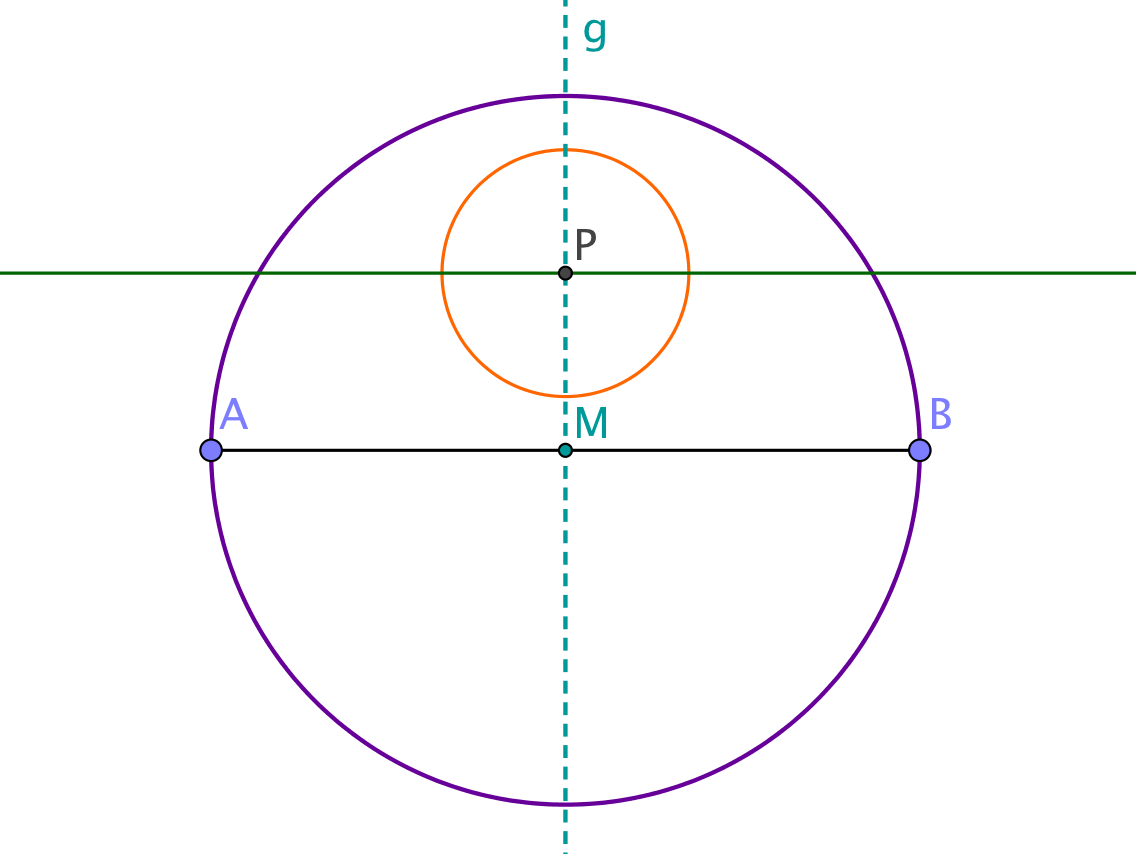
Konstruktion des rechtwinkligen Dreiecks

Der Schnittpunkt der parallelen Geraden mit dem Thaleskreis liefert die gesuchte Ecke $C$ des Dreiecks $ABC$. Durch Verbinden des Punktes $C$ mit den Punkten $A$ und $B$ erhältst du das gesuchte rechtwinklige Dreieck mit Seitenlänge $\overline{AB}=6\mathrm{cm}$ und Höhe $h=\mathrm{1,5}\mathrm{cm}$.

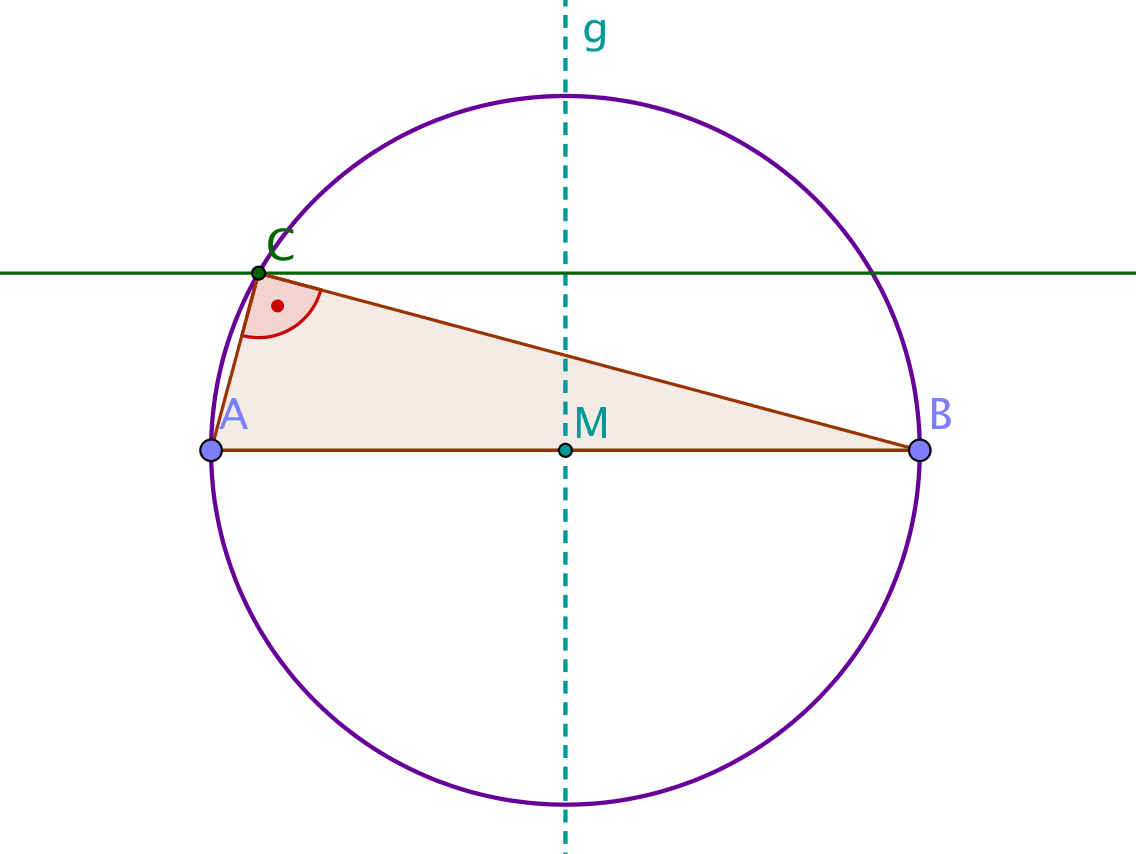
Wie du oben siehst, gibt es einen zweiten Schnittpunkt der parallelen Geraden mit dem Thaleskreis. Dadurch erhältst du eine zweite Lösung (orange).

Lösungen $3$ (lila) und $4$ (blau) erhältst du durch Spiegelung der Eckpunkte an der Strecke $[AB]$.

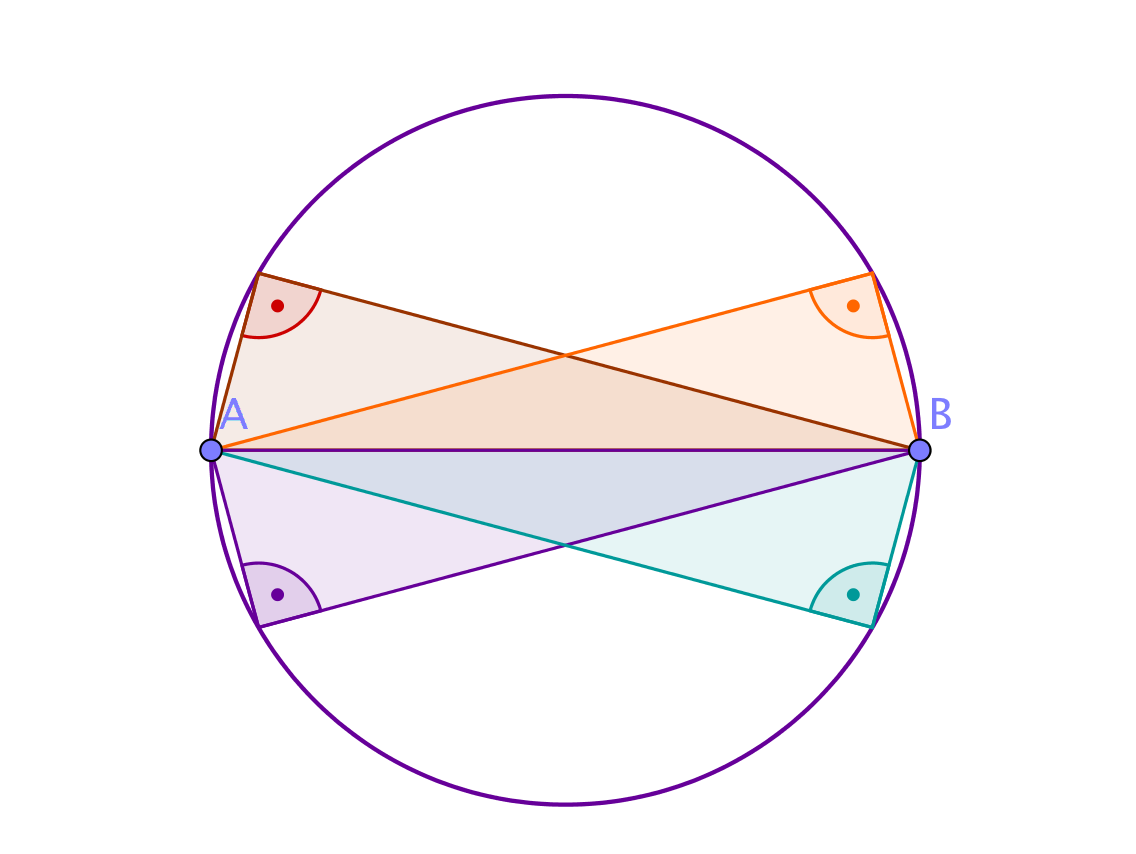
Alle 4 rechtwinkligen Dreiecke erfüllen die Anforderungen der Aufgabenstellung, da sie die Höhe $h=\mathrm{1,5}\mathrm{cm}$ und Seitenlänge $\overline{AB}=6\mathrm{cm}$ haben.