Schätze den Wert von .
Berechne dazu die ersten vier Schritte des Heron-Verfahrens und schätze anschließend den Wert von .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Heron-Verfahren
Heron-Verfahren
Das Heron-Verfahren ist eine Methode, um den Wert von Wurzeln (schrittweise) abzuschätzen.
Du suchst ein Quadrat, dessen Flächeninhalt genau dem Radikanden entspricht. Dazu bildest du zuerst ein Rechteck, dessen Seiten du Schritt für Schritt veränderst.
1. Schritt
Das erste Rechteck findest du, indem du einen Teiler des Radikanden suchst und dann die zweite Seite durch Auflösen der Formel für den Flächeninhalt für Rechtecke.
entspricht dem Radikanden. In unserem Fall ist und nur durch und sich selbst teilbar. Daraus ergeben sich unsere Anfangswerte und .
Im Bild unten siehst du das anfängliche Rechteck.
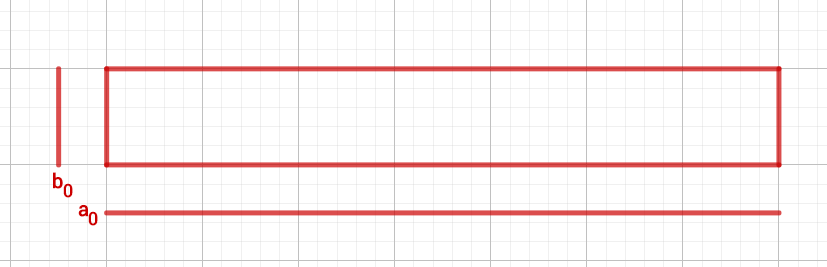
Die nächsten Schritte laufen immer in der folgenden Reihenfolge ab:
Zuerst bildest du den Mittelwert der alten Werte und berechnest daraus dein neues .
findest du, indem du rechnest und dort das neue einsetzt und den Radikanden für .
Eine ausführliche Erklärung dieser Schritte findest du hier.
2. Schritt
Bilde den Mittelwert von und .
Berechne anschließend .
Deine neuen Werte:
Im Bild unten siehst du das ursprüngliche Rechteck und das neue, das sich mehr einem Quadrat angenähert hat.
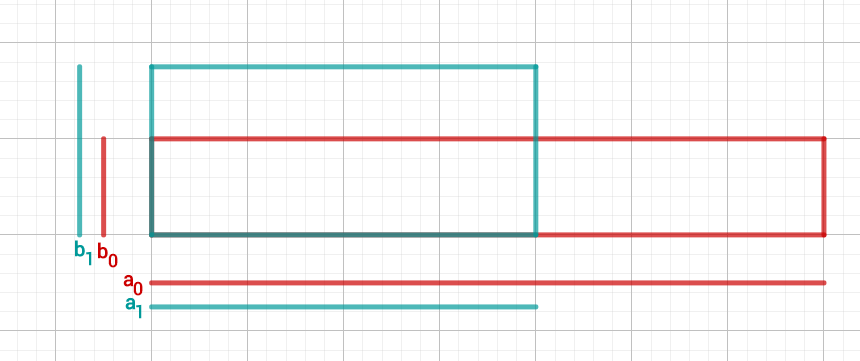
3. Schritt
Bilde den Mittelwert von und .
Berechne anschließend .
Deine neuen Werte sind:
Im Bild unten siehst du die Veränderung der Rechtecke.
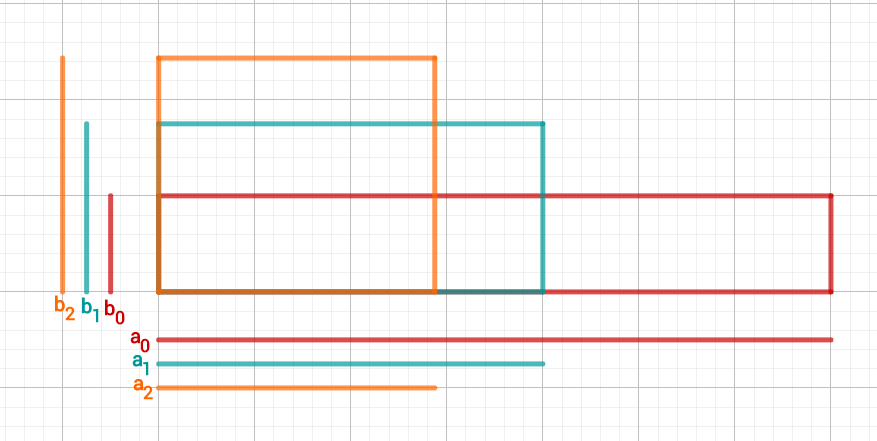
4. Schritt
Bilde den Mittelwert von und .
Berechne nun .
Deine endgültigen Werte sind und .
Wie dir auffällt, haben sich die beiden Werte sehr stark angenähert.
Im Bild unten siehst du die Veränderung der Rechtecke. Das letzte (lila) ist schon nah an einem Quadrat.
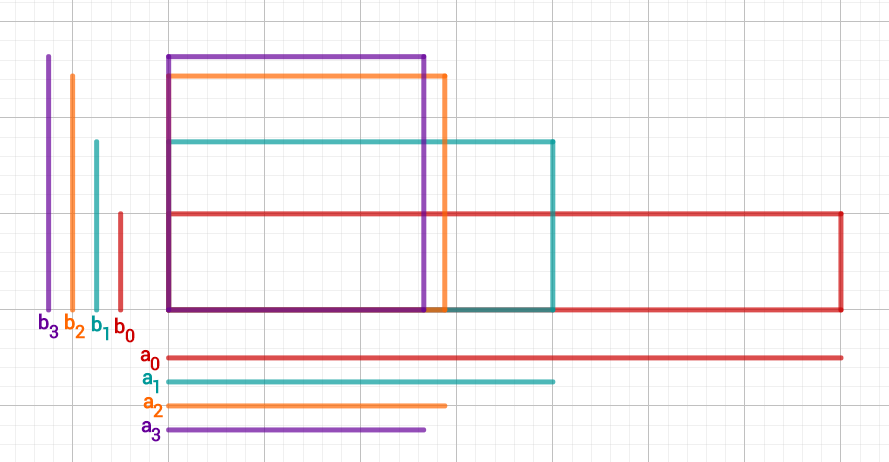
Abschätzung
Für die Abschätzung bildest du nochmal den Mittelwert zwischen den beiden letzten Seiten.
Zum Vergleich: Wenn du den Wert im Taschenrechner berechnest, erhältst du den gerundeten Wert: .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
