Hauptnenner mit Variablen

Dieser Artikel befasst sich mit dem Herausfinden von Hauptnennern bei Bruchgleichungen.

Der Hauptnenner ist das kleinste gemeinsame Vielfache der Nenner. Auch beim Hauptnenner mit Variablen suchst du das kleinste gemeinsame Vielfache der Nenner. "Auf den Hauptnenner bringen" bedeutet, die Brüche alle so zu erweitern oder zu kürzen, dass sie diesen Nenner besitzen. Dies ist z.B. notwendig, um ihre Größe zu vergleichen und sie zu addieren oder zu subtrahieren.

\displaystyle \frac{2}{3}+\frac{1}{4}=\frac{2\cdot4}{3\cdot4}+\frac{1\cdot3}{4\cdot3}=\frac{8}{12}+\frac{3}{12}=\frac{11}{12}

Rechnerisches Vorgehen

Anders als beim Hauptnenner Finden ohne Variablen wendet man hier nicht die Primfaktorzerlegung an, sondern geht auf die Suche nach "Bausteinen".

Bausteine sind die Faktoren der Nenner. Den Hauptnenner bekommst du, indem du die Bausteine multipliziert. Dabei verwendest du Bausteine, die in mehreren Nennern vorkommen, nur einmal.

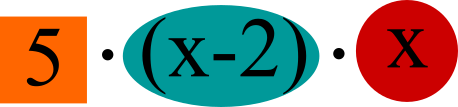
Die beiden Brüche erweitert man nun so, dass ihre Nenner dieselben Bausteine enthalten. Daraufhin sind die Brüche auf einem Hauptnenner.

Beispiel 1

$\displaystyle\frac{1}{x}+\frac{2}{x+2}$

Die Bausteine hier sind:

[ $x$ ]
[ $x+2$ ]

Hauptnenner:

$[x]\cdot[x+2]$

Den Hauptnenner erhältst du als Produkt der Bausteine. Überprüfe hier zuerst, ob Bausteine doppelt vorkommen. Wenn ein Baustein doppelt vorkommt, benötigst du diesen nur einmal.

Hilfsmittel

Da die Bausteine der Nenner oft nicht direkt sichtbar sind, nutzt du zuerst folgende Hilfsmittel: Faktorisieren und Kürzen.

Beispiel 2

Nun betrachten wir eine Bruchgleichung :
	↓
$\displaystyle \frac{1}{x^2+3x}$	$=$	$\displaystyle \frac{4}{5x_{ }}$
	↓	Faktorisiere, wenn möglich
$\displaystyle \frac{1}{x\left(x+3\right)}$	$=$	$\displaystyle \frac{4}{5x}$
	↓	Durch Faktorisieren erhältst du diese Gleichung. Wenn möglich, kürze die Brüche. Dies ist in der gegebenen Gleichung nicht möglich.
$\displaystyle \frac{1}{x\left(x+3\right)}$	$=$	$\displaystyle \frac{4}{5x}$

Hier kannst du die Bausteine ablesen:

$[x]$
$[x+3]$
$[5]$
$[x]$

$[x]\;\;\;$	$[x+3]$
$[x]$		$[5]$
$\;\Downarrow$	$\;\;\;\Downarrow$	$\Downarrow$
$[x]$	$[x+3]$	$[5]$

Links siehst du in den Zeilen die Bausteine der einzelnen Nenner. Sie sind so angeordnet, dass gleiche Bausteine untereinander stehen.

Den Hauptnenner erhältst du, indem du aus jeder Spalte ein Element auswählst und das Produkt bildest.

Somit ist der Hauptnenner:

$[x]\cdot[x+3]\cdot[5]$

Beispiel 3

Im folgenden Beispiel ist, wie in Beispiel 1 wieder einen Bruchterm. Du solltest hierfür bereits die binomischen Formeln kennen.

$\displaystyle \frac{1}{x}+\frac{5}{x^2}-\frac{x+1}{x^2+2x+1}$	$=$
	↓	Faktorisiere, wenn möglich.
	$=$	$\displaystyle \frac{1}{x}+\frac{5}{x^2}-\frac{x+1}{\left(x+1\right)^2}$
	↓	Durch Anwendung der 1. binomischen Formel erhältst du diese Gleichung. Kürze nun, wenn möglich. Nach dem Kürzen erhältst du den folgenden Term.
	$=$	$\displaystyle \frac{1}{x}+\frac{5}{x^2}-\frac{1}{\left(x+1\right)}$
	↓	Nach dem Kürzen erhältst du diesem Term.

$[x]$
$[x]$	$[x]$
		$[x+1]$
$\Downarrow$	$\Downarrow$	$\;\;\;\Downarrow$
$[x]$	$[x]$	$[x+1]$

Nun kannst du folgende Bausteine ablesen:

$[x]$
$\lbrack x\rbrack \cdot \lbrack x\rbrack$
$[x+1]$

Links siehst du in den Zeilen die Bausteine der einzelnen Nenner. Sie sind so angeordnet, dass gleiche Bausteine untereinander stehen.

Den Hauptnenner erhältst du, indem du aus jeder Spalte ein Element auswählst.

Somit ist der Hauptnenner:

$\lbrack x\rbrack \cdot \lbrack x\rbrack \cdot[x+1]$

Übungsaufgaben

Inhalt wird geladen…

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Umgang mit Bruchtermen

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Brüche kürzen und erweitern

Kurse

Bruchterme durch Kürzen vereinfachen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?