Aufgaben zum Umgang mit Bruchtermen

Vereinfache so weit wie möglich.

$\dfrac{a+b}b-\dfrac{a-b}a$

$\dfrac c{c^2-8c+16}-\dfrac2{c^2-6c+8}$

$\dfrac{b-c}{a^2+ac}-\dfrac{a-b}{ac+c^2}+\dfrac{a^2+c^2}{a^2c+ac^2}$

$\dfrac{10u^2-11u-6}{25u^2-4}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellenform einer quadratischen Gleichung
Nenner vereinfachen
$\frac{10u^2-11u-6}{25u^2-4}$
$\frac{10u^2-11u-6}{(5u-2)\cdot (5u+2)}$
Die dritte binomische Formel auf den Nenner anwenden.
Zähler seperat faktorisieren
${10u^2-11u-6}=0$
Zähler separat mit Hilfe der Mitternachtsformel faktorisieren.
$u_{1{,}2}=\frac{-(-11) \pm \sqrt{(-11)^2-4 \cdot 10 \cdot (-6)}}{2 \cdot 10}$
$u_{1{,}2}=\frac{11 \pm \sqrt{121+240}}{20}$
$u_{1{,}2}=\frac{11 \pm \sqrt{361}}{20}$
$u_{1{,}2}=\frac{11 \pm 19}{20}$
Eine quadratische Gleichung der Form $ax^2+bx+c=0$ besitzt Nullstellen bei
$x_{1{,}2}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$
$u_{1}=\frac{30}{20}=\frac{3}{2}$
$u_{2}=-\frac{8}{20}=-\frac{2}{5}$
Wir erhalten die beiden Nullstellen $u_1$ und $u_2$ .
Normalform allgemein:
$f(x)=a \cdot x^2+b \cdot x+c$
Nullstellenform allgemein:
$f(x)=a \cdot (x-x_1) \cdot (x-x_2)$
Normalform hier:
$a \cdot u^2+b \cdot u+c$
Nullstellenform hier:
$a \cdot (u-u_1) \cdot (u-u_2)$
$a$ wird neben den gefundenen Nullstellen $u_1$ und $u_2$ in die Nullstellenformel eingesetzt.
$10\cdot(u-\frac{3}{2})\cdot(u-(-\frac{2}{5}))$
$10 \cdot (u- \frac{3}{2}) \cdot (u+\frac{2}{5})$
Günstige Umschreibung des Faktors und anschließendes Ausmultiplizieren.
$2 \cdot 5 \cdot (u- \frac{3}{2}) \cdot (u+\frac{2}{5})$
$2 \cdot (u- \frac{3}{2}) \cdot 5 \cdot (u+\frac{2}{5})$
$(2 \cdot u- 2 \cdot \frac{3}{2}) \cdot (5 \cdot u+ 5 \cdot \frac{2}{5})$
$(2u- 3) \cdot (5u+2)$
Der ursprüngliche Zähler wurde faktorisiert.
$(2u-3)\cdot(5u+2)=10u^2-11u-6$
$\frac{10u^2-11u-6}{(5u-2) \cdot (5u+2)}=\frac{(2u- 3) \cdot (5u+2)}{(5u-2) \cdot(5u+2)}=\frac{(2u- 3)}{(5u-2)}$
Der vereinfachte Term lautet $\frac{(2u-3)}{(5u-2)}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\dfrac{c^2+c-20}{-c^2+c+30}$

$\dfrac{7r^2s}{12\left(r-s\right)}\;\cdot\;\dfrac{(2\mathrm{sr}-2r)^2}{21\mathrm{rs}^2}$

$\dfrac{\left(\frac66a^2\right)^3:\left(\frac{4x}{y^2}\right)^2}{\frac1{\left(2a^2b\right)^3\cdot\left(3x^2y^3\right)^3}}\;:\;\dfrac{2a^3b}5$

$\dfrac{\frac23b^2+\left(\frac{3b}2\right)^2-\frac56b^2}{\left(\frac43a^2b\right)^3}\;:\;\dfrac{\left(\frac{2a}3\right)^2}{\frac{5a^3}{b^2}}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche kürzen und erweitern

Löse die Klammern mithilfe der Potenzgesetze auf.

$\displaystyle \dfrac{\frac23b^2+\left(\frac{3b}2\right)^2-\frac56b^2}{\left(\frac43a^2b\right)^3}\;:\;\dfrac{\left(\frac{2a}3\right)^2}{\frac{5a^3}{b^2}}$	$=$	$\displaystyle \dfrac{\frac23b^2+\frac{9b^2}4-\frac56b^2}{\frac{64}{27}a^6b^3}\;:\;\dfrac{\frac{4a^2}9}{\frac{5a^3}{b^2}}$
	↓	Multipliziere mit dem Kehrbruch.
$\displaystyle$	$=$	$\displaystyle \dfrac{b^2\cdot\left(\frac23+\frac94-\frac56\right)}{\frac{64}{27}a^6b^3}\;\cdot\dfrac{\frac{5a^3}{b^2}}{\frac{4a^2}9}$
	↓	Multipliziere die beiden Brüche und kürze im Zähler mit $b^2$ .
	$=$	$\displaystyle \dfrac{5a^3\cdot\left(\frac23+\frac94-\frac56\right)}{\frac{64}{27}a^6b^3\cdot\frac{4a^2}9}$
	↓	Bilde im Zähler den Hauptnenner (12) und erweitere alle Brüche auf diesen. Multipliziere im Nenner aus.
$\displaystyle$	$=$	$\displaystyle \dfrac{5a^3\cdot\left(\frac8{12}+\frac{27}{12}-\frac{10}{12}\right)}{\frac{256a^8b^3}{243}}$
	↓	Berechne das Innere der Klammer $\left(\frac{25}{12}\right)$ .
$\displaystyle$	$=$	$\displaystyle \dfrac{\frac{125a^3}{12}}{\frac{256a^8b^3}{243}}$
	↓	Der mittlere Bruchstrich entspricht einem "Geteilt", stattdessen kannst du deswegen mit dem Kehrbruch multiplizieren.
$\displaystyle$	$=$	$\displaystyle \dfrac{125a^3}{12}\cdot\dfrac{243}{256a^8b^3}$
	↓	Multipliziere und kürze mit $3a^3$ .
	$=$	$\displaystyle \dfrac{10125}{1024a^5b^3}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

2

Erweitere die folgenden Brüche entsprechend.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
$\frac{779a^3b^9}{703a^4b^4d^4}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
$\frac{153\left(a+b\right)^2\mathrm{abcd}}{255a^2b^2c^2d^2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

3

Bringe die folgenden Brüche jeweils auf den gleichen Nenner.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
Für jeden Term im Nenner wird das kgV bestimmt. Für die Formvariablen (hier f, g, h) werden die jeweils höchsten Potenzen ermittelt. Damit ist dann der Hauptnenner fertig. Der für jeden Zähler korrekte Erweiterungsfaktor kann dann ermittelt werden.
Das kgV $(48;112)$ wird ermittelt:
$48=16\cdot 3=2^4\cdot 3\\112=16\cdot 7=2^4\cdot 7$
Erkenntnis aus der Primfaktorzerlegung:
Bestimme für das kgV die höchste vorkommende Potenz aller Primfaktoren.
Primzahl $2$ hat die Vielfachheit $4$
Primzahl $3$ hat die Vielfachheit $1$
Primzahl $7$ hat die Vielfachheit $1$
Somit gilt: kgV $(48;112)$ $=2^4\cdot 3^1\cdot 7^1=336$
Für die Formvariablen (hier $f, g, h$ ) werden die jeweils höchsten Potenzen ermittelt:
$f$ hat die höchste Potenz $2$
$g$ hat die höchste Potenz $4$
$h$ hat die höchste Potenz $1$
$\;\Rightarrow\;f^2\cdot g^4\cdot h$
Der Hauptnenner ist demnach $336\cdot f^2\cdot g^4\cdot h$
Ermittlung des Erweiterungsfaktors und Durchführung der Erweiterung
Der Bruch $\dfrac{3fg^2}{48f^2g^4}$ muss mit $7\cdot h$ erweitert werden, denn $\dfrac{336\cdot f^2\cdot g^4\cdot h}{48\cdot f^2\cdot g^4}=7\cdot h$ .
$\;\Rightarrow\;\dfrac{3fg^2}{48f^2g^4}\cdot \dfrac{7h}{7h}=\dfrac{21\mathrm{fg}^2h}{336f^2g^4h}$
Der Bruch $\dfrac{2h^5}{112fgh}$ muss mit $3\cdot f\cdot g^3$ erweitert werden, denn $\dfrac{336\cdot f^2\cdot g^4\cdot h}{112\cdot f\cdot g\cdot h}=3\cdot f\cdot g^3$ .
$\;\Rightarrow\; \dfrac{2h^5}{336f^2g^4h}\cdot \dfrac{3\cdot f\cdot g^3}{3\cdot f\cdot g^3}=\dfrac{6\mathrm{fg}^3h^5}{336f^2g^4h}$
Der Bruch $\dfrac{8}{1}$ muss mit dem Hauptnenner $336\cdot f^2\cdot g^4\cdot h$ erweitert werden:
$\;\Rightarrow\;\dfrac{8}{1}\cdot \dfrac{336\cdot f^2\cdot g^4\cdot h}{336\cdot f^2\cdot g^4\cdot h}=\dfrac{2688f^2g^4h}{336f^2g^4h}$
Ergebnis:
$\dfrac{21\mathrm{fg}^2h}{336f^2g^4h};\;\;\;\;\dfrac{6\mathrm{fg}^3h^5}{336f^2g^4h};\;\;\;\;\dfrac{2688f^2g^4h}{336f^2g^4h}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für jeden Term im Nenner wird das kgV bestimmt.
Für die Formvariablen (hier f, g, h) werden die jeweils höchsten Potenzen ermittelt. Damit ist dann der Hauptnenner fertig.

4

Berechne den Term mit Unbekannten und kürze so weit wie möglich.

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

5

Der gut durchtrainierte Hobbyradrennfahrer Walter bewältigt einen 20 km langen Anstieg in 2,0 Stunden; seine Durchschnittsgeschwindigkeit dabei beträgt also $10\frac{\mathrm{km}}{\mathrm{h}}$ .

Oben angekommen dreht Walter sofort um und fährt die 20 km wieder zurück ins Tal.

Seine Durchschnittsgeschwindigkeit $\overline v$ für die Gesamtstrecke lässt sich mit dem Term

\displaystyle \frac{u}{2v}-\frac{v}{2u}

berechnen.

Kann Walter für die Gesamtstrecke eine Durchschnittsgeschwindigkeit von $20\frac{\mathrm{km}}{\mathrm{h}}$ erreichen?

Ja, Walter kann eine Durchschnittsgeschwindigkeit von $20\frac{\mathrm{km}}{\mathrm{h}}$ erreichen.
Nein, Walter kann eine Durchschnittsgeschwindigkeit von $20\frac{\mathrm{km}}{\mathrm{h}}$ nicht erreichen.

6

Fasse jeweils zu einem Bruch zusammen. In welchen Fällen ändert sich durch die Umformung die maximale Definitionsmenge?

$\dfrac2x-\dfrac x2+x$

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

$\frac{a-3}{a^2-3a}\cdot\frac{2a}{a+3}$

$1-\frac{x-3}{x+2}:\frac{3-x}{x+2}$

7

Vereinfache so weit wie möglich.

$2x:\frac4x$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche multiplizieren
$\frac{2x}{\left(\frac{4}{x}\right)}=\frac{2x^2}{4}=\frac{x^2}{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$2-\frac{2x}{x-1}$

$\frac{6+2z}{z^2+6z+9}$

$\frac3{z+3}-\frac3{z-3}$

8

Multipliziere die folgenden Brüche.

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

9

Dividiere die folgenden Brüche.

$\dfrac{9c}{10ab}\;:\;\dfrac{6ac}{25b}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Division von Brüchen
$\def\arraystretch{2} \begin{array}{rcll} \dfrac{9c}{10\mathrm{ab}}\;:\;\dfrac{6\mathrm{ac}}{25b} &=& \dfrac{9c}{10ab}\;\cdot\;\dfrac{25b}{6ac} \\\\ &=&\dfrac{(9c)\cdot(25b)}{(10ab)\cdot(6ac)} \\\\ &=& \dfrac{225cb}{60a^2bc} &\vert \text{Kürze } cb \text{ und } bc \\\\ &=& \dfrac{225}{60a^2} &\vert \text{Kürze mit} 15 \\\\ &=& \dfrac{15}{4a^2} \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\dfrac{\left(2uv^2\right)^3}{18w^4}\;:\;\dfrac{4uv^4}{\left(3uw\right)^2}$

10

Kürze vollständig.

$\dfrac{2x+4x}4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche kürzen
Addiere im Zähler
$\displaystyle \frac{2x+4x}{4}$ $=$ $\displaystyle \frac{6x}{4}$
↓
Dividiere durch den gemeinsamen Teiler 2.
$=$ $\displaystyle \frac{3x}{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\dfrac{6f^4(gh)^5}{(2fg)^3h^2}$

$\dfrac{x^4-2x^3-15x^2+32x-16}{x^3-3x^2+3x-1}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Faktorisieren

Faktorisiere den Nenner durch Ermittlung der Nullstellen.

Rate die erste Nullstelle. Kandidat $x=1$

$\displaystyle \textstyle x^3-3x^2+3x-1$	$=$	$\displaystyle \textstyle1^3-3\cdot1^2+3\cdot1-1$
	$=$	$\displaystyle 1-3+3-1$
	$=$	$\displaystyle 0$
	↓	Polynomdivision durch $x-1$ .
$\displaystyle (x^3-3x^2+3x-1):(x-1)$	$=$	$\displaystyle x^2-2x+1$
	↓	Berechne weitere Nullstellen
$\displaystyle x^2-2x+1$	$=$	$\displaystyle 0$
	↓	Binomische Formel
$\displaystyle (x-1)^2$	$=$	$\displaystyle 0$
$\displaystyle x_1=x_2$	$=$	$\displaystyle 1$
$\displaystyle \textstyle x^3-3x^2+3x-1$	$=$	$\displaystyle \left(x-1\right)^3$

Zähler faktorisieren

Rate die erste Nullstelle. Kandidat $x=1$

$\displaystyle x^4-2x^3-15x^2+32x-16$	$=$	$\displaystyle \textstyle1^4-2\cdot1^3-15\cdot1^2+32\cdot1-16$
	$=$	$\displaystyle 1-2-15+32-16$
	$=$	$\displaystyle 0$
	↓	Polynomdivision durch $x-1$ .
$\displaystyle \left(x^4-2x^3-15x^2+32x-16\right):\left(x-1\right)$	$=$	$\displaystyle \left(x^3-x^2-16x+16\right)$
	↓	Rate weitere Nullstelle. Kandidat wieder $x=1$ .
$\displaystyle 1^3-1^2-16\cdot1+16$	$=$	$\displaystyle 0$
	↓	Polynomdivision durch $x-1$ .
$\displaystyle \left(x^3-x^2-16x+16\right):\left(x-1\right)$	$=$	$\displaystyle x^2-16$
	↓	Berechne weitere Nullstellen.
$\displaystyle x$	$=$	$\displaystyle \pm4$
$\displaystyle x^4-2x^3-15x^2+32x-16$	$=$	$\displaystyle \left(x-1\right)^2\cdot\left(x+4\right)\cdot\left(x-4\right)$

Zähler durch Nenner dürch Kürzen vereinfachen

$\displaystyle \frac{x^4-2x^3-15x^2+32x-16}{x^3-3x^2+3x-1}=\frac{(x-1)^2(x+4)(x-4)}{(x-1)^3}=\frac{(x+4)(x-4)}{(x-1)}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

11

Vereinfache:

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

12

Bringe auf einen Bruchstrich: $\frac1{R_1}+\frac1{R_2}+\frac1{R_1+R_2}$

13

Vereinfache:

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

14

Vereinfache:

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

15

Vereinfache:

$\dfrac{\;\;\displaystyle\frac JC\;\;}J$

$\dfrac J{\;\displaystyle\frac JC\;}$

$\dfrac{\;{\displaystyle\frac1{x^2}}-2\;}{1-\displaystyle\frac1x}$

16

Bestimme die Definitionsmenge:

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Der Nenner muss immer ungleich null sein.
Setze den Nenner gleich null:
$\displaystyle 36x^2-16x$ $=$ $\displaystyle 0$
↓
Klammere $4x$ aus.
$\displaystyle 4x\cdot(9x-4)$ $=$ $\displaystyle 0$
Du hast die Gleichung $4x\cdot(9x-4)=0$ erhalten. Wende nun den Satz vom Nullprodukt an.
$4x=0$ oder $9x-4=0\;\Rightarrow\;x=0\;\text{oder} \;x=\dfrac{4}{9}$
Somit ergibt sich die Definitionsmenge zu $\mathbb D=\mathbb R\backslash\{0; \frac{4}{9}\}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Nenner muss immer ungleich null sein.
Berechne also, für welchen x-Wert der Nenner null wird.

\displaystyle \frac{u}{2v}-\frac{v}{2u}

17

Benutze binomische Formeln um die Brüche zu kürzen

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

\displaystyle \frac{u}{2v}-\frac{v}{2u}

18

Vereinfache folgende Funktionen so weit wie möglich, indem du die binomischen Formel anwendest.

$\displaystyle f(x)= \frac{(x+1)\cdot (x-1)+1}{x^3}$

$g(z)=\dfrac{(z+3)^2-6z-9}{3z^3}$

$\displaystyle h(t)= \frac{t^2-8t+16}{2(t-4)}$

19

Vereinfache die Funktionen, indem du die Brüche auf einen gemeinsamen Nenner bringst.

$\displaystyle f(x)= \frac {5x}{4}+\frac{1}{2}$

$\displaystyle g(x)= \frac{6}{x}-\frac{2}{3x^2}$

$\displaystyle h(x)= \frac{1}{(x+1)}-\frac{x}{(x+1)^2}$

20

Vereinfache die Funktion durch Ausklammern und Kürzen.

$\displaystyle f(x)= \frac{4x^2+2x}{2x^2(2x+1)}$

$\displaystyle g(x)= \frac{2x^2-2}{6}$

$\displaystyle h(x)= \frac{12x^3+4x}{4x^2+8x}$

21

Kürze die Bruchterme so weit wie möglich.

Dazu kann es notwendig sein, im Zähler oder im Nenner einen Faktor auszuklammern!

Kürze den Bruchterm so weit wie möglich!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
$\frac{63x}{14xy}=\frac{ \color{ff6600}{7} \color{#000000}{ \cdot 9\cdot} \color{ff6600}{x}}{ \color{ff6600}{7} \color{#000000}{\cdot2\cdot \color{ff6600}{x} \color{#000000}{ \cdot y}}}$
Kürzen der gleichen Faktoren:
$=\frac{9}{2y}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Finde Teiler, durch die sich Zähler und Nenner kürzen lassen.
Kürze den Bruchterm so weit wie möglich!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
Klammere zunächst jeweils im Zähler und im Nenner alle gleichen Faktoren aus.
Kürze nun gleiche Faktoren.
Die Klammer $(x+4)$ ist ebenfalls ein gleicher Faktor in Zähler und Nenner.
Der Bruch lässt sich nicht weiter kürzen. Dies ist also der vollständig gekürzte Bruch.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Finde Teiler, durch die sich Zähler und Nenner kürzen lassen.
Kürze den Bruchterm so weit wie möglich!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
Klammere zunächst im Zähler und Nenner alle gleichen Faktoren aus.
In allen Summanden im Zähler kommt ein x und eine 8 vor. In allen Summanden im Nenner kommt ein x und eine 8 vor:
Jetzt lässt sich der Faktor $8x$ kürzen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Finde Teiler, durch die sich Zähler und Nenner kürzen lassen.

22

Kürze so weit wie möglich.

Gib dein Ergebnis ins Eingabefeld in der Form zähler/nenner ein. Malpunkte können dabei weggelassen werden.

$\frac{28x}{36x^2}$

(Form: z/n)

$\frac{x}{7x}$
(Form: z/n)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme kürzen
Die Zahlen lassen sich nicht weiter in kleinere Faktoren zerlegen. Deshalb kannst du direkt streichen:
$\displaystyle \frac{x}{7x}$ $=$ $\displaystyle \frac{\cancel{x}\cdot 1}{7\cdot \cancel{x} }$
↓
Im Zähler bleibt eine 1!
$=$ $\displaystyle \frac{1}{7}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zerlege die Zahlen in Primfaktoren und schreibe die Variable ohne Exponent.

$\frac{105x^2y}{350xy^2}$

(Form: z/n)

23

Vereinfache beide Terme soweit wie möglich, falls dies möglich ist.

$\frac{9x}{3x-6x^2}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gebrochen-rationale Funktionen
Klammere zuerst 3 $x$ aus.
$\displaystyle \frac{9x}{3x-6x^2}$ $=$ $\displaystyle =\frac{9x}{3x\;(1-2x)}$
↓
Kürze 3 $x$
$=$ $\displaystyle =\frac3{1-2x}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$\frac{4}{4+x^2}$
Begründe, dass die Termwerte von b) nicht größer als 1 werden können, unabhängig davon, welche Zahl man für $x$ einsetzt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gebrochen-rationale Funktionen
$\;\;\Rightarrow\;\;$ keine Vereinfachung möglich
Warum können die Termwerte von Teilaufgabe b) nie größer als 1 werden?
Egal welche Zahl man für $x$ einsetzt, $x^2$ ist immer positiv. Das heißt also, dass $4+x^2 \geq4$ . Damit ist im Bruch $\frac4{4+x^2}$ der Zähler immer kleiner gleich dem Nenner und der Bruch kann somit nie größer als $1$ werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

24

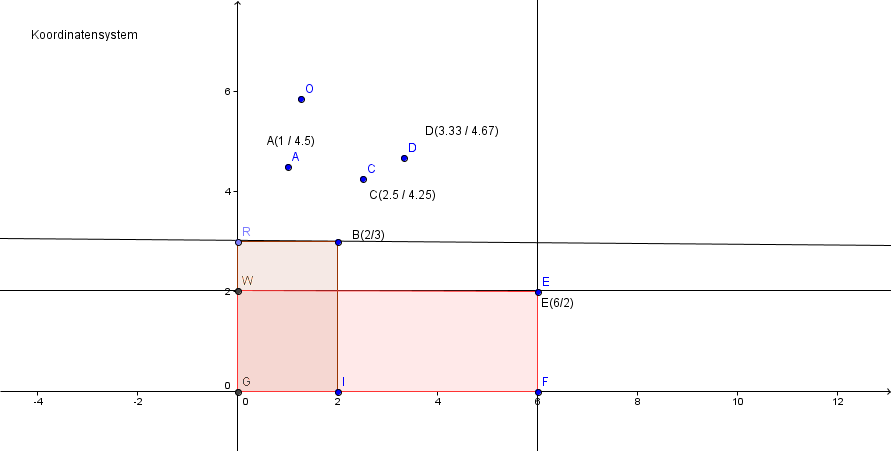
Gegeben ist der Term $T\left(x\right)=-\frac{1}{2}x+5$ . Setze für $x$ die Werte $1 ; 2 ; 2{,}5 ;$ $3\frac{1}{3}$ $; 6 ; 8$ ein und trage die Termwerte in einer Tabelle zusammen. Der Tabelle kannst du Wertepaare $(x | T(x) )$ , z. B. $(2 | T(2) )$ , entnehmen und als Koordinaten des Punktes $(2|4)$ deuten.

Trage für die Wertepaare aus der Tabelle die zugehörigen Punkte in ein Koordinatensystem ein.

Tabelle
$1$
$2$
$2{,}5$
$3\frac13$
$6$
$8$
$T(x)=-\frac12 x+5$
$4{,}5$
$4$
$4\frac14$
$4\frac23$
$2$
$1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Zeichne vom Punkt $(2 | T(2) )$ die Lote auf die $x$ - und $y$ -Achse; es entsteht ein Rechteck. Zeichne auch für den Punkt $(6 | T(6))$ das entsprechende Rechteck ein. Suche den Wert für $x$ , bei dem das zu $(x | T(x))$ gehörende Rechteck einen möglichst großen Flächeninhalt hat.

25

Gegeben ist der Term $T\left(x\right)=\dfrac{5-2x}{x-3}$ .

Erstelle eine Tabelle für die Werte von $x$ und $T(x)$ . Setze für $x$ die folgenden Werte in die Tabelle ein: $-4{,}5$ ; $-4$ ; $-\frac32$ ; $0$ ; $1$ ; $2\frac12$ ; $3\frac13$ ; $4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Term

Setze in $T(x) =\dfrac{5-2x}{x-3}$ die Werte

$x=-4{,}5$
$x=-4$
$x=-\frac{3}{2}$
$x=0$
$x=1$
$x=2\frac{1}{2}$
$x=3\frac{1}{3}$
$x=4$

ein.

$x$	$-4{,}5$	$-4$	$-\frac{3}{2}$	$0$	$1$	$2\frac{1}{2}$	$3\frac{1}{3}$	$4$
$T\left(x\right)$	$-\frac{28}{15}$	$-\frac{13}{7}$	$-\frac{16}{9}$	$-\frac{5}{3}$	$-\frac{3}{2}$	$0$	$-5$	$-3$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Beschreibe, was für ein Problem an der Stelle $x=3$ auftritt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Term
$T\left(x\right)=\frac{5-2x}{x-3}$
Wenn du $x=3$ in den Term $T(x)$ einsetzt, erhältst du den Nenner $3-3 =0$ . Da jedoch nie durch $0$ geteilt werden darf, ist der Term $T(x)_{ }$ für $x=3$ nicht definiert.
Der Term $T(x)$ hat also eine Defintionslücke an der Stelle $x=3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

26

Bruchterme

Ordne den Bruchtermen ihren Definitionsbereich zu.
Welcher Term beschreibt den Hauptnenner von: $\dfrac{3}{x+1}\quad\text{und}\quad\dfrac{1}{x^2+x}$
- $(x+1)^2$
- $x+1$
- $x(x+1)$

$\displaystyle \frac{a+b}{b}-\frac{a-b}{a}$	$=$	$\displaystyle \frac{\left(a+b\right)\cdot a}{b\cdot a}-\frac{\left(a-b\right)\cdot b}{a\cdot b}$
	↓	Fasse die beiden Brüche zu einen zusammen.
	$=$	$\displaystyle \frac{(a+b)\cdot a-(a-b)\cdot b}{b\cdot a}$
	↓	Multipliziere aus.
	$=$	$\displaystyle \frac{a^2+ab-ab+b^2}{b\cdot a}$
	↓	Berechne im Zähler $ab-ab$ .
	$=$	$\displaystyle \frac{a^2+b^2}{b\cdot a}$

	$\displaystyle \displaystyle\frac{\left(\frac{6}{6}a^2\right)^3:\left(\frac{4x}{y^2}\right)}{\displaystyle\frac{1}{\left(2a^2b\right)^3\cdot\left(3x^2y^3\right)^3}}:\frac{2a^3b}{5}$
	↓ Löse die Klammern mithilfe der Potenzgesetze auf
$=$	$\displaystyle \displaystyle\frac{a^6:\frac{16x^2}{y^4}}{\displaystyle\frac{1}{8a^6b^3\cdot27x^6y^9}}:\frac{2a^3b}{5}$
	↓ Multipliziere im Zähler des ersten Bruchs mit dem Kehrbruch
$=$	$\displaystyle \displaystyle\frac{\displaystyle\frac{a^6y^4}{16x^2}}{\displaystyle\frac{1}{216a^6b^3x^6y^9}}:\frac{2a^3b}{5}$
	↓ Der mittlere Bruchstrich entspricht einem "Geteilt", deshalb kannst du stattdessen mit dem Kehrbruch multiplizieren. Gleiches bei dem zweiten Bruch.
$=$	$\displaystyle \displaystyle\frac{a^6y^4}{16x^2}\cdot\frac{216a^6b^3x^6y^9}{1}\cdot\frac{5}{2a^3b}$
	↓ Kürze mit $8a^3bx^2$ .
$=$	$\displaystyle \displaystyle\frac{a^6y^4}{2}\cdot\frac{27a^3b^2x^4y^9}{1}\cdot\frac{5}{2}$
	↓ Multipliziere.
$=$	$\displaystyle \displaystyle\frac{135}{4}a^9b^2x^4y^{13}$

$\displaystyle \dfrac u{2v}-\dfrac v{2u}$	$=$	$\displaystyle \dfrac{u\cdot u}{2vu}-\dfrac{v\cdot v}{2uv}$
	↓	Schreibe auf gemeinsamen Bruchstrich
	$=$	$\displaystyle \dfrac{u^2-v^2}{2uv}$

$\displaystyle \dfrac{13}{6h^2}+1-\dfrac4{21h}$	$=$	$\displaystyle \dfrac{13\cdot7}{6h^2\cdot7}+\dfrac{1\cdot42h^2}{1\cdot42h^2}-\dfrac{4\cdot2h}{21h\cdot2h}$
	↓	Multipliziere aus.
	$=$	$\displaystyle \dfrac{91}{42h^2}+\dfrac{42h^2}{42h^2}-\dfrac{8h}{42h^2}$
	↓	Schreibe die Brüche auf einen gemeinsamen Bruchstrich.
	$=$	$\displaystyle \dfrac{42h^2-8h+91}{42h^2}$

$\displaystyle \overline{v}_{Ges}$	$=$	$\displaystyle \frac{40\ \text{km}}{2{,}0\ \text{h}+t_{ }}$
	↓	Setze $\;{\overline v}_\mathrm{Ges}=20\frac{\mathrm{km}}{\mathrm{h}}$ ein.
$\displaystyle 20\ \frac{\text{km}}{\text{h}}$	$=$	$\displaystyle \frac{40\ \text{km}\ }{2{,}0\ \text{h}+\ t_{\text{Tal}}}$	$\displaystyle \cdot\ \left(2{,}0\text{h}+t_{ }\right)$
$\displaystyle 20\ \frac{\text{km}}{\text{h}}\cdot\left(2{,}0\text{h}+t_{\text{Tal}}\right)$	$=$	$\displaystyle 40\ \text{km}\$	$\displaystyle :20\ \frac{\text{km}}{\text{h}}$
$\displaystyle 2{,}0\text{h}+t_{\text{Tal}}$	$=$	$\displaystyle \frac{40\text{km}\ }{20\ \frac{\text{km}\ }{\text{h}\ }}$
$\displaystyle 2{,}0\ \text{h}+t_{\text{Tal}}$	$=$	$\displaystyle 2{,}0\text{h}\$	$\displaystyle -2{,}0\ \text{h}\$
$\displaystyle t_{\text{Tal}\ }$	$=$	$\displaystyle 0\text{h}\$

$\displaystyle \frac{c}{c^2-8c+16}-\frac{2}{c^2-6c+8}$	$=$
	↓	Wende die 2. binomische Formel und den Satz von Vieta an
	$=$	$\displaystyle \frac{c}{\left(c-4\right)^2}-\frac{2}{\left(c-4\right)\left(c-2\right)}$
	↓	Bilde den Hauptnenner $((c-4)^2(c-2))$
	$=$	$\displaystyle \frac{c(c-2)-\left[2(c-4)\right]}{(c-4)^2(c-2)}$
	$=$	$\displaystyle \frac{c^2-2c-\left[2c-8\right]}{(c-4)^2(c-2)}$
	$=$	$\displaystyle \frac{c^2-2c-2c+8}{(c-4)^2(c-2)}$
	↓	Subtraktion
	$=$	$\displaystyle \frac{c^2-4c+8}{(c-2)(c-4)^2}$

$\displaystyle \frac{b-c}{a^2+ac}-\frac{a-b}{ac+c^2}+\frac{a^2+c^2}{a^2c+ac^2}$	$=$
	↓	Mache die Nenner übersichtlicher, um den Hauptnenner leichter zu finden.
	$=$	$\displaystyle \frac{b-c}{a\cdot(a+c)}-\frac{a-b}{c\cdot(a+c)}+\frac{a^2+c^2}{a\cdot c\cdot(a+c)}$
	↓	Bilde den Hauptnenner $(a \cdot c \cdot (a+c))$ und erweitere beide Brüche auf diesen.
	$=$	$\displaystyle \frac{c\cdot(b-c)}{a\cdot c\cdot(a+c)}-\frac{a\cdot(a-b)}{a\cdot c\cdot(a+c)}+\frac{a^2+c^2}{a\cdot c\cdot(a+c)}$
	↓	Schreibe den Term auf einen Bruchstrich
	$=$	$\displaystyle \frac{c\cdot(b-c)-a\cdot(a-b)+a^2+c^2}{a\cdot c\cdot(a+c)}$
	↓	Vereinfache den Zähler
	$=$	$\displaystyle \frac{bc-c^2-a^2+ab+a^2+c^2}{a\cdot c\cdot(a+c)}$
	$=$	$\displaystyle \frac{bc+ab}{a\cdot c\cdot(a+c)}$
	$=$	$\displaystyle \frac{b\left(a+c\right)}{a\cdot c\cdot(a+c)}$
	↓	Kürze $\left(a+c\right)$
	$=$	$\displaystyle \frac{b}{ac}$

$\displaystyle \frac{c^2+c-20}{-c^2+c+30}$	$=$
	$=$	$\displaystyle \frac{(c-4)\cdot(c+5)}{(c+5)\cdot(-c+6)}$
	$=$	$\displaystyle \frac{c-4}{-c+6}$
	$=$	$\displaystyle -\frac{c-4}{c-6}$

$\displaystyle \frac{7r^2s}{12\left(r-s\right)}\cdot\frac{\left(2sr-2r\right)^2}{21rs^2}$	$=$
	↓	Kürze zunächst alles, was man schonmal kürzen kann. Hier die $7$ mit der $21$ , $r^2$ mit $r$ und $s$ mit $s^2$ .
	$=$	$\displaystyle \frac{r}{12\left(r-s\right)}\cdot\frac{\left(2sr-2r\right)^2}{3s}$
	↓	Nun kannst du in der Klammer $(2sr-2r)^2$ die $2r$ ausklammern.
	$=$	$\displaystyle \frac{r}{12\left(r-s\right)}\cdot\frac{\left(2r\left(s-1\right)\right)^2}{3s}$
	↓	Löse nun die Klammer oben mithilfe der Potenzgesetze auf.
	$=$	$\displaystyle \frac{r}{12\left(r-s\right)}\cdot\frac{4r^2\left(s-1\right)^2}{3s}$
	↓	Kürze die $4$ mit der $12$ und fasse zusammen
	$=$	$\displaystyle \frac{r3\left(s-1\right)^2}{9s\left(r-s\right)}$

$\displaystyle \frac{2}{x}$	$=$	$\displaystyle \frac{x}{2}+x$
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{0\right\}$
	↓	Zusammenfassung zu einem Bruch
$\displaystyle \frac{2}{x}-\frac{x}{2}+x$	$=$
	↓	Bilde den Hauptnenner
	$=$	$\displaystyle \frac{4}{2x}-\frac{x^2}{2x}+\frac{2x^2}{2x}$
	$=$	$\displaystyle \frac{x^2+4}{2x}$
	↓	Neue Definitionsmenge bestimmen
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{0\right\}$

$\displaystyle 1-\frac{2-y}{y}$	$=$
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{0\right\}$
	↓	Zusammenfassen zu einem Bruch; den Hauptnenner bilden
	$=$	$\displaystyle \frac{y-\left(2-y\right)}{y}$
	$=$	$\displaystyle \frac{y-2+y}{y}$
	$=$	$\displaystyle \frac{2y-2}{y}$

$\displaystyle \frac{x}{x-x^2}-\frac{3}{1-x}$	$=$
	↓	Klammere $x$ aus
	$=$	$\displaystyle \frac{x}{x\cdot\left(1-x\right)}-\frac{3}{1-x}$
	↓	Lese die Definitionslücken ab.
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{1;0\right\}$
	↓	Bruch berechnen
$\displaystyle \frac{x}{x\cdot\left(1-x\right)}-\frac{3}{1-x}$	$=$
	↓	Kürze mit $x$
	$=$	$\displaystyle \frac{1}{1-x}-\frac{3}{1-x}$
	↓	Subtrahiere die Brüche
	$=$	$\displaystyle -\frac{2}{1-x}$
	↓	Lese die Definitionslücke ab
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{1\right\}$

$\displaystyle \frac{t}{t-a}+\frac{2}{t}+1$	$=$
	↓	Bilde den Hauptnenner $t\cdot\left(t-a\right)$ und erweitere alle Brüche auf diesen
	$=$	$\displaystyle \frac{t\cdot t}{t\cdot\left(t-a\right)}+\frac{2\cdot\left(t-a\right)}{t\cdot\left(t-a\right)}+\frac{t\cdot\left(t-a\right)}{t\cdot\left(t-a\right)}$
	↓	Addiere
	$=$	$\displaystyle \frac{t^2+2\cdot\left(t-a\right)+t\cdot\left(t-a\right)}{t\cdot\left(t-a\right)}$
	↓	Multipliziere im Zähler die Klammern aus und fasse zusammen
	$=$	$\displaystyle \frac{2t^2+2t-2a-at}{t\cdot\left(t-a\right)}$

$\displaystyle \frac{a-3}{a^2-3a}\cdot\frac{2a}{a+3}$	$=$
	↓	a ausklammern
	$=$	$\displaystyle \frac{a-3}{a\cdot\left(a-3\right)}\cdot\frac{2a}{a+3}$
	↓	Definitionslücken ablesen
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{-3;\ 0;\ 3\right\}$
	↓	Zusammenfassen zu einem Bruch
$\displaystyle \frac{a-3}{a\cdot\left(a-3\right)}\cdot\frac{2a}{a+3}$	$=$	$\displaystyle \frac{\left(a-3\right)\cdot2a}{a\cdot\left(a-3\right)\cdot\left(a+3\right)}$
	↓	Bruch mit $a\cdot\left(a-3\right)$ kürzen
	$=$	$\displaystyle \frac{2}{a+3}$
	↓	neue Definitionsmenge bestimmt
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{-3\right\}$

$\displaystyle 1-\frac{x-3}{x+2}:\ \frac{3-x}{x+2}$	$=$
	↓	mit dem Kehrwert multiplizieren
	$=$	$\displaystyle 1-\frac{x-3}{x+2}\cdot\frac{x+2}{3-x}$
	↓	Definitionsbereich ablesen
$\displaystyle D_f$	$=$	$\displaystyle ℝ\backslash\left\{-2;\ 3\right\}$
	↓	Zusammenfassen zu einem Bruch
$\displaystyle 1-\frac{x-3}{x+2}:\ \frac{3-x}{x+2}$	$=$
	↓	mit dem Kehrwert multiplizieren
	$=$	$\displaystyle 1-\frac{x-3}{x+2}\cdot\frac{x+2}{3-x}$
	↓	$(x+2)$ kürzen
	$=$	$\displaystyle 1-\frac{x-3}{3-x}$
	↓	-1 im Zähler ausklammern
	$=$	$\displaystyle 1-\frac{-\left(3-x\right)}{3-x}$
	↓	$(3-x)$ kürzen
	$=$	$\displaystyle 1-\left(-1\right)$
	$=$	$\displaystyle 2$
	↓	Neue Definitionsmenge bestimmen/ablesen
$\displaystyle D_f$	$=$	$\displaystyle ℝ$

$\displaystyle 2-\frac{2x}{x-1}$	$=$	$\displaystyle \frac{2\left(x-1\right)}{\;\;x-1}-\frac{2x}{x-1}$
	↓	Zusammenfassen
	$=$	$\displaystyle \frac{2x-2-2x}{x-1}$
	$=$	$\displaystyle \frac{-2}{x-1}$
	↓	(ggf. zur besseren Anschauung)
	$=$	$\displaystyle -\frac{2}{x-1}$

$\displaystyle \frac{6+2z}{z^2+6z+9}$	$=$
	↓	Wende eine binomische Formel an.
	$=$	$\displaystyle \frac{6+2z}{\left(z+3\right)^2}$
	↓	Im Zähler die $2$ ausklammern.
	$=$	$\displaystyle \frac{2\left(3+z\right)}{\left(z+3\right)^2}$
	↓	Kürze mit $(z+3)$ .
	$=$	$\displaystyle \frac{2}{z+3}$

$\displaystyle \frac{3}{z+3}-\frac{3}{z-3}$	$=$
	↓	Hauptnennerbildung und Brüche mit diesem erweitern.
	$=$	$\displaystyle \frac{3\cdot\left(z-3\right)}{\left(z+3\right)\left(z-3\right)}-\frac{3\cdot\left(z+3\right)}{\left(z-3\right)\left(z+3\right)}$
	↓	Ausmultiplizieren.
	$=$	$\displaystyle \frac{3z-9}{\left(z+3\right)\left(z-3\right)}-\frac{3z+9}{\left(z+3\right)\left(z-3\right)}$
	↓	Zusammenfassen.
	$=$	$\displaystyle \frac{3z-9-\left(3z+9\right)}{\left(z+3\right)\left(z-3\right)}$
	↓	Klammer im Zähler auflösen.
	$=$	$\displaystyle \frac{3z-9-3z-9}{\left(z+3\right)\left(z-3\right)}$
	↓	Zähler zusammenfassen.
	$=$	$\displaystyle \frac{-18}{\left(z+3\right)\left(z-3\right)}$

$\displaystyle \frac{17r^4s^324st^2}{54t^585r^2}$	$=$
	↓	Klammere $r^2$ aus.
	$=$	$\displaystyle \frac{r^2(17r^2s^324st^2)}{54t^585r^2}$
	↓	Kürze mit $r^2$ .
	$=$	$\displaystyle \frac{17r^2s^324st^2}{54t^585}$
	↓	Kürze mit $t^2$ .
	$=$	$\displaystyle \frac{17r^2s^324s}{54t^385}$
	↓	Multipliziere.
	$=$	$\displaystyle \frac{408r^2s^4}{4590t^3}$	$\displaystyle :102$
	$=$	$\displaystyle \frac{4r^2s^4}{45t^3}$

$\displaystyle \frac{7m^2}{12n^3}\cdot\left(\frac{3n^2}{7m}\right)^2$	$=$
	↓	Quadriere den rechten Bruch.
	$=$	$\displaystyle \frac{7m^29n^4}{12n^349m^2}$
	↓	Kürze mit $m^2$ .
	$=$	$\displaystyle \frac{7\cdot9n^4}{12n^3\cdot49}$
	↓	Kürze mit 7.
	$=$	$\displaystyle \frac{9n^4}{12n^3\cdot7}$
	↓	Kürze mit $n^3$ .
	$=$	$\displaystyle \frac{9n}{12\cdot7}$
	↓	Kürze mit 3.
	$=$	$\displaystyle \frac{3n}{28}$

$\displaystyle T(u,v,w)$	$=$	$\displaystyle \dfrac{(2uv^2)^3}{18w^4}\cdot\dfrac{(3uw)^2}{4uv^4}$
	↓	Berechne die Potenzen.
	$=$	$\displaystyle \dfrac{2^3u^3v^6}{18w^4}\cdot\dfrac{3^2u^2w^2}{4uv^4}$
	↓	Schreibe $18$ als $2\cdot3^2$ und $4$ als $2^2$
	$=$	$\displaystyle \dfrac{2^3u^3v^6}{2\cdot3^2w^4}\cdot\dfrac{3^2u^2w^2}{2^2uv^4}$
	↓	Kürze die Potenzen mit der $2$ und die Potenzen mit der $3$ .
	$=$	$\displaystyle \dfrac{u^3v^6}{w^4}\cdot\dfrac{u^2w^2}{uv^4}$
	↓	Fasse zusammen.
	$=$	$\displaystyle \dfrac{u^5v^6w^2}{w^4uv^4}$
	↓	Kürze die Potenzen.
	$=$	$\displaystyle \dfrac{u^4v^2}{w^2}$

$\displaystyle \frac{2x+4x}{4}$	$=$	$\displaystyle \frac{6x}{4}$
	↓	Dividiere durch den gemeinsamen Teiler 2.
	$=$	$\displaystyle \frac{3x}{2}$

$\displaystyle \frac{6f^4(gh)^5}{(2fg)^3h^2}$	$=$	$\displaystyle \frac{6f^4g^5h^5}{8f^3g^3h^2}$
	↓	Kürze mit $2f^3g^3h^2$ .
	$=$	$\displaystyle \frac{3fg^2h^3}{4}$

$\displaystyle \frac{45x-20}{36x^2-16x}$	$=$	$\displaystyle \frac{5\cdot9\cdot x-5\cdot4}{4\cdot9\cdot x^2-4\cdot4\cdot x}$
	↓	Klammere im Zähler $5$ und im Nenner $4x$ aus.
	$=$	$\displaystyle \frac{5\left(9x-4\right)}{4x\left(9x-4\right)}$
	↓	Kürze $(9x-4)$ aus Zähler und Nenner.
	$=$	$\displaystyle \frac{5}{4x}$

$\displaystyle \frac{\left(ab\right)^2}{a^3b-a^2b^3}$	$=$	$\displaystyle \frac{a^2b^2}{a^2b\left(a-b^2\right)}$
	↓	Kürze $\mathrm a^2\mathrm b$ .
	$=$	$\displaystyle \frac b{a-b^2}$

Aufgaben zum Umgang mit Bruchtermen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nenner vereinfachen

Zähler seperat faktorisieren

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Das kgV(48;112)(48;112)(48;112) wird ermittelt:

Für die Formvariablen (hier f,g,hf, g, hf,g,h) werden die jeweils höchsten Potenzen ermittelt:

Ermittlung des Erweiterungsfaktors und Durchführung der Erweiterung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gebrochen-rationale Funktionen

Hast du eine Frage oder Feedback?

Neue Definitionsmenge bestimmen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Faktorisiere den Nenner durch Ermittlung der Nullstellen.

Zähler faktorisieren

Zähler durch Nenner dürch Kürzen vereinfachen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Tabelle

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Das kgV $(48;112)$ wird ermittelt:

Für die Formvariablen (hier $f, g, h$ ) werden die jeweils höchsten Potenzen ermittelt:

$\displaystyle \frac{1}{x-1}-\frac{1}{x+2}$	$=$	$\displaystyle \frac{x+2}{\left(x-1\right)\left(x+2\right)}-\frac{x-1}{\left(x-1\right)\left(x+2\right)}$
	↓	Subtrahiere.
	$=$	$\displaystyle \frac{x+2-\left(x-1\right)}{\left(x-1\right)\left(x+2\right)}$
	↓	Löse die Klammer auf.
	$=$	$\displaystyle \frac{3}{\left(x-1\right)\left(x+2\right)}$

$\displaystyle \frac{24-x}{x+3}-8$	$=$	$\displaystyle \frac{24-x}{x+3}-\frac{8(x+3)}{x+3}$
	↓	Klammern ausmultiplizieren.
	$=$	$\displaystyle \frac{24-x-8x-24}{x+3}$
	↓	Subtraktion
	$=$	$\displaystyle \frac{-9x}{x+3}$

	$\displaystyle \frac{6x^2+5}{36x^2-16x}+\frac{3x}{8-18x}$
	↓ Ausklammern in den Nennern. Es gilt $8-18x=-2\left(9x-4\right)$
$=$	$\displaystyle \frac{6x^2+5}{4x\left(9x-4\right)}+\frac{3x}{-2\left(9x-4\right)}$
	↓ Das Rechenzeichen hat sich wegen dem " $-$ " im zweiten Nenner geändert.
$=$	$\displaystyle \frac{6x^2+5}{4x\left(9x-4\right)}-\frac{3x}{2\left(9x-4\right)}$
	↓ Erweitere auf den Hauptnenner $4x\cdot(9x-4)$ .
$=$	$\displaystyle \frac{6x^2+5}{4x\left(9x-4\right)}-\frac{3x2x}{4x\left(9x-4\right)}$
	↓ Subtrahiere.
$=$	$\displaystyle \frac{6x^2+5-6x^2}{4x\left(9x-4\right)}$
$=$	$\displaystyle \frac{5}{4x\left(9x-4\right)}$

$\displaystyle \frac{6x+11}{2x+4}-\frac{2x+5}{x^2+2x}-3$	$=$	$\displaystyle \frac{6x+11}{2\left(x+2\right)}-\frac{2x+5}{x\left(x+2\right)}-3$
	↓	Erweitere auf den Hauptnenner $2x(x+2)$ .
	$=$	$\displaystyle \frac{\left(6x+11\right)x}{2x\left(x+2\right)}-\frac{\left(2x+5\right)\cdot2}{2x\left(x+2\right)}-\frac{3\cdot2x\left(x+2\right)}{2x\left(x+2\right)}$
	↓	Subtrahiere.
	$=$	$\displaystyle \frac{6x^2+11x-\left(4x+10\right)-\left(6x^2+12x\right)}{2x\left(x+2\right)}$
	↓	Löse die Klammern auf.
	$=$	$\displaystyle \frac{6x^2+11x-4x-10-6x^2-12x}{2x\left(x+2\right)}$
	↓	Subtrahiere im Zähler.
	$=$	$\displaystyle \frac{-5x-10}{2x\left(x+2\right)}$
	↓	Klammere $- 5$ im Zähler aus.
	$=$	$\displaystyle \frac{-5\left(x+2\right)}{2x\left(x+2\right)}$
	↓	Kürze $(x+2)$ .
	$=$	$\displaystyle -\frac{5}{2x}$

$\displaystyle \frac{74x-34}{x+1}\cdot\frac{x^2+1}{74x+34}$	$=$	$\displaystyle \frac{\left(74x-34\right)\left(x^2+1\right)}{\left(x+1\right)\left(74x+34\right)}$
	↓	Klammere die $2$ aus.
	$=$	$\displaystyle \frac{2\left(37x-17\right)\left(x^2+1\right)}{\left(x+1\right)\cdot2\left(37x+17\right)}$
	↓	Kürze die $2$ .
	$=$	$\displaystyle \frac{\left(37x-17\right)\left(x^2+1\right)}{\left(x+1\right)\left(37x+17\right)}$

$\displaystyle \frac{az}{z-a}:\frac{a^2z^3}{az-a^2}$	$=$	$\displaystyle \frac{az}{z-a}:\frac{a^2z^3}{a(z-a)}$
	↓	Division durch einen Bruch $\rightarrow$ Multiplikation mit dem Kehrwert.
	$=$	$\displaystyle \frac{az\cdot a\left(z-a\right)}{\left(z-a\right)\cdot a^2z^3}$
	↓	Fasse die Faktoren mit Potenzschreibweise zusammen.
	$=$	$\displaystyle \frac{a^2\cdot z\left(z-a\right)}{\left(z-a\right)\cdot a^2z^3}$
	↓	Kürze $a^2z\;(z-a)$ .
	$=$	$\displaystyle \frac{1}{z^2}$

$\displaystyle \dfrac{\;\;\displaystyle\frac JC\;\;}J$	$=$	$\displaystyle \frac JC:J$
	$=$	$\displaystyle \frac JC\cdot\frac1J$
	$=$	$\displaystyle \frac J{C\cdot J}$
	$=$	$\displaystyle \frac 1C$

$\displaystyle \dfrac J{\;\displaystyle\frac JC\;}$	$=$	$\displaystyle J\;:\frac JC$
	$=$	$\displaystyle J\cdot\frac CJ$
	$=$	$\displaystyle \frac{J\cdot C}J$
	$=$	$\displaystyle \frac C1$
	$=$	$\displaystyle C$

$\displaystyle \dfrac{\;{\displaystyle\frac1{x^2}}-2\;}{1-\displaystyle\frac1x}$	$=$	$\displaystyle \frac{\;\displaystyle\frac{1-2x^2}{x^2}\;}{\displaystyle\frac{x-1}x}$
	↓	Dividiere.
	$=$	$\displaystyle \frac{1-2x^2}{x^2}\cdot\frac x{x-1}$
	$=$	$\displaystyle \frac{\left(1-2x^2\right)x}{x^2\left(x-1\right)}$
	↓	Kürze durch x.
	$=$	$\displaystyle \frac{1-2x^2}{x\left(x-1\right)}$

$\displaystyle 36x^2-16x$	$=$	$\displaystyle 0$
	↓	Klammere $4x$ aus.
$\displaystyle 4x\cdot(9x-4)$	$=$	$\displaystyle 0$