Die molare Masse gibt an, wie viel ein Mol eines Stoffes wiegt.
Ein Mol ist immer dieselbe Anzahl an Teilchen, aber ein Mol von verschiedenen Stoffen unterscheidet sich stark im Gewicht, da unterschiedliche Teilchen unterschiedlich schwer sind.

Molare Masse eines Atoms
Die molare Masse eines Atoms kannst du in deinem Periodensystem ablesen. Hier steht sie rechts neben dem Elementsymbol.
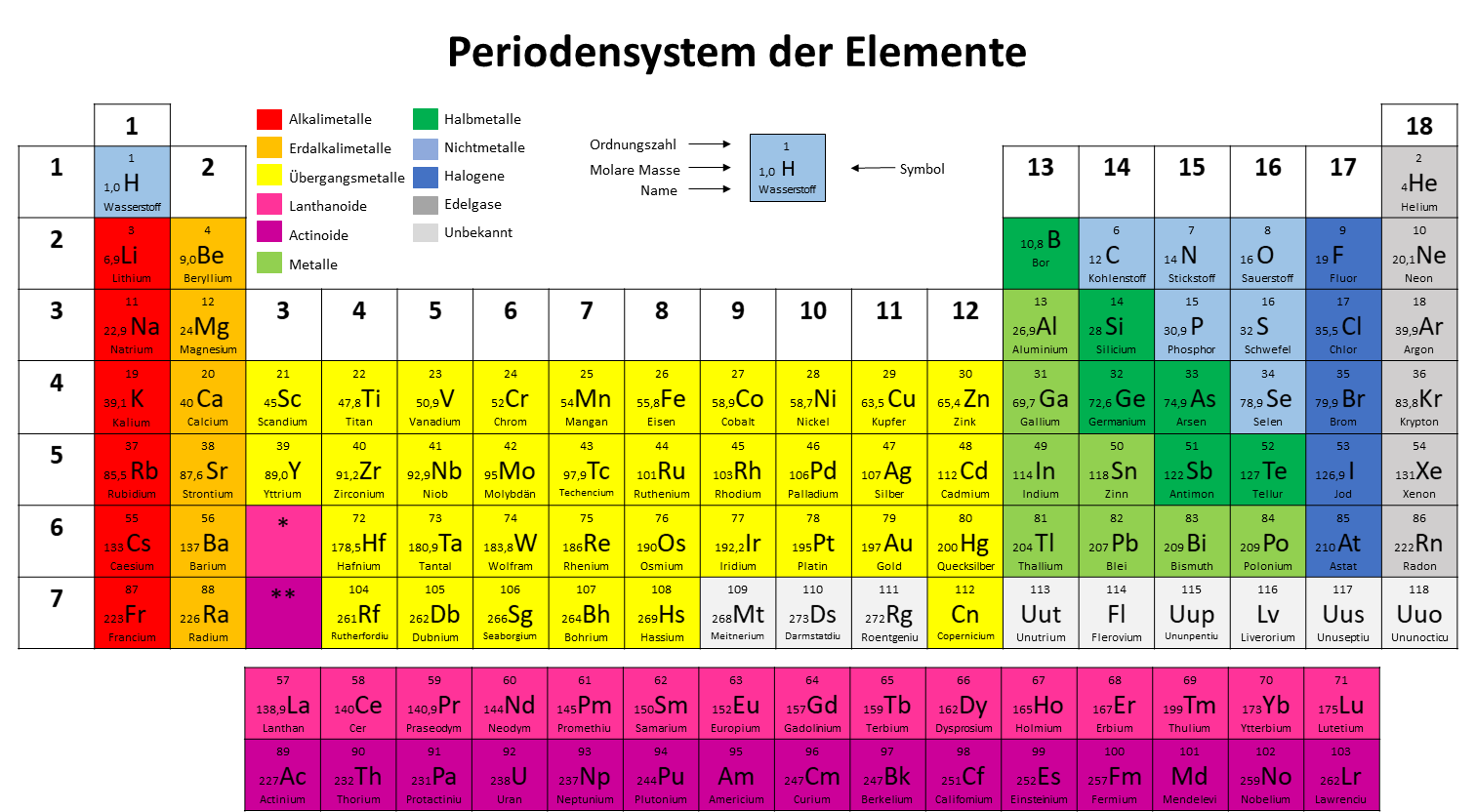
Die Molare Masse von Gold () ist beispielsweise .

Molare Masse eines Moleküls
Im Periodensystem kannst du also die molare Masse einzelner Atome ablesen. Im Folgenden kannst du nachlesen, wie du die Molare Masse von Stoffen berechnen kannst.
Die molare Masse eines Moleküls setzt sich zusammen aus den molaren Massen der einzelnen Atome. Die molaren Massen der einzelnen Atome des Moleküls werden addiert, um die molare Masse eines Moleküls zu erhalten.
Beispiel (Wasser)
Um die molare Masse von Wasser berechnen zu können, brauchst du zunächst die Summenformel von Wasser:
Wasser besteht also aus zwei Wasserstoffatomen () und einem Sauerstoffatom ().
Die molare Masse von Wasserstoff ist:
Die molare Masse von Sauerstoff ist:
Die molare Masse von Wasser setzt sich aus diesen molaren Massen zusammen:

Bei Salzen und Metallen müssen wir die Verhältnisformel betrachten und die molaren Massen der Atome in diesem Verhältnis addieren.
Beispiel (Kochsalz)
Um die molare Masse von Kochsalz berechnen zu können, brauchst du zunächst die Verhältnisformel von Kochsalz:
Die kleinste Einheit von Kochsalz besteht also aus einem Natriumatom () und einem Chloratom ().
Die molare Masse von Natrium ist:
Die molare Masse von Chlor ist:

Die molare Masse von Kochsalz setzt sich aus diesen molaren Massen zusammen:
