Ähnlichkeit von Dreiecken

Dreiecke werden als ähnlich bezeichnet, wenn sie sich in ihrer Form exakt gleichen. Dies ist dann der Fall, wenn ein Dreieck durch ein anderes hervorgeht durch:

Verschiebung
Drehung
Spiegelung
Vergrößerung/Verkleinerung (Streckung)

Bei Dreiecken gibt es zusätzlich einige Methoden, Ähnlichkeit zu überprüfen, die sogenannten Ähnlichkeitssätze:

SSS-Satz
WW-Satz
SWS-Satz
SsW-Satz

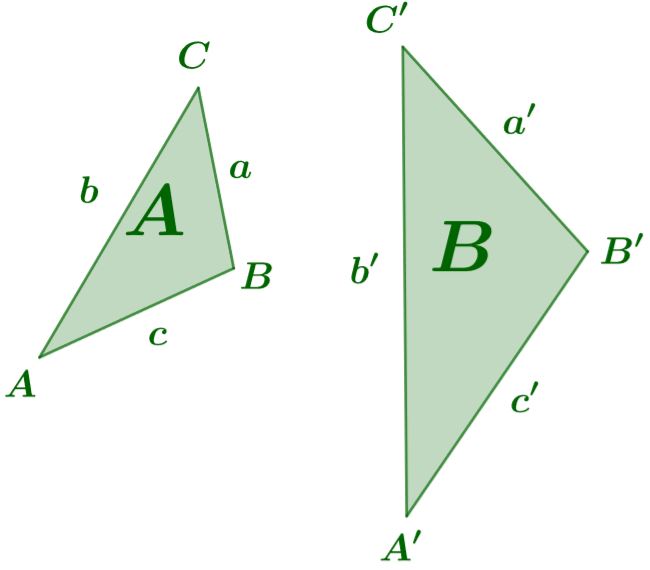
Ähnlichkeitssätze des Dreiecks

Zwei Dreiecke können auf Ähnlichkeit überprüft werden, wenn genügend Informationen über ihre Seiten bzw. Winkel bekannt ist. Hierzu müssen nicht alle Seiten und Winkel gegeben sein, sondern nur eine kleine Auswahl.

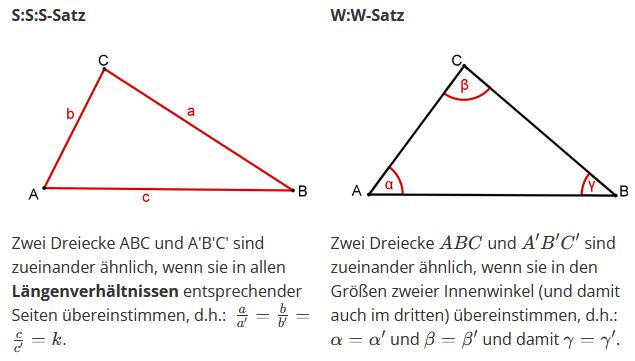
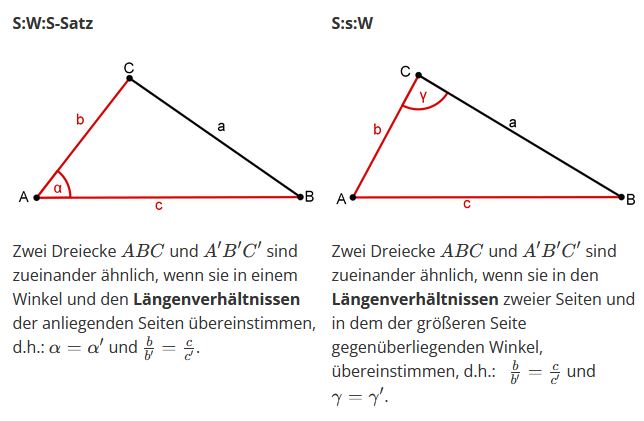
Beispiele zu den Ähnlichkeitssätzen

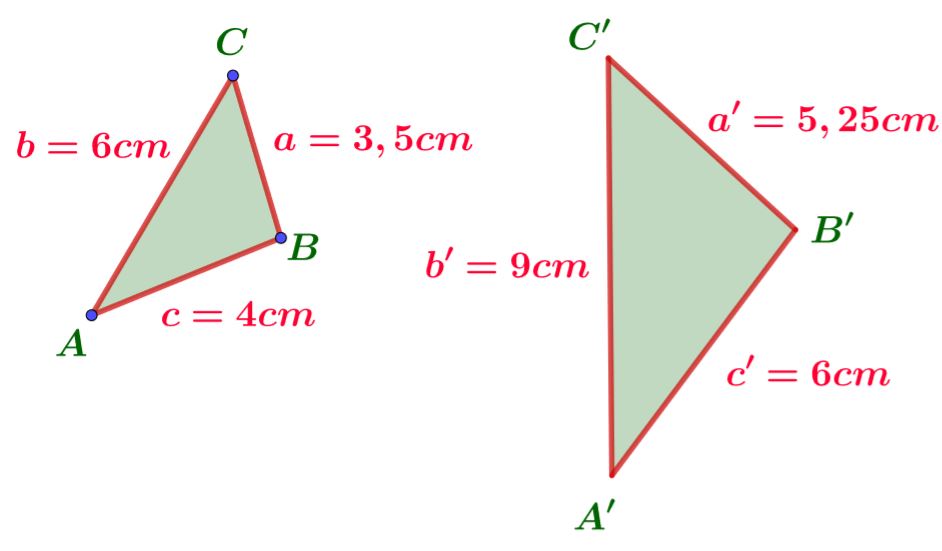
SSS-Satz

Gegeben sind alle Seitenlängen der beiden Dreiecke. Sie sind ähnlich, sobald alle Seitenverhältnisse gleich sind. Es gilt:

$\frac{a'}{a}=\frac{5{,}25}{3{,}5}=1{,}5$
$\frac{b'}{b}=\frac{9}{6}=1{,}5$
$\frac{c'}{c}=\frac{6}{4}=1{,}5$

Die Seitenverhältnisse sind gleich, damit sind die Dreiecke ähnlich und besitzen den Ähnlichkeitsfaktor $k=1{,}5$ .

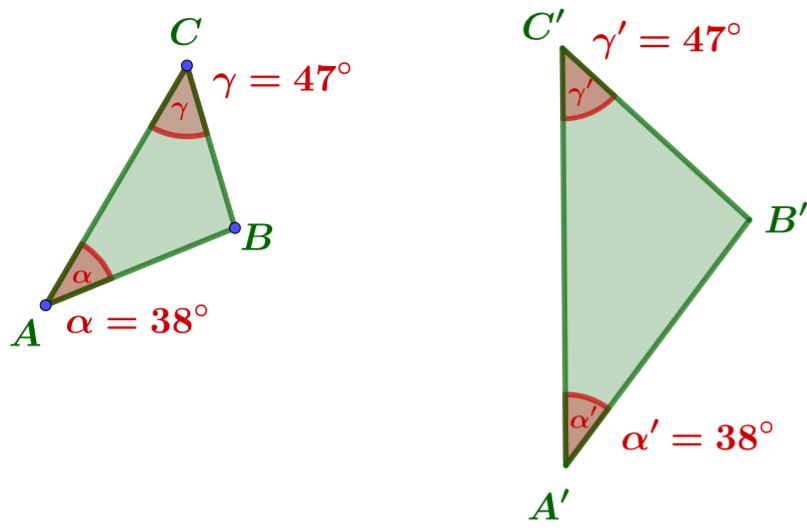
WW-Satz

Stimmen zwei Dreiecke in zwei ihrer Winkel überein, sind sie ähnlich.

$\alpha=\alpha'=38°$
$\gamma=\gamma'=47°$

Da diese Winkel übereinstimmen, sind die Dreiecke ähnlich. Aufgrund der Winkelsumme stimmen auch $\beta$ und $\beta'$ überein.

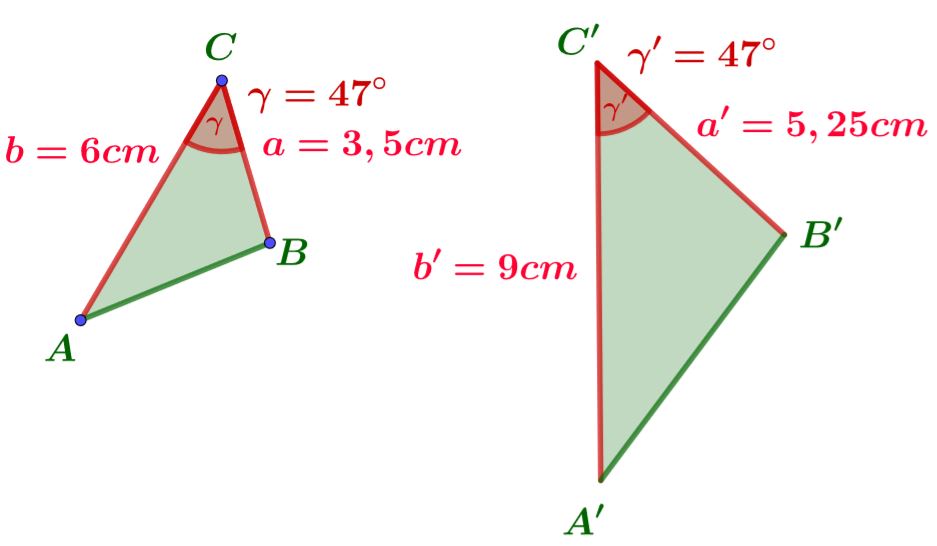
SWS-Satz

Wir überprüfen zwei Seitenverhältnisse und den Winkel, der zwischen den gegebenen Seiten liegt.

$\frac{\beta'}{\beta}=\frac{9}{6}=1{,}5$
$\frac{a'}{a}=\frac{5{,}25}{3{,}5}=1{,}5$
$\gamma=\gamma'=47°$

$\Rightarrow$ Die Dreiecke sind ähnlich.

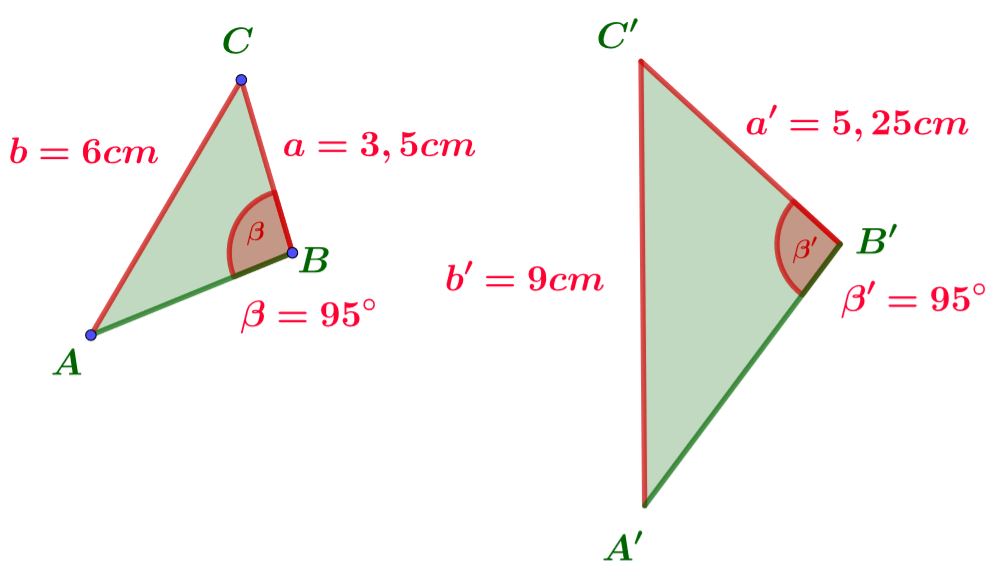
SsW-Satz

Wir überprüfen wieder zwei Seitenverhältnisse und den Winkel, der gegenüber von der längeren Seite liegt.

$\frac{\beta'}{\beta}=\frac{9}{6}=1{,}5$
$\frac{a'}{a}=\frac{5{,}25}{3{,}5}=1{,}5$
$\beta=\beta′=95°$

Übungsaufgaben: Ähnlichkeit von Dreiecken

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kongruenz und Ähnlichkeit von Dreiecken

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?