1 Einführung
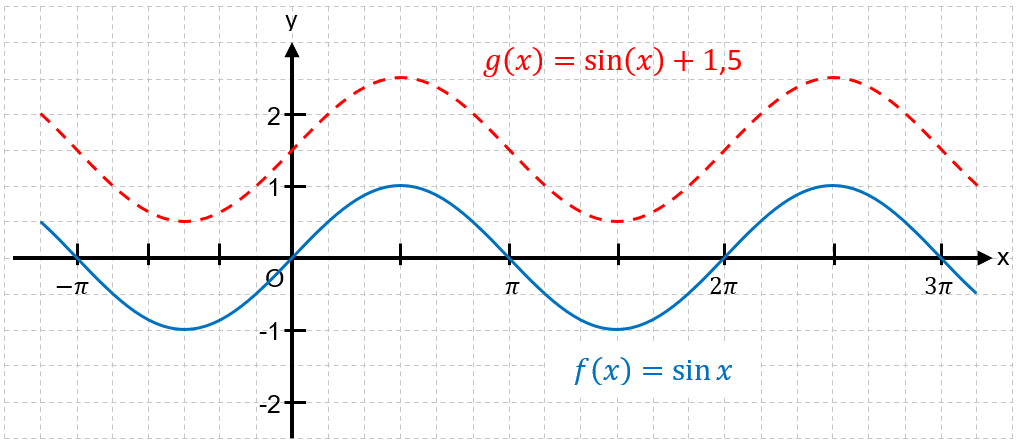
Verändert man den Funktionsterm der Sinusfunktion mithilfe von Parametern, z. Bsp. oder , so gehen die zugehörigen Graphen aus dem der Sinusfunktion durch Strecken, Verschieben oder Spiegeln hervor.
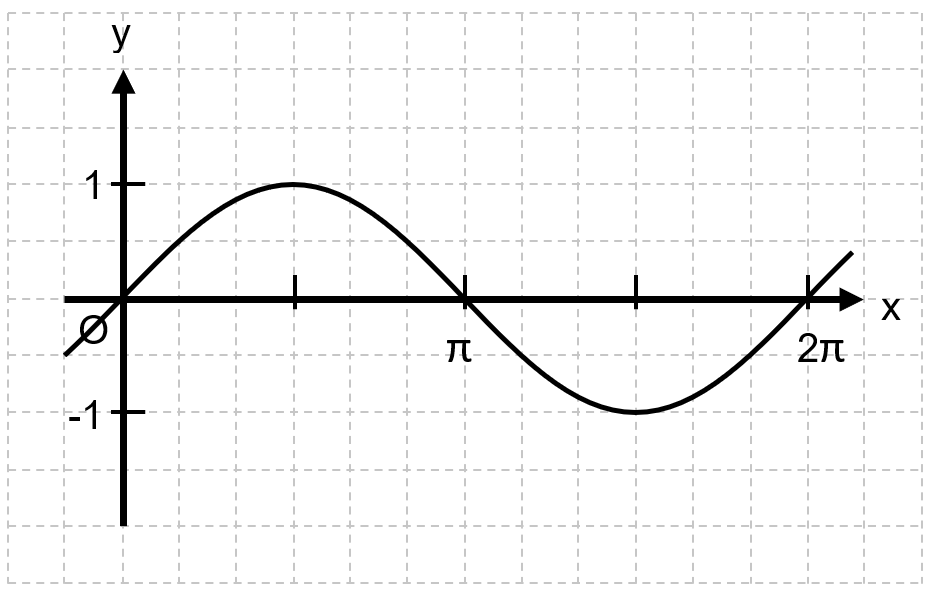
In diesem Kurs wird der Einfluss der Paramater und bei der allgemeinen Sinusfunktion untersucht.
Auf der nächsten Seite wird der Einfluss des Parameters bei der Funktion untersucht.
2 Parameter a
Untersuche die Auswirkung des Parameters a auf den Graphen der Funktion, indem du durch Betätigung des Schiebereglers oberhalb der Sinuskurve den Parameter a veränderst.
Beantworte anschließend die Fragen unterhalb des Geogebra-Applets.
Laden
mit und
Streckung mit dem Faktor || in y-Richtung
Für wird der Graph der Sinusfunktion an der x-Achse gespiegelt.
Wertemenge: W = [-||; ||]
Laden
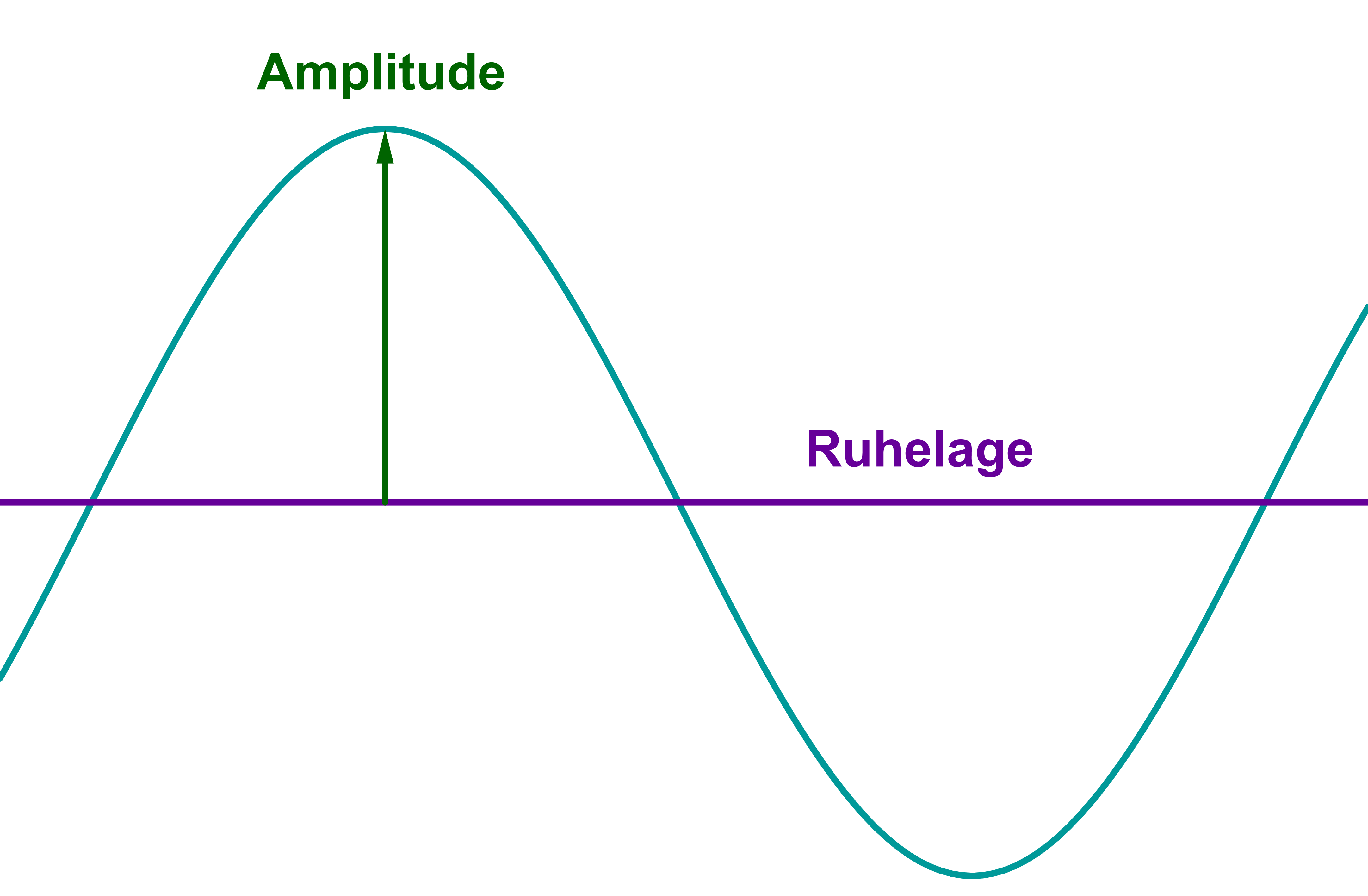
Der Betrag von a wird als Amplitude bezeichnet.
Auf der nächsten Seite wird der Einfluss des Parameters bei der Funktion untersucht.
3 Parameter b
Untersuche die Auswirkung des Parameters b auf den Graphen der Funktion, indem du durch Betätigung des Schiebereglers oberhalb der Sinuskurve den Parameter b veränderst.
Beantworte anschließend die Fragen unterhalb des Geogebra-Applets.
Laden
mit und b 0
Streckung um Faktor in x-Richtung
Falls wird der Graph der Sinusfunktion an der y-Achse gespiegelt.
Periode:
Nullstellen: mit k
Laden
Auf der nächsten Seite wird der Einfluss des Parameters bei der Funktion untersucht.
4 Parameter c
Untersuche die Auswirkung des Parameters c auf den Graphen der Funktion, indem du durch Betätigung des Schiebereglers oberhalb der Sinuskurve den Parameter c veränderst.
Beantworte anschließend die Fragen unterhalb des Geogebra-Applets.
Laden
mit
Verschiebung um in x-Richtung
Nullstellen mit
Laden
Auf der nächsten Seite wird der Einfluss des Parameters bei der Funktion untersucht.
5 Parameter d
Untersuche die Auswirkung des Parameters auf den Graphen der Funktion, indem du durch Betätigung des Schiebereglers oberhalb der Sinuskurve den Parameter veränderst.
Beantworte anschließend die Fragen unterhalb des Geogebra-Applets.
Laden
mit
Verschiebung um d in y-Richtung
Laden
Auf der nächsten Seite findest du eine Zusammenfassung der bisherigen Ergebnisse.
6 Zusammenfassung
Allgemeine Sinusfunktion
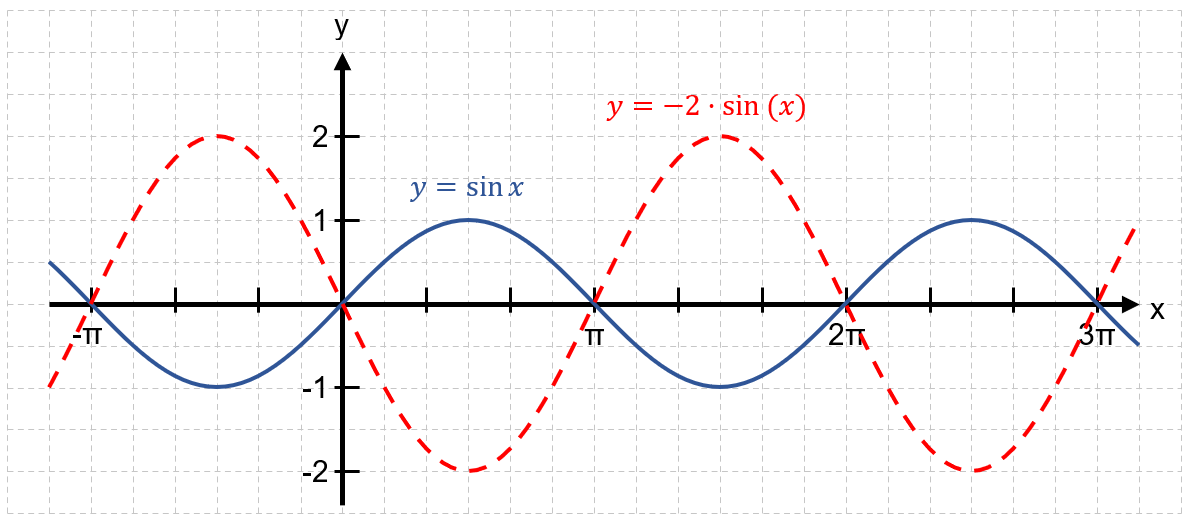
Streckung mit dem Faktor || in y-Richtung
Wertemenge: W = [-||; ||]
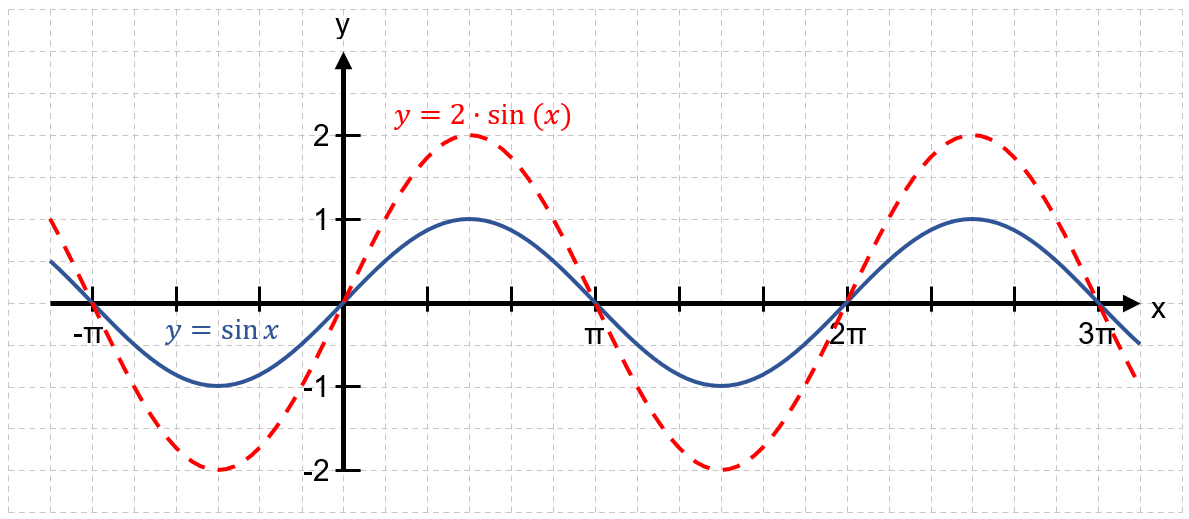
Für a<0 wird der Graph der Sinusfunktion an der x-Achse gespiegelt.
Streckung um Faktor in x-Richtung
Periode:
Wertemenge: W =[-1;1]
Nullstellen: mit k
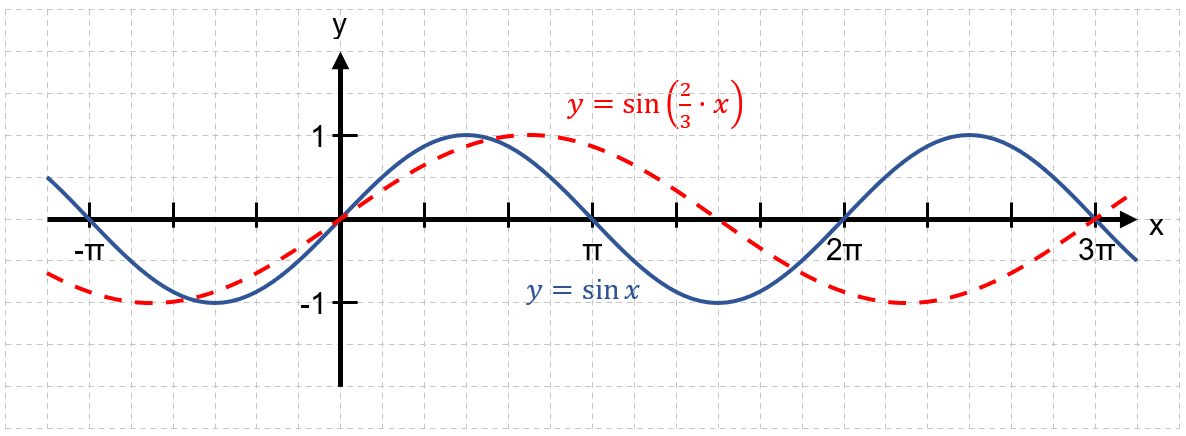
Falls wird der Graph der Sinusfunktion an der y-Achse gespiegelt.
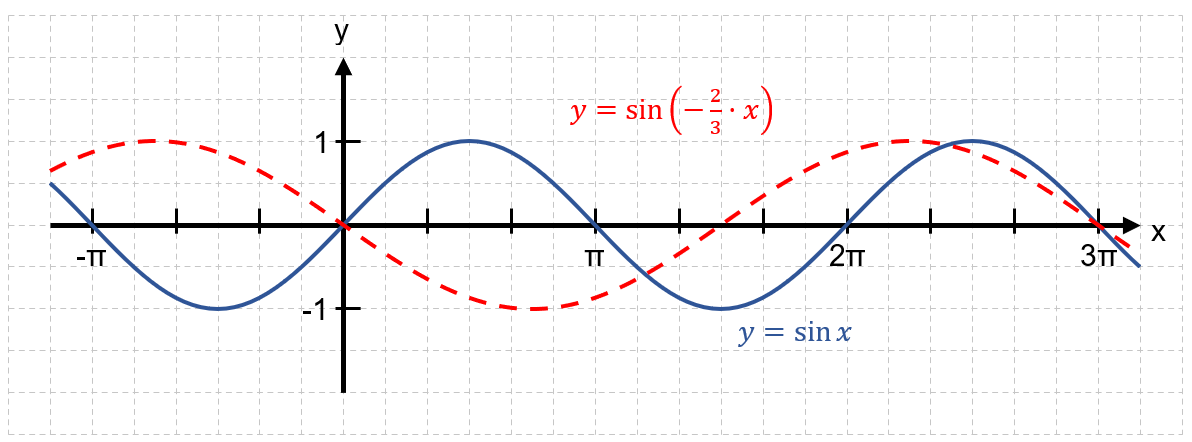
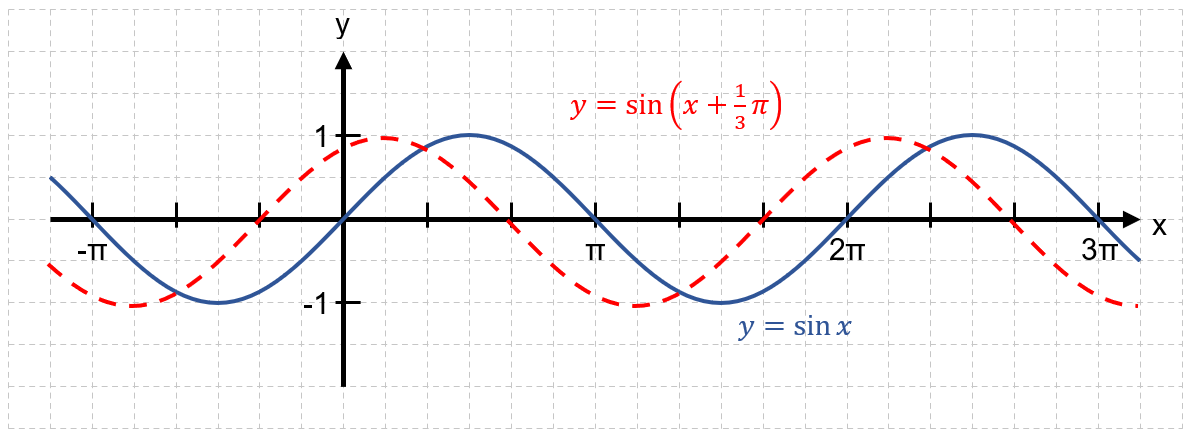
Verschiebung um in x-Richtung
Nullstellen mit
Verschiebung um d in y-Richtung
Auf der nächsten Seite lernst du, wie man zu einem gegebenen Graphen die zugehörige Funktionsgleichung bestimmen kann.
7 Bestimmen der Funktionsgleichung bei gegebenen Graphen
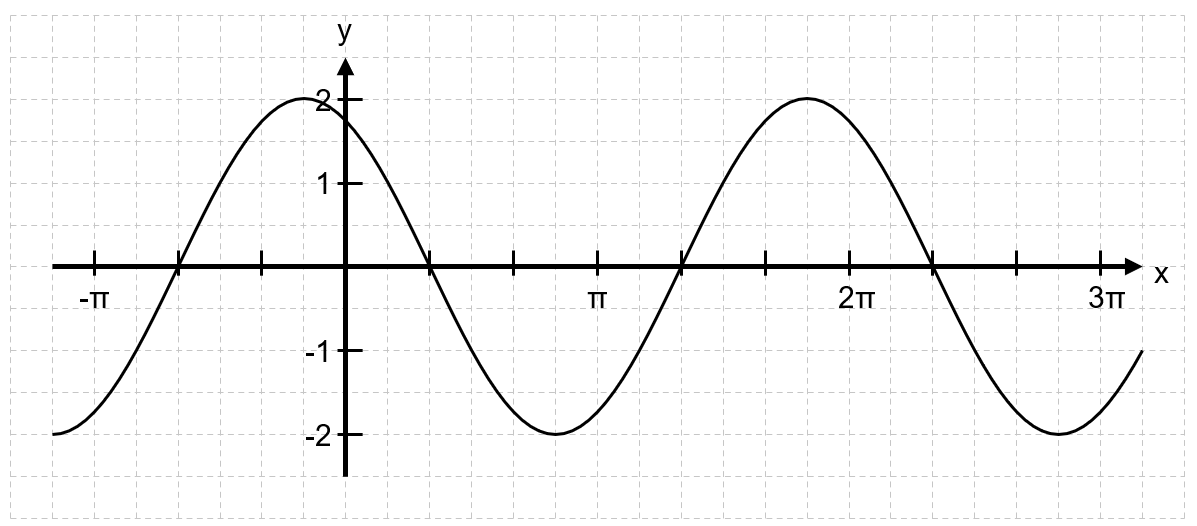
Ermittle zum folgenden Graphen der Funktion eine Funktionsgleichung.
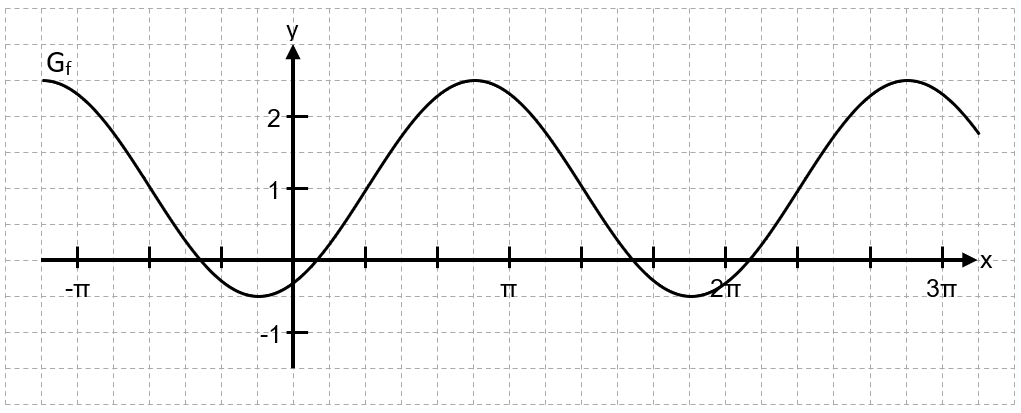
Schritt 1
Zeichne eine Parallele zur x-Achse ein, von der die Hoch- und Tiefpunkte des Graphen gleich weit entfernt sind. Diese Parallele nennt man Mittellinie.
Schritt 2
Suche einen Schnittpunkt S von und der Mittellinie, so dass in der Umgebung von S steigt und der in sich in der Nähe der y-Achse befindet (Nur nötig, damit Lösung eindeutig ist). Diesen Schnittpunkt nennt man auch Startpunkt S.
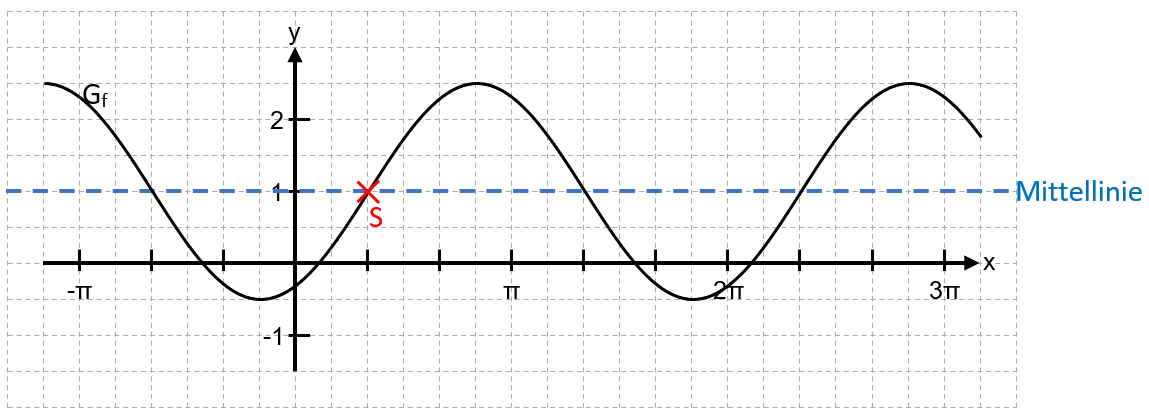
Schritt 3
Nun kann man die Parameter folgendermaßen bestimmen:
a: Der Abstand, den die Hoch- bzw. Tiefpunkte von der Mittellinie haben, ist a. Diesen Abstand nennt man Amplitude.
Vom Punkt S (oder von einem Hochpunkt oder von einem Tiefpunkt) ausgehend bestimmt man die Periode p und damit den Parameter b mit .
c: |c| ist der Abstand von S zur y-Achse. Dabei ist c positiv, wenn S links von der y-Achse liegt, und c ist negativ, wenn S rechts von der y-Achse liegt. Bemerkung: c ist nicht eindeutig bestimmbar, da es mehrere Möglichkeiten für den Startpunkt gibt.
d: Die Verschiebung von S in y-Richtung ist d.
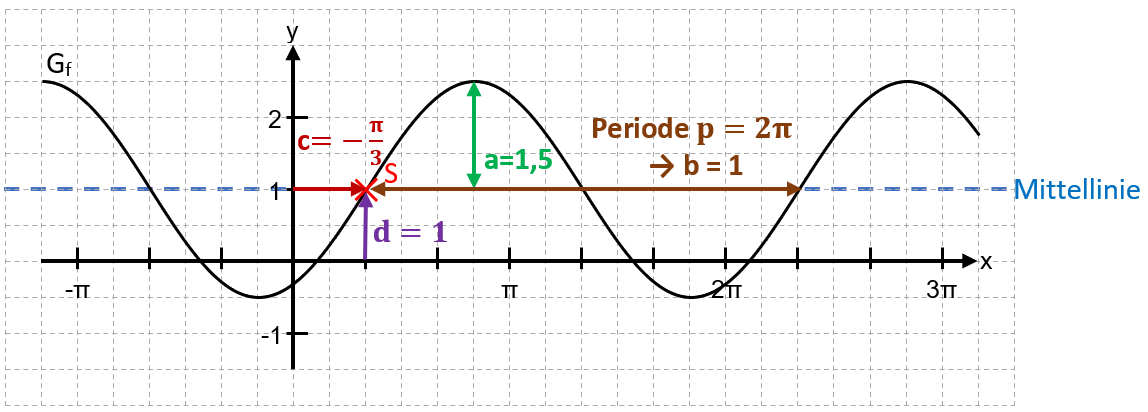
Schritt 4
Aufstellen der Funktionsgleichung
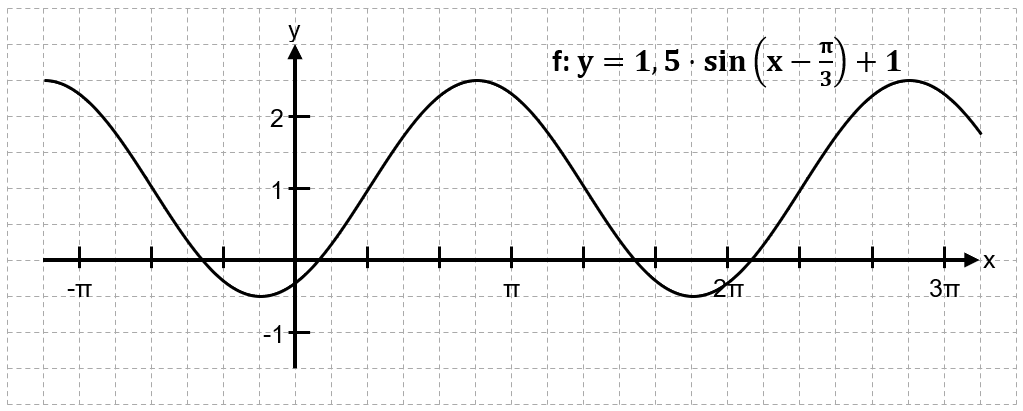
Aufgabe 1:
Bestimme eine Funktionsgleichung zum folgenden Graphen.
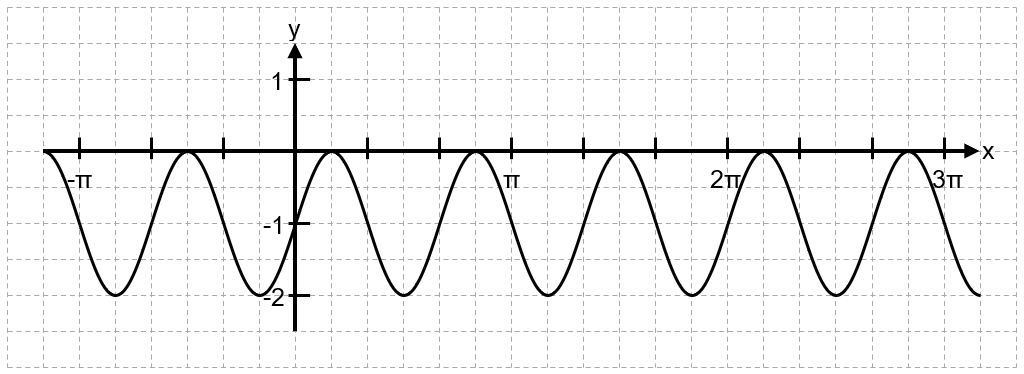
Aufgabe 2:
Bestimme eine Funktionsgleichung zum folgenden Graphen.