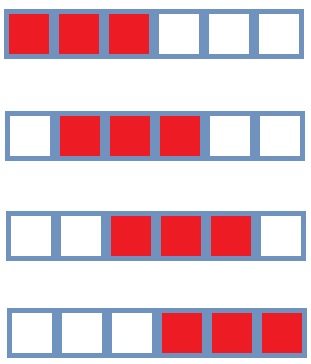
3 Jungen und 3 Mädchen setzen sich wahllos nebeneinander auf eine Bank. Wie hoch ist die Wahrscheinlichkeit dafür, dass
links außen ein Mädchen sitzt
die 3 Jungen nebeneinander sitzen
eine bunte Reihe entsteht?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?