Der Begriff Funktion ist vielen aus der Mathematik bekannt, diese sind dort mithilfe von mathematischen Formeln eindeutig festgelegt. Funktionen werden aber auch in der Informatik gebraucht, damit von einem Programm etwas berechnet werden kann.

Die Funktion als Blackbox

Eine Funktion kannst du im Wesentlichen mit einer Blackbox vergleichen, einer schwarzen Kiste, wo du am Anfang vielleicht erst einmal gar nicht weißt, was in dieser Kiste ist.

Eine Funktion ist im Grunde in der Informatik immer gleich aufgebaut. Als Erstes findet eine Eingabe statt, dann wird die Funktion selbst ausgeführt und als Letztes findet eine Ausgabe statt.

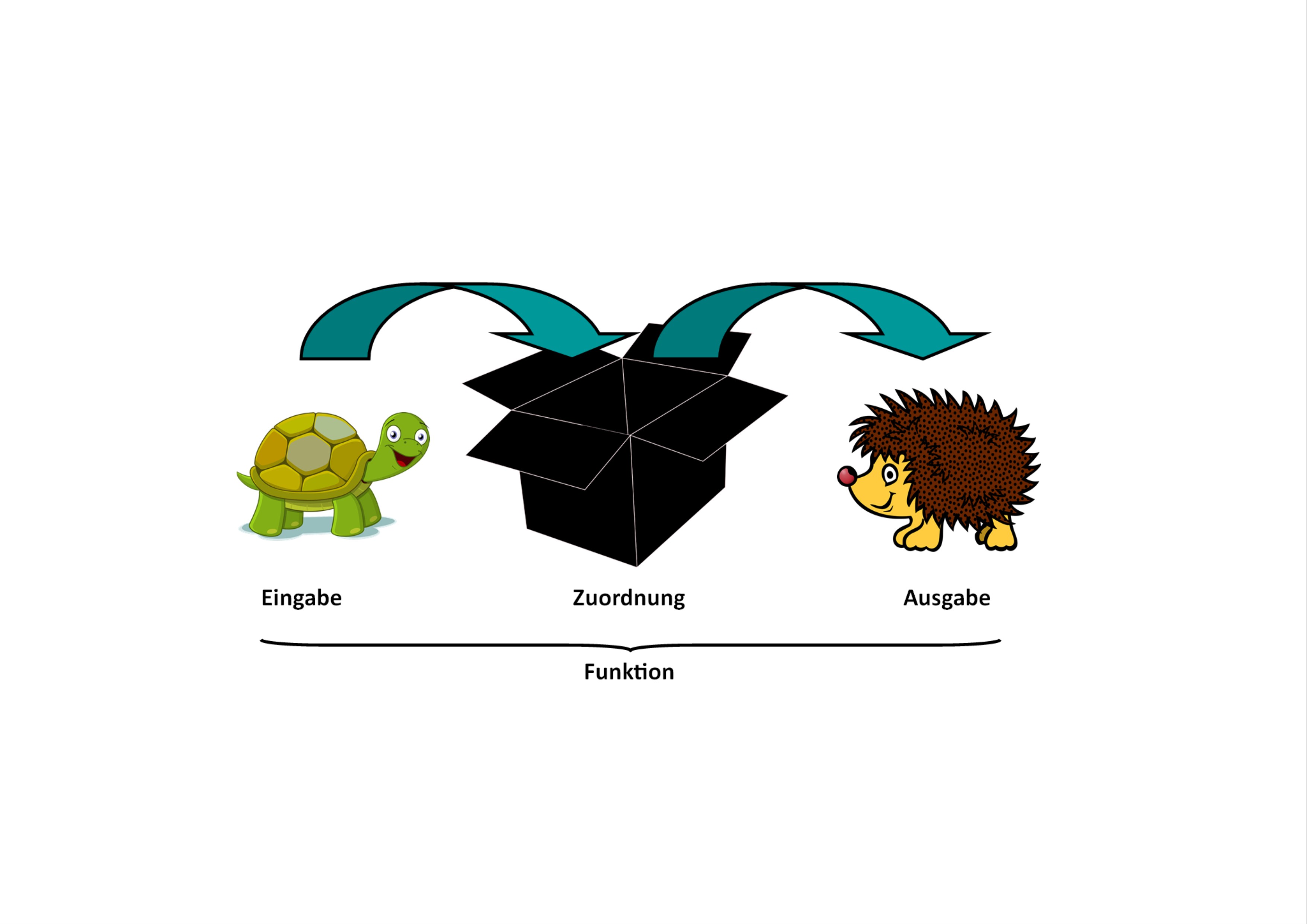
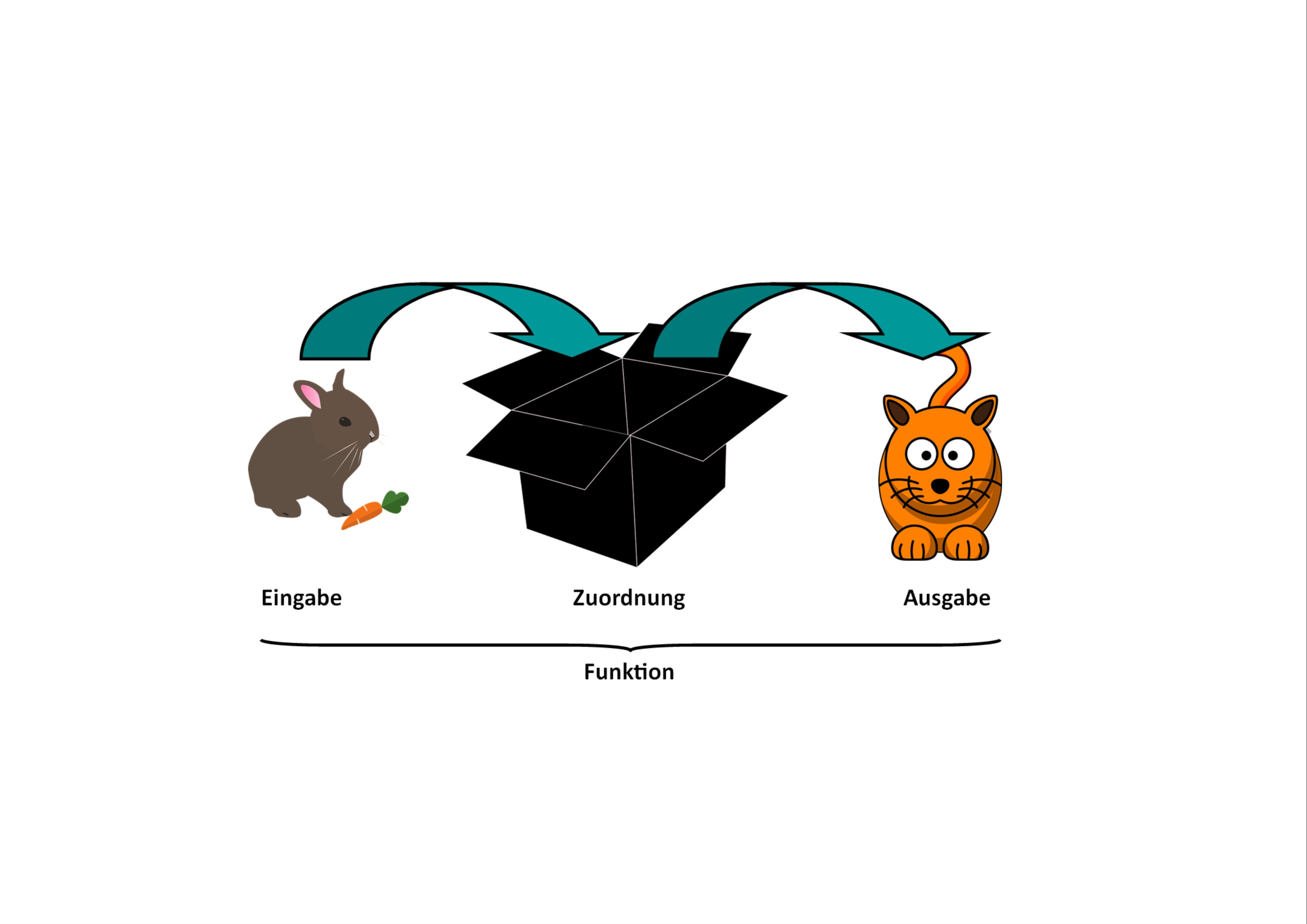
Allgemein gesagt, beschreibt eine Funktion einen eindeutigen Vorgang. Für die Eingabe benötigt man Eingabewerte, welche verarbeitet werden. Die Verarbeitung heißt in der Informatik Zuordnung. Aus den Eingabewerten und der Zuordnungsvorschrift folgt eine Ausgabe, der Ausgabewert.

Wichtig ist, dass es sich um eine eindeutige Zuordnung handeln muss, das heißt, es muss bei gleichen Eingabewerte, den gleichen Ausgabewert erzeugen.

Beispiel:

Du legst einen Hasen in die Kiste und es kommt eine Katze heraus. Du legst wieder einen Hasen in die Kiste, doch diesmal kommt ein Hund heraus.

$\Rightarrow \backslash Rightarrow$ keine Funktion, da die Zuordnungsvorschrift zwei verschiedene Ausgabewerte erzeugt.

Funktionen können einen oder mehrere Eingabewerte besitzen. So ist zum Beispiel die Funktion SUMME() für die Zahlen $\mathrm{1,2}1\{,\}2$ und $33$ wie folgt aufgebaut:

SUMME(1;2;3)

Möchtest du die Funktion allgemein beschreiben, kannst du die Zahlen durch Platzhalter ersetzen, sogenannte Eingabeparameter. Jeder einzelne Eingabeparameter besitzt einen Eingabewert.

Beispiel der Funktion SUMME() allgemein:

SUMME(a; b; ...)

Wird die Funktion Summe nun ausgeführt, werden die einzelnen Eingabewerte ausgewertet und addiert.

Vordefinierte Funktionen

In jedem Tabellenkalkulationsprogramm gibt es eine Vielzahl an vordefinierten Funktionen. Diese haben den Sinn, dass wichtige und häufige Probleme bereits gelöst wurden und deshalb als Funktion zur Verfügung steht.

Ein einfaches Beispiel ist hierfür die Funktion HEUTE(). Diese gibt immer das aktuelle Datum aus, damit der Ersteller einer Tabelle es nicht jedes Mal selbst machen muss.

Außerdem gibt es zahlreiche Funktionen, welche mathematische oder andere Probleme lösen. So gibt es zum Beispiel die Funktion MITTELWERT(), welche für mehrere Zahlen den Mittelwert von diesen ermittelt. Der Ersteller der Tabelle muss also nicht die mathematische Formel hierfür kennen, die Berechnung erledigt die vordefinierte Funktion selbst.

Funktionsanfang

Um einem Tabellenkalkulationsprogramm zu zeigen, dass gleich eine Funktion beginnt, muss diese bestimmt gekennzeichnet werden. Dies geschieht immer mit einem = vor der eigentlichen Funktion. Das = verrät deinem Programm, dass nun eine Funktion beginnt.

Beispiel

Du möchtest $3+43+4$ ausrechnen.

Wähle die Zelle aus, in welcher die Berechnung stattfinden soll und tippe dort ein: =3+4

Mit der Bestätigung durch die Enter Taste, wird dir das richtige Ergebnis $77$ angezeigt.

Die meisten Funktionen, die du in deinem Tabellenkalkulationsprogramm verwenden wirst, sind Funktionen mit mehreren Eingabeparametern. Diese sind dabei wie bereits vorher gelernt wie folgt allgemein aufgebaut:

Funktionsname(a;b;...)

Folgende Eigenschaften, sind nun bei mehrstelligen Funktionen besonders zu beachten.

Reihenfolge der Parameter

Oft ist es bei Funktionen wichtig, in welcher Reihenfolge die Eingabeparameter stehen. Schau dir dafür ein Beispiel mit der Funktion MINUS() an:

=MINUS(7;5), ist gleichbedeutend mit $=7-5=7-5$ und liefert den Ausgabewert $22$.

=MINUS(5;7), ist hingegen gleichbedeutend mit $=5-7=5-7$ und liefert den Ausgabewert $-2-2$.

In der Mathematik nennt man dies übrigens nicht kommutativ. Wäre die Funktion kommutativ, dürfte man die beiden Eingangsparameter vertauschen, wie zum Beispiel bei der Funktion SUMME().

Trennung der Parameter

Bei jeder mehrstelligen Funktion werden die Parameter durch den Semikolon (;) getrennt.

Das bedeutet, immer du noch ein Eingangsparameter hinzufügen willst, setzt du hinter das vorherige ein ;.

Beispiel:

Es soll folgende Summe ausgerechnet werden: $1+12+4+7+81+12+4+7+8$

Lösung: SUMME(1;12;4;7;8)

Vorsicht: Bei einigen Funktionen lassen sich nicht beliebig viele Eingangsparameter hinzufügen. Bei der Funktion RUNDEN() ergibt es zum Beispiel keinen Sinn, dort $55$ Eingangsparameter zu haben. Die Funktion weiß dann nicht mehr, was sie tun soll.

Lies den Artikel Datenflussdiagramm. Mache im Anschluss mit dem Kurs hier weiter.

Bisher hast du für Funktionen gelernt, dass diese ein oder mehrere Eingangsparameter haben können. Die Eingangsparameter waren bisher jedoch in den Beispielen immer nur ein Platzhalter für Zahlenwerte.

Oft benötigt man jedoch nicht nur einen bestimmten Zahlenwert, sondern möchte diesen auch ändern können und dann gleich den neuen Ausgabewert sehen. Hierfür verwendest du das Konzept der Variablen.

Eine Variable ist nichts anderes als ein Platzhalter für Werte, in Tabellenkalkulationsprogrammen bedeutet das, dass du einer bestimmten Zelle einen bestimmten Wert zuordnen kannst.

Beispiel:

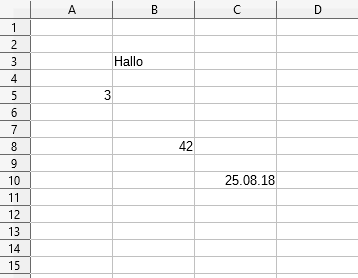
Funktionen können nun mit diesen Variablen ihre Berechnungen ausführen. Möchtest du zum Beispiel die Zahlen $33$ und $44$ aus unserem Beispiel addieren, sind bei deiner Funktion die Eingangsparameter die Zellen A5 und B8.

Funktion: SUMME(A5;B8)

Funktionen können viele Eingangsparameter besitzen. Diese können durch Variablen, wie du auf der vorherigen Kursseite gelernt hast, repräsentiert werden.

Oft ist es notwendig, mit dieser großen Anzahl an Eingabewerten Funktionen auszuführen. Stehen diese Werte in deiner Tabelle in zusammenhängenden Blöcken, gibt es eine einfachere Methode als alle einzeln einzutippen, der sogenannte Bereichsoperator.

Funktionsweise des Bereichsoperators

Möchtest du den Bereichsoperator verwenden, benötigst du immer die Zelle der linken oberen Ecke und die Zelle der rechten unteren Ecke. Möchtest du nur eine Spalte in einem Bereichsoperator zusammenfassen, nimmst du die oberste und unterste Zelle, bei einer Zeile nimmst du die am linkesten und rechtesten Zellen. Die Zellen werden durch einen : verbunden, wie zum Beispiel: A1:B4 bedeutet der Bereich von der Zelle A1 bis zur Zelle B4.

Beispiel

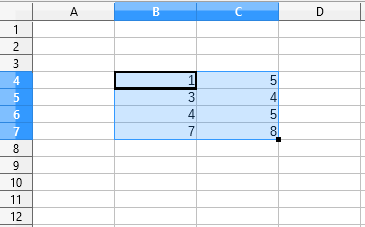
Möchtest du nun zum Beispiel die Summe für diesen Bereich berechnen, ist dein Eingabewert dein Bereichsoperator.

Beispiel:

Für den oben genannten Bereich der Zellen B4 bis C8 kann die Summe wie folgt berechnet werden: SUMME(B4:C8)

Viele Probleme lassen sich in der Regel nicht von einer einzigen Funktion lösen, so brauchst du zum Beispiel zum Lösen der einfachen Rechnung $1\cdot 2+3\cdot 41\backslash cdot2+3\backslash cdot4$ die Funktionen SUMME() und PRODUKT().

Benötigst du mehrere Funktionen in einer Berechnung, nennt man diese Verkettung von Funktionen.

Was bedeutet das im Konkreten?

Verkettete Funktionen werden zuerst einzeln ausgeführt. Bleiben wir bei dem Beispiel von oben:

$1\cdot 2+3\cdot 41\backslash cdot2+3\backslash cdot4$

Zuerst rechnest du die Produkte $1\cdot 21\backslash cdot2$ aus und $3\cdot 43\backslash cdot4$ aus (Punkt vor Strich Regel). Im Anschluss berechnest du die Summe aus beiden Produkten.

In der Informatik bedeutet dies konkret an diesem Beispiel folgende Ausführung der Funktionen:

Die Ausgabewerte der Funktionen PRODUKT() werden also der Funktion SUMME() als Eingabewerte übergeben. Diese Übergabe der Argumente nennst du Verkettung von Funktionen.

Beachte:

Verkettete Funktionen werden immer von innen nach außen ausgeführt, das bedeutet, die inneren Funktionen liefern der äußersten Funktion deren Eingabewerte.