Das Rechnen ist eine Fähigkeit, in der uns Computer weit überlegen ist. Computer sind darin super schnell und präzise und machen eigentlich keine Fehler.
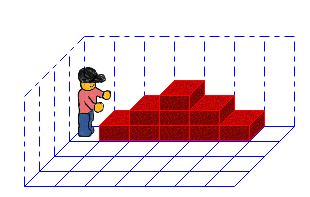
Die Treppen und Burgen von Robot Karol sind ja schön anzuschauen - aber um sich als praktische Sprache zu beweisen muss Karol zeigen, dass sie auch mit Zahlen umgehen kann.
Du: Aber Robot Karol besitzt gar keine Methoden zum Rechnen!?
InformatikerIn: hold my beer
3 hours later
It's done!
Eine InformatikerIn braucht keine vorgefertigten Methoden, wenn sie sich diese auch selber bauen kann. Dieser Artikel zeigt eine Möglichkeit, wie es geht. Ich versuche die einzelnen Schritte möglichst anschaulich darzustellen und zu erklären. Du kannst das Programm selbst mitprogrammieren.
Informationen darstellen
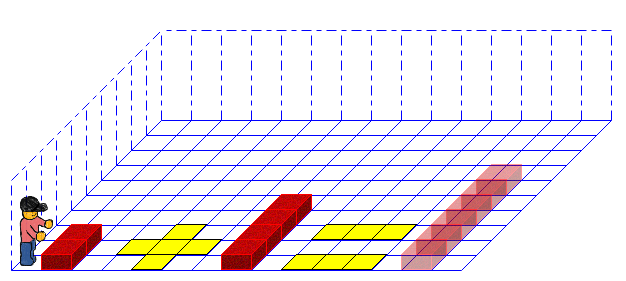
Wir verwenden eine sehr einfache Form der Zahlendarstellung: Die Zahl wird durch die Anzahl der Ziegel bestimmt, die übereinander liegen. Damit kann Karol gut arbeiten und ist auch schön anschaulich. Wir beschränken uns für das Erste auf den Zahlenbereich von 1 bis 9.
Rechenzeichen werden mit Marken gelegt. Im Bild oben sieht man die Rechnung . Hier sind jeweils noch die anderen Rechenarten dargestellt:
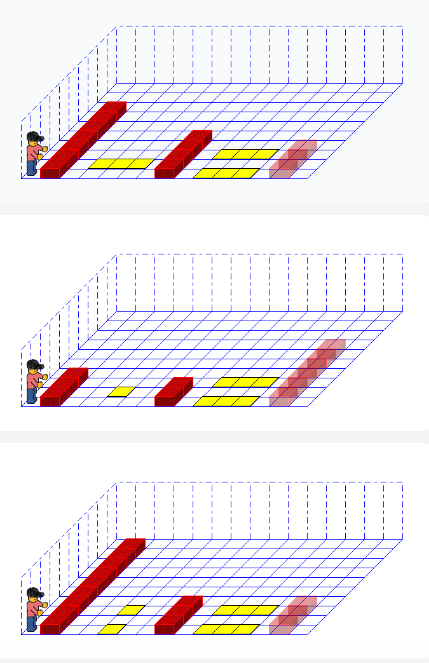
Ich habe mir diese Darstellung ausgesucht, weil sie schön anzuschauen ist. Ist hat man natürlich die Freiheit, andere Darstellungen zu verwenden. Diese Freiheit ist auch das Schöne am Programmieren.
Rechenart auslesen
Jetzt geht es ans Programmieren! Ich werde den didaktisch-wertvollen Weg gehen und nur mit Blöcken arbeiten. Das ist manchmal etwas leidvoll, aber irgendwie macht mir das auch Spaß - weird. Anyways. Nur mit Blöcken zu arbeiten heißt auch, dass ich wirklich nur Bausteine verwende, die schon bekannt sind. Keine geheimen Tricks. Alles transparent.
Let's go. Zuerst muss Karol erkennen, um welche Rechenart es sich handelt. Für jede Rechenart gibt es ein anderes Verfahren.
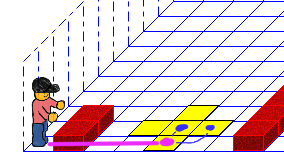
Ich teste zuerst das untere Feld. Wenn dort eine Marke liegt, dann kann es nur die Addition oder die Division sein. Um diese zu unterscheiden, gehe ich ein Feld rüber.
Falls auf dem Feld keine Marke liegt, dann sind es die beiden anderen Rechenarten. Um diese zu unterscheiden gehe ich ein Feld diagonal nach oben rechts. Mit bedingten Anweisungen sieht es so aus:
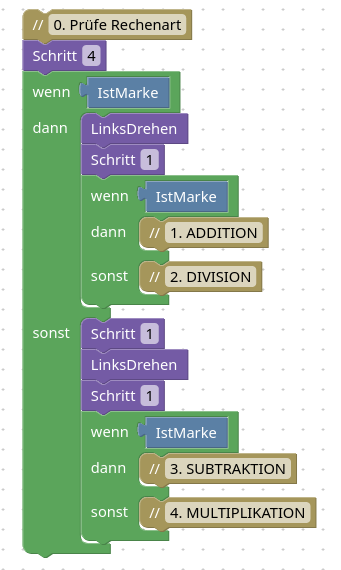
Hier haben wir also schön die 4 Rechenarten aufgetrennt und können uns einem nach dem anderen widmen.
1. Addition
Erstmal der grobe Plan: Ich gehe jeden der beiden Summanden durch und lege für den Ziegel ein Ziegel im Ergebnis. Es wird also zwei Programmteile geben, die recht ähnlich sind. Allerdings muss ich beachten, dass ich die Ziegel mit abbauen. Das macht und leider ein wenig mehr Arbeit.
1.1. Gehe zu Start
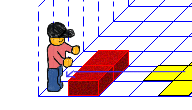
Karol muss erstmal wieder zur Startposition Das geht mit folgenden 5 Befehlen:
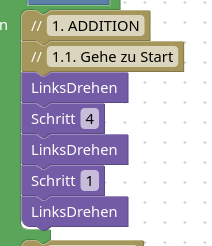
Schreibe alle folgenden Unterabschnitte nacheinander - sie sollen nicht verschachtelt sein.
1.2. Markiere Stapel
Wir wollen den Stapel nicht abbauen, deshalb brauchen wir eine andere Möglichkeit, die Position im Stapel zu speichern. Ich nutze dafür eine Marke. Die Anzahl der leeren Felder bis zur Wand entspricht dem aktuellen Wert:
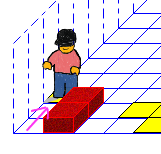
Karol soll also an den Ziegeln entlang gehen, die Marke setze und sich Richtung Wand drehen:
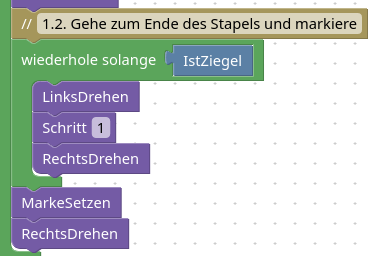
1.3. Anzahl Ziegel im Ergebnis legen

Jetzt wird Karol ihre Runden drehen. Dabei wird sie in 1.3.0 am Anfang des Ergebnis stapels stehen, in 1.3.1 zum Ende des Stapels laufen, in 1.3.2 den Ziegel setzen, in 1.3.3. zurücklaufen und schließelich in 1.3.4 die Marke um eins verschicken.
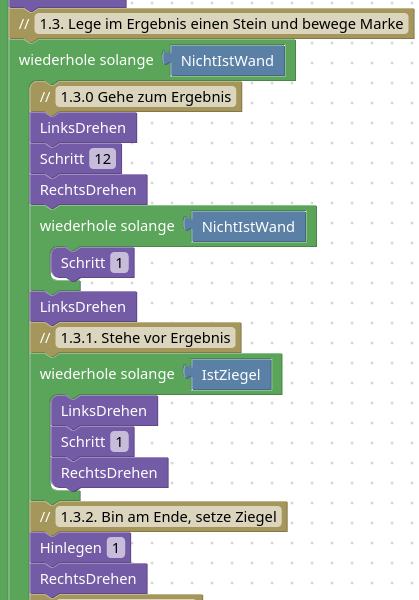

Sobald zwischen der Marke und der Wand keine Ziegel mehr liegen, hat Karol diesen Teil abgeschlossen:
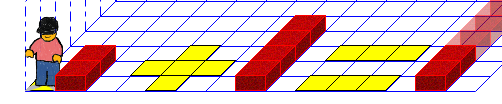
1.4. Zum nächsten Summand
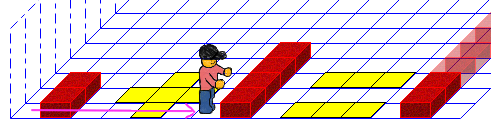
Wir sind mit dem ersten Summanden fertig, können also die Marke löschen und uns vorwärts bewegen.

1.5 Und nochmal markieren

Anderer Stapel, gleiche Prozedur. Wir gehen wie bei 1.2. zum oberen Ende des Stapels und setzen eine Marke.
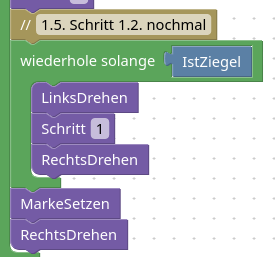
1.6. Und nochmal ins Ergebnis kopieren
Dieser Teil entspricht fast 1-zu-1 dem Abschnitt 1.3. Wichtiger Unterschied sind die Anzahl der Schritte, um beim Ergebnis anzukommen. Du kannst das gesamte "wiederhole" kopieren (Rechtsklick) und wieder einfügen.
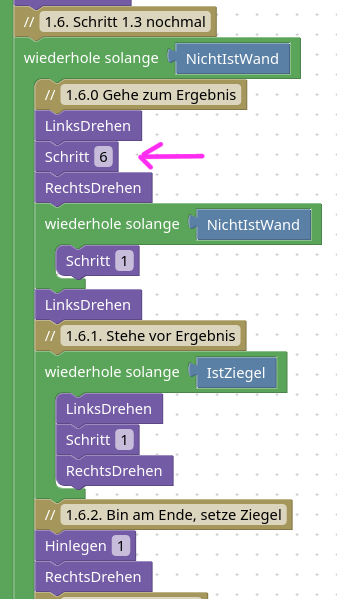
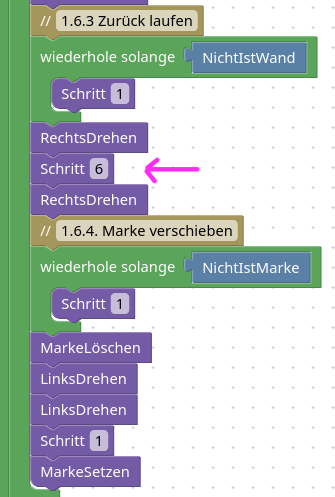
1.7. Abschluss
Jetzt noch die Marke löschen, dann ist die Arbeit getan:

Hier das Ergebnis:

3. Subtraktion
Tja, weil ich lieber die Reihenfolge im Code richtig halten möchte, machen wir jetzt mit der Subtraktion weiter.

Die Rechnung lautet . Glücklicherweise zeige ich dir meine 2. Version, die ich programmiert habe, die um 30 Blöcke kürzer ist als meine erste Version. Das klappt mit folgendem Trick:
3.1. Gehe zu Subtrahend
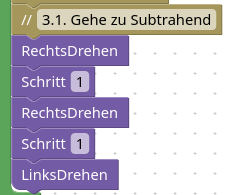
Wir fangen diesmal mit dem 2. Stapel an - im mathematischen Jargon der Subtrahend.
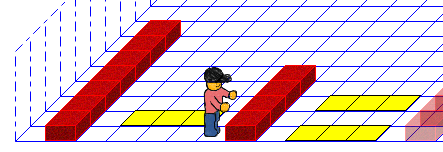
3.2. Gehe zu Ende des Stapels
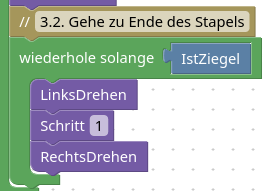
Wir messen wieder den Stapel ab, aber setzen diesmal keine Marke.
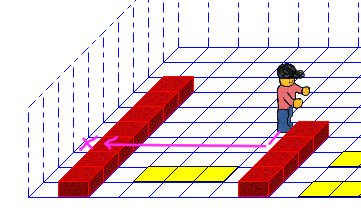
Stattdessen wollen wir im Subtrahend einen Ziegel so setzen, dass wir nur die nötige Anzahl an Ziegel kopieren.
3.3. Markiere im Minuend

Dadurch wird ein Hilfsziegel gelegt. Die Ausgabe zeigt an, dass er eigentlich weg soll - machen wir dann später.

3.4. Gehe zu Start
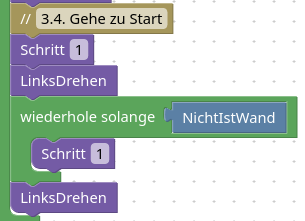
Wir stellen uns in die Ausgangslage.
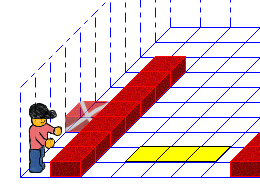
3.5. Markiere Stapel

Ein alter Bekannter. Der Code ist 1-zu-1 der gleiche.

Schaue dir an: zwischen der Marke und dem Ziegel liegen genau 3 freie Felder. Für jedes freie Feld legen wir nun einen Ziegel im Ergebnis.
3.6. Ins Ergebnis kopieren.
Dieser Code verfolgt uns immer wieder. Das gleiche Konstrukt wie in 1.3., nur mit einer anderen Bedingung: Anstatt bis zur Wand zu laufen, laufen wir nur bis zum Ziegel. Der Rest ist 1-zu-1 gleich geblieben.


Und schau mal, das sieht schon mal sehr gut aus.
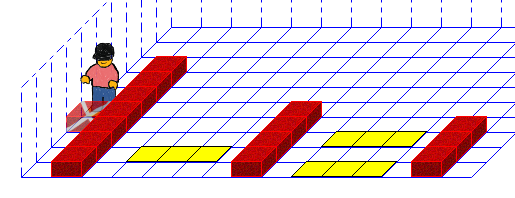
3.7. Aufräumen

Die letzten Sachen noch aufräumen, dann sind wir fertig.
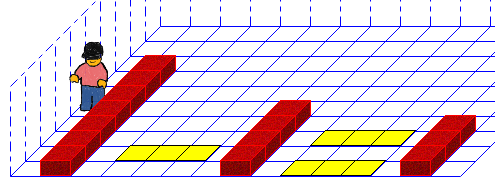
Der Auftrag ist erfolgreich erfüllt. Wir können außerdem davon ausgehen, dass die Subtraktion immer möglich ist, d.h. es kommen keine negativen Zahlen vor.
4. Multiplikation
Immer noch dabei? Wow, Respekt. Als nächstes ist die Multiplikation dran.
4.1. Gehe zu Start

Damit steht Robot Karol für den Auftrag bereit.
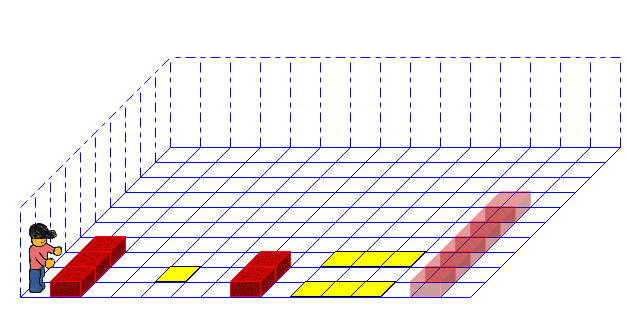
4.2. Markiere Stapel
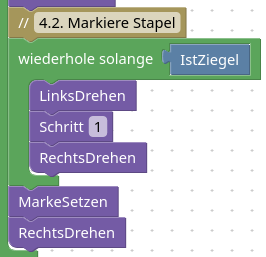
Unser alter Freund.
4.3. Äußere Schleife
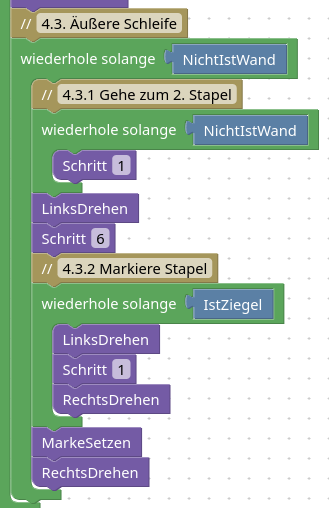
Bei der Addition hat es gereicht, die Stapel nacheinander zu kopieren. Das wird jetzt für die Multiplikation nicht mehr reichen. Wir müssen weiter und noch tiefer verschachteln.

Konkret heißt das jetzt, dass wir in dieser äußeren Schleife nochmal eine Schleife haben werden.
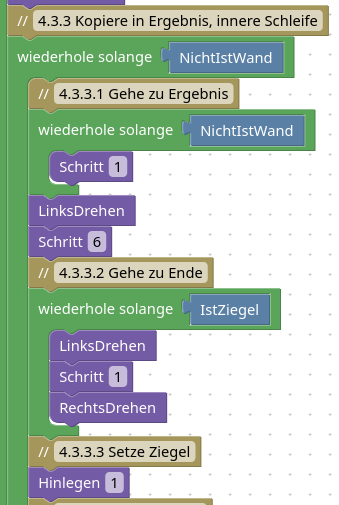

Man muss relativ gut aufpassen, auf welcher Ebene man welche Befehle einfügt. Die innere Schleife 4.3.3. kümmert sich darum, dass der zweite Stapel in das Ergebnis kopiert wird. Das machen wir eben so oft, wie der erste Stapel hoch ist - eine Multiplikation:

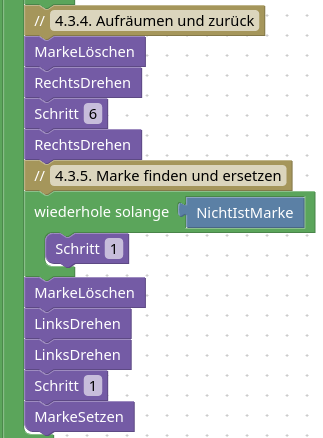
4.4 Aufräumen

Letzte Kleinigkeit, dann ist der Auftrag erfüllt.
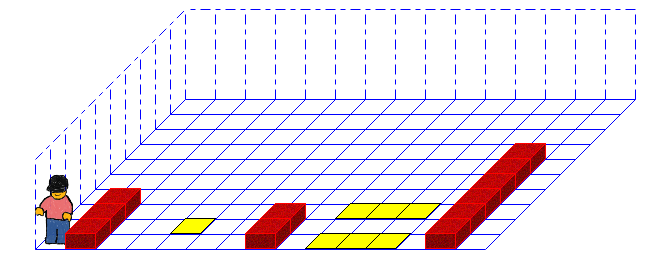
2. Division
Let's go, nur noch eine Rechenart zu erledigen.
2.1. Start
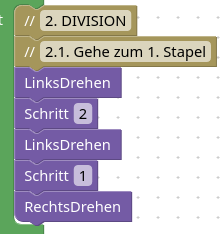
Diesmal starten wir von der anderen Seite. Einfach mal bisschen Abwechslung.
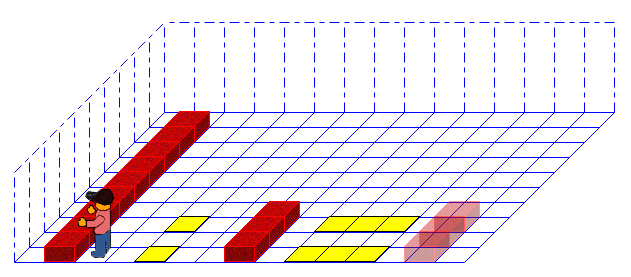
Das Prinzip ist so: Wir wollen solange den 2. Stapel an den ersten Stapel anlegen, bis dieser voll ist. Für jeden Durchlauf zählen wir im Ergebnis 1 hoch. Das tun wir in einer Schleife.
2.2. Äußere Schleife
Achtung, Code-Dump incoming:

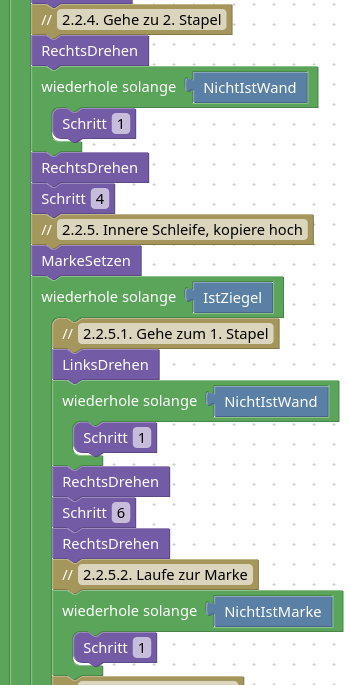

Hier siehst du den Zwischenschritt nach einem Durchlauf.
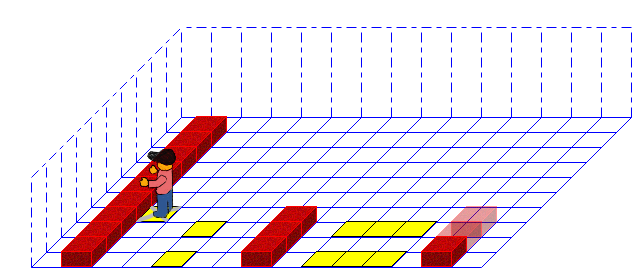
Die gelbe Marke wandert 3 nach oben, im Ergebnis wird 1 hochgezählt. Nach drei Wiederholungen hat Karol die Spitze erreicht und beendet das Programm
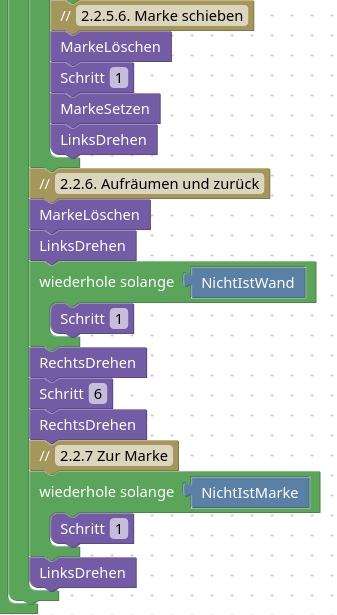
2.3 Aufräumen
Endzustand erreicht.

Zusammenfassung
Nach meiner Zählung sind das 359 Zeilen Code, mit denen wir Robot Karol das Rechnen beigebracht haben. In der Aufgabe findest du noch weitere Testfälle.
Ich hoffe, das war eine lehrreiche und interessante Erfahrung - auch wenn sie sicherlich einiges an Zeit und Gedul erfordert hat.
Bye
