Aufgaben zu Iterationsschemata

1
Berechnung der eulerschen Zahl $e$
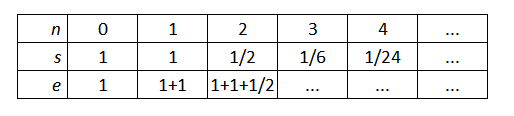
Die folgende Reihe konvergiert gegen die eulersche Zahl $e = 2{,}71828..$ .
1. Stelle ein Iterationsschema für die Berechnung von $e$ auf. Leite daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab. Welche Variablen brauchst du für Zwischenergebnisse? Wie geht der Nenner jeweils eines Bruchs aus dem vorherigen hervor?
  
  Das Iterationsschema stellst du in folgender Weise auf. Du brauchst drei Variablen: $n$ für die Laufvariable des Summenzeichens, $s$ für den jeweiligen Summanden und $e$ für die Summe.
  Aus dem Iterationsschema leitest du die Iterationsgleichungen ab. Eine Variable "mit Strich" bezeichnet den entsprechenden Wert aus der vorhergehenden Spalte.
  $n=n'+1$
  $s = s'/n$
  $e=e'+s$
  Die Werte in der ersten Spalte des Iterationsschemas legst du durch Initialisierung fest.
  $n=0$
  $s=1$
  $e=1$
  Als nächstes formst du diese Gleichungen unmittelbar in ein While-Programm um.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Setze die Iterationsgleichungen in eine While-Schleife um. Brich die While-Schleife ab, wenn der neu hinzugekommene Summand kleiner als $10^{-14}$ ist.
  
  Aus den Iterationsgleichungen und zugehörigen Initialisierungen leitest du die folgende While-Schleife ab.
  n=0 s=1 e=1 while s>1e-14: n+=1 s/=n e+=s
  Die Kurzschreibweise n+=1 bedeutet n=n+1, entsprechend die anderen Kurzschreibweisen s/=n und e+=1. Das Ergebnis ist am Ende der Wert der Variablen $e$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Erstelle unter Benutzung dieser While-Schleife eine Funktion double e() zur Berechnung von $e$ .
2
Berechnung von $\pi$
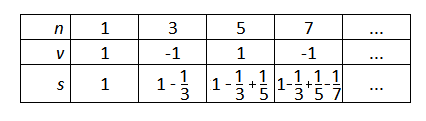
Die Leibniz-Reihe konvergiert (allerdings sehr langsam) gegen den Grenzwert $\pi/4$ :
1. Stelle ein Iterationsschema für die Berechnung von $\pi/4$ auf. Leite daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab.
  
  Das Iterationsschema stellst du in folgender Weise auf. Du brauchst drei Variablen: $n$ für den Nenner, $v$ für das Vorzeichen und $s$ für die Summe.
  Aus dem Iterationsschema leitest du die Iterationsgleichungen ab, .
  $n = n' + 2$
  $v = -v'$
  $s = s' + v/n$
  Die Werte in der ersten Spalte des Iterationsschemas legst du durch Initialisierung fest:
  $n= 1$
  $v = 1$
  $s=1$
  Das war's. Jetzt leitest du daraus unmittelbar ein Programm mit einer While-Schleife ab.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Setze die Ergebnisse aus der vorherigen Teilaufgabe in eine While-Schleife um. Brich die While-Schleife ab, wenn der Wert von $n$ größer oder gleich 10.000 wird.
3. Erstelle unter Benutzung dieser While-Schleife eine Funktion pi() zur (grob angenäherten) Berechnung von $\pi$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zu Iterationsschemata

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?